Eenheidscirkel is een cirkel waarvan de straal 1 is. Het middelpunt van de eenheidscirkel bevindt zich in de oorsprong (0,0) op de as. De omtrek van Unit Circle is 2π eenheden, terwijl de oppervlakte van Unit Circle π eenheden is2. Het heeft alle eigenschappen van Circle. Eenheidscirkel heeft de vergelijking x2+ en2= 1. Deze eenheidscirkel helpt bij het definiëren van verschillende goniometrische concepten.
Eenheidscirkel
De eenheidscirkel wordt vaak aangeduid als S1generalisatie naar hogere dimensies is de eenheidssfeer. Laten we hieronder in detail meer begrijpen over de Unit Circle-, Formula- en Solved-voorbeelden.
Wat is Eenheidscirkel?
Eenheidscirkel is een cirkel met een straal van één (1) eenheid. We gebruiken het cartesische vlak om een eenheidscirkel te tekenen en een eenheidscirkel is een polynoom van 2 graden met twee variabelen. De eenheidscirkel heeft verschillende toepassingen in trigonometrie en algebra en wordt voornamelijk gebruikt om de waarden van verschillende trigonometrische verhoudingen te vinden, zoals sin x, cos x, tan x en andere.
Definitie van de eenheidscirkel
In de wiskunde definiëren we een eenheidscirkel als de meetkundige plaats van een vast punt dat zich op een afstand van één eenheid van het middelpunt van de cirkel bevindt. Een eenheidscirkel heeft een straal van één eenheid en vandaar de naam eenheidscirkel.
Vergelijking van eenheidscirkel
We weten dat de vergelijking van elke cirkel met middelpunt (h, k) en straal ‘r’ is:
(x – h) 2 + (y – k) 2 = r 2
Voor een eenheidscirkel weten we dat r 1 eenheid is en dus is de vergelijking van de eenheidscirkel:
(x – h) 2 + (y – k) 2 = 1
Formule van eenheidscirkel
Als het middelpunt van de eenheidscirkel de oorsprong is, dat wil zeggen (h, k) = (0, 0), dan is de vergelijking van de eenheidscirkel:
X 2 + en 2 = 1
In de onderstaande afbeelding wordt een eenheidscirkel weergegeven, met middencoördinaat h, k en wanneer de cirkel de oorsprong heeft, is de waarde van h en k nul en is de straal AP gelijk aan 1 eenheid.
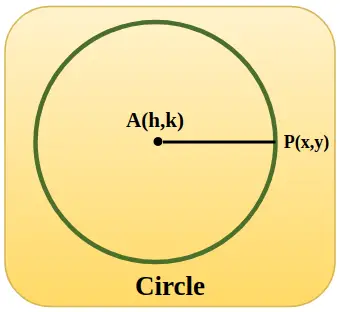
Trigonometrische functies met behulp van eenheidscirkel
De toepassing van de stelling van Pythagoras in een eenheidscirkel kan beter worden gebruikt om trigonometrische functies te begrijpen. Hiervoor beschouwen we een rechthoekige driehoek die binnen een eenheidscirkel in het cartesiaanse coördinatenvlak wordt geplaatst. Als we opmerken, geeft de straal van deze cirkel de hypotenusa van de rechthoekige driehoek aan.
De straal van de cirkel vormt een vector. Dit leidt tot de vorming van een hoek, zeg θ, met de positieve x-as. Laten we aannemen dat x respectievelijk de basislengte is en y de hoogtelengte van de rechthoekige driehoek. Ook zijn de coördinaten van de straalvectoreindpunten respectievelijk (x, y).
De rechthoekige driehoek bevat respectievelijk de zijden 1, x en y. De trigonometrische verhouding kan nu als volgt worden berekend:
sin θ = Hoogte/Hypotenusa = y/1
cos θ = Basis/Hypotenusa = x/1
Nu,
- zonde θ = y
- cos θ = x
- tan θ = sin θ /cos θ = y/x
Door de waarden van θ te vervangen, kunnen we hoofdwaarden van alle trigonometrische functies verkrijgen. Soortgelijke waarden van trigonometrische functies bij verschillende waarden worden gevonden.
Java-arraylist sorteren
Unit Circle met Sin Cos en Tan
Elk punt op de eenheidscirkel met de coördinaten (x, y) wordt weergegeven met behulp van trigonometrische identiteiten als (cosθ, sinθ). De coördinaten van de straalhoeken vertegenwoordigen de cosinus en de sinus van de θ-waarden voor een bepaalde waarde van θ en de straallijn. We hebben cos θ = x, en sin θ = y. Er zijn vier delen van een cirkel die elk in één kwadrant liggen en een hoek vormen van 90°, 180°, 270° en 360°. De straalwaarden liggen respectievelijk tussen -1 en 1. Ook liggen de waarden sin θ en cos θ respectievelijk tussen 1 en -1.
Eenheidscirkel en trigonometrische identiteiten
De trigonometrische identiteiten van de eenheidscirkel voor cotangens, secans en cosecans kunnen worden berekend met behulp van de identiteiten voor sin, cos en tan. Concluderend verkrijgen we een rechthoekige driehoek met respectievelijk de zijden 1, x en y. Het berekenen van de eenheidscirkelidentiteiten kan worden uitgedrukt als:
- zonde θ = y/1
- cos θ = x/1
- bruin θ = y/x
- sec θ = 1/x
- cosec θ = 1/j
- kinderbedje θ = x/y
Eenheidscirkeldiagram
Het eenheidscirkeldiagram is een diagram dat de waarde van de goniometrische functie sinus en cosinus voor verschillende hoeken bevat. Het eenheidscirkeldiagram hiervoor is hieronder toegevoegd,
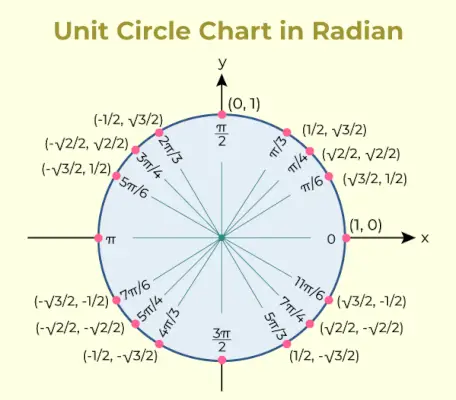
Eenheidscirkeltabel
De trigonometrische verhoudingen die in de eenheidscirkeltabel worden gebruikt, worden gebruikt om de coördinaten te vermelden van de punten op de eenheidscirkel die overeenkomen met gemeenschappelijke hoeken.
| Hoeken | 0° | 30° | 45° | 60° | 90° |
|---|---|---|---|---|---|
| zonder | 0 | 1/2 | 1/√(2) | √3/2 | 1 |
| want | 1 | √3/2 | 1/√(2) | 1/2 | 0 |
| Dus | 0 | 1/√(3) | 1 | √(3) | Niet gedefinieerd conversie van string naar int in java |
| csc | Niet gedefinieerd | 2 | √(2) | 23) | 1 |
| sec | 1 | 23) | √(2) | 2 | Niet gedefinieerd |
| kinderbed | Niet gedefinieerd | √(3) | 1 | 1/√(3) | 0 |
Eenheidscirkel van Pythagoras-identiteiten
Er zijn drie Pythagoras-identiteiten en ze kunnen allemaal gemakkelijk worden bewezen met behulp van het concept van de eenheidscirkel die de drie Pythagoras-identiteiten zijn:
functies in c
- zonder2θ + cos2θ = 1
- 1+zo2θ = sec2i
- 1 + kinderbed2θ = cosec2i
Eenheidscirkel Complex vlak
Complexe getallen en Complex vlak worden eenvoudig uitgelegd met behulp van het concept van de eenheidscirkel. De vergelijking van de eenheidscirkel in complexe vorm is:
|z| = 1
OF
X 2 + en 2 = 1
In de vorm van Euler wordt een complex getal weergegeven als:
z = e Het = cos t + i(sin t)
Lees verder
Opgeloste voorbeelden op Unit Circle
Vraag 1: Bewijs dat punt Q op een eenheidscirkel ligt, Q = [1/√(6), √4/√6]
Oplossing:
Gegeven,
- Q = [1/√(6), √4/√6]
x = 1/√(6), y = √4/√6
Vergelijking van eenheidscirkel is,
X2+ en2= 1
LHS = (1/√(6))2+ (√4/√6)2
LHS = 1/6 + 4/6 = 5/6 ≠ 1
LHS ≠ RHS
Punt Q[1/√(6), √4/√6] ligt dus niet op de eenheidscirkel.
Vraag 2: Bereken zo 30 O met behulp van de sin- en cos-waarden van de eenheidscirkel.
Oplossing:
tan 30° met behulp van sin- en cos-waarden,
bruin 30° = (zonde 30°)/ (cos 30°)
- zonder 30° = 1/2
- cos 30° = √(3)/2
bruin 30° = 1/2/√(3)/2
bruin 30° = 1/√(3)
Vraag 3: Valideer of het punt P [1/2, √(3)/2] op de eenheidscirkel ligt.
Oplossing:
Gegeven,
P = [1/2, √(3)/2]
- x = 1/2
- y = √(3)/2
Vergelijking van eenheidscirkel is,
- X2+ en2= 1
LHS
= (1/2)2+ (√(3)/2)2
= 1/4 + 3/4
= (1 + 3)/4 = 4/4
= 1
= RHS
Oefenvragen op Unit Circle
Q1. Controleer of de punten A (1/2, 3/2) op een eenheidscirkel liggen.
Vraag 2. Controleer of de punten A (2, 1/2) op een eenheidscirkel liggen.
cdr volledige vorm
Q3. Bereken de waarde van cos 240°
Q4. Vind de waarde van bruin 320°
Vraag 5. Vind de waarde van sin 160°
Eenheidscirkel – Veelgestelde vragen
Wat is Eenheidscirkel?
Een eenheidscirkel wordt gedefinieerd als de locatie van een punt dat één eenheid verwijderd is van een vast punt. Het heeft een middelpunt op (0,0) en de waarde van de straal is 1.
Hoe controleer ik of een punt op Unit Circlet ligt?
Elk punt dat in een 2D-vlak ligt en de vorm (x, y) heeft, wordt in de eenheidscirkelvergelijking x geplaatst2+ en2= 1 om te verifiëren of het op de cirkel ligt of niet.
Wat is de formule van Eenheidscirkel?
De eenheidscirkelformule is een formule die wordt gebruikt om een eenheidscirkel algebraïsch weer te geven. De eenheidscirkelformule wordt gegeven als,
X 2 + en 2 = 1
Waarom heet het Unit Circle?
Een eenheidscirkel wordt eenheidscirkel genoemd omdat deze een straal heeft van één (1) eenheden.
