Trigonometrietabel is een standaardtabel die ons helpt de waarden van trigonometrische verhoudingen te vinden voor standaardhoeken zoals 0°, 30°, 45°, 60° en 90°. Het bestaat uit alle zes trigonometrische verhoudingen: sinus, cosinus, tangens, cosecans, secans en cotangens.
Laten we de trigonometrietabel in detail leren kennen.
Inhoudsopgave
- Trigonometrietabel
- Trigonometrische functiestabel
- Truc om trigonometrische verhoudingen te leren
- Hoe trigonometrische tabel te onthouden
- Hoe u een trigtabel maakt
- Trigonometrische formules
- Trigonometrische identiteitstabel
- Trigonometrische tabelvoorbeelden
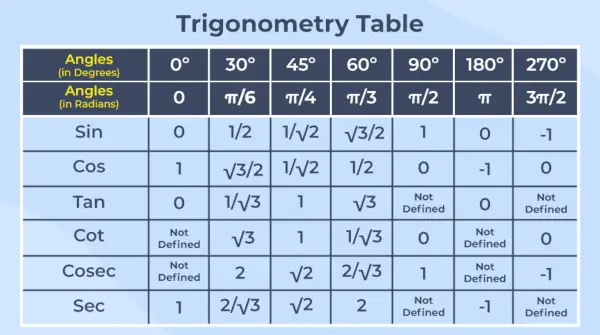
Trigonometrietabel
Trigonometrische tabel is de rangschikking van de waarden van alle zes goniometrische functies voor hun gemeenschappelijke hoeken in tabelvorm.
wat is het internet
Opmerking – Trigonometrie is een tak van de wiskunde die zich bezighoudt met de relaties tussen de hoeken en zijden van rechthoekige driehoeken.
Trigonometrische functiestabel
Trigonometrie heeft 6 basistrigonometrische functies: sinus, cosinus, tangens, cosecans, secans en cotangens. Laten we nu eens kijken naar de trigonometrische functies.
Voor elke rechthoekige driehoek met loodlijn (P), Basis (B) en Hypotenusa (H) zijn de zes trigonometrische functies als volgt:
| Tabel met goniometrische functies | |||
| Functie | Definitie | Vertegenwoordiging | Relatie met zijden van een rechthoekige driehoek |
| Zijn | Verhouding loodrecht en hypotenusa | zonder i | Tegengestelde kant / hypotenusa |
| Cosinus | Verhouding tussen basis en hypotenusa | want i | Aangrenzende zijde / hypotenusa |
| Raaklijn | Verhouding van sinus en cosinus van een hoek | Dus i | Tegenoverliggende zijde/aangrenzende zijde |
| Cosecant | Het omgekeerde van zonde θ | csc i of cosec i | Hypotenusa / tegenoverliggende zijde |
| Secans | Reciproque van cos θ | sec i | Hypotenusa / aangrenzende zijde |
| Cotangens | Reciproque van tan θ | kinderbed i | Aangrenzende zijde / tegenoverliggende zijde |
Opmerking – Trigonometrie is een tak van de wiskunde die zich bezighoudt met de relaties tussen de hoeken en zijden van driehoeken, met name rechthoekige driehoeken. Het omvat de studie en toepassing van sinus-, cosinus-, tangens- en andere trigonometrische functies om problemen op verschillende gebieden op te lossen.
Rekening : Trigonometrie: formules, tabellen, identiteiten en verhoudingen
Truc om trigonometrische verhoudingen te leren
Bestudeer de onderstaande tabel om de trigonometrische verhoudingen op een gemakkelijk te onthouden manier te leren.
| Sommige mensen hebben zwart krullend haar om schoonheid te creëren |
| sin θ (Sommige) = Loodrecht(mensen) / hypotenusa(hebben) |
| cos θ (krullend) = Basis (zwart) / hypotenusa (haar) |
| tan θ (tot) = Loodrecht(produceren) / Basis(schoonheid) |
Hoe trigonometrische tabel te onthouden
Trigonometrietabel is vrij gemakkelijk te onthouden als u alle trigonometrieformules kent. Er is ook een truc genaamd de truc met één hand om de trigonometrietabel te onthouden.

Stap 1: In de bovenstaande afbeelding telt u voor de sinustabel de vingers aan de linkerkant voor de standaardhoek.
Stap 2: Deel het aantal vingers aan de linkerkant (bereken in stap 1) door 4
Stap 3: Zoek de vierkantswortel van de waarde berekend in stap 2.
Rekening: Trigonometrieformules - Lijst met alle trigonometrische identiteiten en formules
Hoe u een trigtabel maakt
Bestudeer de volgende stappen om de goniometrische tabel voor standaardhoeken te maken.
aes versus des
Stap 1: Maak de tabel
Maak een tabel en noteer alle hoeken, zoals 0°, 30°, 45°, 60° en 90°, in de bovenste rij. Voer alle goniometrische functies sin, cos, tan, cosec, sec en cot in de eerste kolom in.
Stap 2: Evalueer de waarde voor alle hoeken van de sinfunctie.
Om de waarden van de sin-functie te vinden, deelt u 0, 1, 2, 3 en 4 door 4 en neemt u onder de wortel van elke waarde, respectievelijk als:
Want de waarde van zonde 0° = √(0/4) = 0
Op dezelfde manier,
zonde 30° = √(1/4) = 1/2
zonde 45° = √(2/4) = 1/√2
zonde 60° = √(3/4) = √3/2
zonde 90° = √(4/4) = 1
| zonder 0° | zonder 30° | zonder 45° | zonder 60° | zonder 90° |
|---|---|---|---|---|
| 0 | 1/2 | 1/√2 | √3/2 | 1 |
Stap 3: Evalueer de waarde voor alle hoeken van de cos-functie
De waarde van de cos-functie is het tegenovergestelde van de waarde van de sin-functie, d.w.z. cos 0° = sin 90°, cos 30° = sin 60° en cos 45° = sin 45°, dus
| cos 0° | cos 30° | cos 45° | cos 60° | cos 90° |
|---|---|---|---|---|
| 1 | √3/2 | 1/√2 | 1/2 | 0 |
Stap 4: Evalueer de waarde voor alle hoeken van de bruiningsfunctie
De waarde van de tan-functie is gelijk aan de sin-functie gedeeld door de cos-functie, d.w.z. tan x = sin x / cos x. De waarde van alle hoeken in de tan-functie wordt berekend als:
tan 0°= sin 0° / cos 0° = 0/1 = 0, op soortgelijke wijze
| dus 0° | dus 30° | dus 45° | dus 60° | dus 90° |
|---|---|---|---|---|
| 0 | 1/√3 | 1 | √3 | Niet gedefinieerd |
Stap 5: Evalueer de waarde voor alle hoeken van de cosec-functie
De waarde van de cosec-functie is gelijk aan het omgekeerde van de sin-functie. De waarde van cosec 0° wordt verkregen door het omgekeerde van sin 0° te nemen
cosec 0° = 1 / sin 0° = 1 / 0 = Niet gedefinieerd. Op dezelfde manier,
| cosec 0° | cosec 30° | cosec 45° | cosec 60° | cosec 90° |
|---|---|---|---|---|
| Niet gedefinieerd | 2 | √2 | 23 | 1 |
Stap 6: Evalueer de waarde voor alle hoeken van de sec-functie
De waarde van de sec-functie is gelijk aan het omgekeerde van de cos-functie. De waarde van sec 0° wordt verkregen door het omgekeerde van cos 0° te nemen
sec 0° = 1 / cos 0° = 1 / 1 = 1. Op dezelfde manier geldt
| seconde 0° | seconde 30° | seconde 45° | seconde 60° | seconde 90° |
|---|---|---|---|---|
| 1 | 23 | √2 | 2 | Niet gedefinieerd |
Stap 7: Evalueer de waarde voor alle hoeken van de wiegfunctie
De waarde van de wiegfunctie is gelijk aan het omgekeerde van de tan-functie. De waarde van cot 0° wordt verkregen door het omgekeerde van tan 0° te nemen
kinderbed 0° = 1 /tan 0° = 1 / 0 = Niet gedefinieerd. Op dezelfde manier,
| kinderbedje 0° | kinderbedje 30° | kinderbedje 45° | kinderbedje 60° | kinderbedje 90° |
|---|---|---|---|---|
| Niet gedefinieerd | √3 | 1 | 1/√3 | 0 |
Op deze manier kunnen we de volgende tabel met trigonometrische verhoudingen maken:
| Graden en radialen trigonometrische tabel | |||||||
|---|---|---|---|---|---|---|---|
| Hoek (in graden) | Hoek (in radialen) | Zonder | Cos | Dus | Cosec | Sec | Kinderbed |
| 0° | 0 | 0 | 1 | 0 | Ongedefinieerd | 1 | Ongedefinieerd |
| 30° | p/6 | 1/2 | √3/2 | 1/√3 | 2 | 23 | √3 |
| 45° | p/4 | √2/2 | √2/2 | 1 | √2 | √2 | 1 |
| 60° | p/3 | √3/2 | 1/2 | √3 | 23 | 2 | 1/√3 |
| 90° | p/2 | 1 | 0 | Ongedefinieerd | 1 | Ongedefinieerd | 0 |
Trigonometrische formules
Laten we enkele trigonometrieformules leren die verband houden met complementaire en aanvullende hoeken.
- Complementaire hoeken: Een paar hoeken waarvan de som gelijk is aan 90°
- Aanvullende hoeken: Een paar hoeken waarvan de som gelijk is aan 180°
Rekening: Trigonometrische verhoudingen
Trig-identiteiten van complementaire hoeken
De identiteit van complementaire hoeken is gebaseerd op de relatie tussen de trigonometrische functies van twee hoeken die samen 90 graden (of π/2 radialen) bedragen. Deze staan bekend als co-functionele identiteiten .
| Trigonometrische functie | Identiteit |
|---|---|
| Zijn | zonde(90°− i )=cos i |
| Cosinus | cos(90°− i )=zonder i |
| Raaklijn | bruin(90°− i )=kinderbed i |
| Cotangens | kinderbed(90°− i )=zo i |
| Secans | sec(90°− i )=csc i |
| Cosecant | cosec(90°− i )=sec i |
Trig-identiteiten van aanvullende hoeken
De identiteiten van aanvullende hoeken hebben betrekking op de trigonometrische functies van twee hoeken die samen 180 graden (of π radialen) bedragen.
| Trigonometrische functie | Identiteit |
|---|---|
| Zijn | zonde(180°− i )=zonder i |
| Cosinus | cos(180°− i )=−cos i |
| Raaklijn | bruin(180°− i )=−bruin i |
| Cotangens | kinderbed(180°− i )=−kinderbed i |
| Secans | sec(180°− i )=−sec i |
| Cosecant | cosec(180°− i )=cosec i |
Trigonometrische identiteitstabel
Trigonometrische identiteiten zijn de identiteiten die veel worden gebruikt bij het oplossen van trigonometrische problemen. Er zijn verschillende trigonometrische identiteiten, maar de drie belangrijkste trigonometrische identiteiten zijn:
| Tabel met trigonometrische identiteiten | |
| Trigonometrische identiteit | Formule |
| Pythagoras identiteit | zonder2θ + cos2θ = 1 |
| Secant-Tangens-identiteit | sec2θ – dus2θ = 1 |
| Cosecant-Cotangente identiteit | cosec2θ – kinderbed2θ = 1 |
Controleer ook:
- Trigonometrische verhoudingen
- Inverse trigonometrische identiteiten
- Hoogten en afstanden
Trigonometrische tabelvoorbeelden
Laten we enkele vragen over de trigonometrische tabel oplossen.
Voorbeeld 1: Als sin θ = 4/5, zoek dan alle trigonometrische waarden.
hoe je een string naar int cast in Java
Oplossing:
Hier hebben we,
zonde θ = 4/5
zoals, zonde θ = Loodrecht / Hypotenusa
dus we hebben Loodrecht (P) = 4 en hypotenusa (H) = 5
Dus volgens de stelling van Pythagoras H 2 = P 2 +B 2
Laten we de waarde van basis (B) achterhalen
52= B2+ 42
25 = B2+ 16
25 -16 = B2
B2= 9
B=3Nu hebben we,
Zonde θ = Loodrecht/Hypotenusa
= AB/AC = 4/5Cosinus θ = Basis/Hypotenusa
= BC/AC = 3/5Raaklijn θ = Loodrecht/Basis
= AB/BC = 4/3Cosecans θ = Hypotenusa/loodrecht
= AC/AB = 5/4Secans θ = hypotenusa/basis
= AC/BC = 5/3slf4j versus log4jCotangens θ = Basis/loodlijn
= BC/AB = 3/4
Voorbeeld 2: Vind de waarde van cos 45° + 2 sin 60° – tan 60°.
Oplossing:
Van de trigonometrietabel,
cos 45° = 1/√2, sin 60° = √3/2 en tan 60° = √3
Dus,
cos 45° + 2 sin 60° – bruin 60° = 1/√2 + 2(√3/2) – √3
= 1/√2
Voorbeeld 3: Vind de waarde van cos 75°.
Oplossing:
We weten dat,
cos 75° = cos (45° + 30°) {as, cos (A + B) = cos A cos B – sin A sin B}
= cos 45° cos 30° – sin 45° sin 30°
= 1/√2 × √3/2 – 1/√2 × 1/2
= (√3 – 1)/2√2cos 75°= (√3 – 1)/2√2.
Conclusie – Trigonometrietabel
De trigonometrietafel biedt een uitgebreide referentie voor de goniometrische functies sinus, cosinus, tangens, cosecans, secans en cotangens, samen met hun respectieve waarden voor verschillende hoeken. I Het dient als een waardevol hulpmiddel bij het oplossen trigonometrische vergelijkingen, het analyseren van geometrische relaties en het begrijpen van het gedrag van periodieke verschijnselen. Of het nu gaat om wiskunde, natuurkunde, techniek of andere vakgebieden, de trigonometrietabel helpt bij berekeningen, probleemoplossing en visualisatie, en draagt bij aan een dieper begrip van trigonometrische concepten en hun toepassingen in scenario's uit de echte wereld.
Trigonometrietabel – Veelgestelde vragen
Wat is trigonometrie?
Trigonometrie is de tak van de wiskunde die zich bezighoudt met de hoek en zijden van elke driehoek.
Wat is een goniometrische tafel?
Trigonometrietabel is een tabel die de waarden bevat van alle zes goniometrische functies voor de gemeenschappelijke hoeken.
Wie heeft de trigonometrietafel uitgevonden?
De Griekse astronoom Hipparchus (127 v.Chr.) vond de trigonometrietafel uit.
Wat zijn standaardhoeken in een goniometrische tabel?
De standaardhoek in een trigonometrische tafel is 0°, 30°, 45°, 60° en 90°
mysql show-gebruikers
Wat is de waarde van bruin 45 graden?
De waarde van bruin 45 graden is 1.
Hoe leer je de trigonometrietafel?
De truc voor het leren van een trigonometrische tabel is:
- Je moet alle waarden van alle hoeken van de zondefunctie leren.
- De waarde van alle hoeken van de cos-functie is het spiegelbeeld van de sin-functie.
- De waarden van de tan-functie kunnen worden berekend door de sin-functie te delen door de cos-functie.
- De waarde van de cosec-functie is omgekeerd evenredig aan sin.
- Op dezelfde manier zijn de sec en cot het omgekeerde van de cos- en cot-functie.
Wat zijn zes basisfuncties in de goniometrische tabel?
De zes trigonometrische basisfuncties in de trigonometrische tabel zijn sinus, cosinus, tangens, secans, cotangens en cosecans.
Zijn er rekenmachines die trigonometrietabellen kunnen vervangen?
Wetenschappelijke rekenmachines kunnen goniometrische verhoudingen voor elke hoek berekenen8.
Wat is het nut van een trigonometrietafel?
De Trigonometrietabel wordt in principe gebruikt om de waarden van alle trigonometrische verhoudingen voor alle hoeken te vinden. Deze waarden hebben een aantal toepassingen in het echte leven.
