Complexe getallen zijn de natuurlijke voortzetting van reële getallen. In de moderne tijd worden complexe getallen op veel gebieden gebruikt, zoals digitale signaalverwerking, cryptografie en veel computergerelateerde velden.

In dit artikel zullen we leren over denkbeeldige getallen, complexe getallen en het type ervan, verschillende bewerkingen op complexe getallen, eigenschappen van complexe getallen, toepassing van complexe getallen, enz.

Definitie van complexe getallen

Complexe getallen zijn de cijfers van het formulier (a + ik b) waar A & B zijn de echte cijfers en i is een denkbeeldige eenheid genaamd jota die √-1 vertegenwoordigt. 2 + 3i is bijvoorbeeld een complex getal waarbij 2 een reëel getal is en 3i een denkbeeldig getal. Complexe getallen kunnen worden geschreven als a + ib, waarbij a en b rationale getallen zijn die kunnen worden weergegeven op een getallenlijn die zich uitstrekt tot oneindigheid .

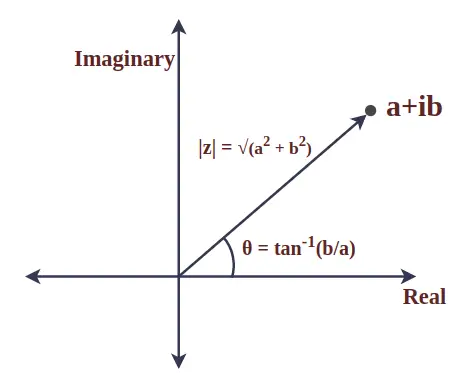
Modulus van complex getal

Modulus van het complexe getal is de absolute waarde en vertegenwoordigt de afstand tussen de oorsprong en het gegeven punt. Het is ook bekend als de grootte van het complexe getal. Laten we een complex getal z = a + ib beschouwen, dan wordt de modulus van z gedefinieerd als:

|z| = √(een ² + b ² )

waar,

• A is het reële deel van het complexe getal z, en
• B is het denkbeeldige deel van het complexe getal z.

Argument van complex getal

De hoek tussen de straalvector van een complex getal en de positieve x-as wordt het argument van een complex getal genoemd. Voor een complex getal z = a + ib wordt het wiskundig gegeven door:

θ = bruin ^-1 (z/a)

waar,

• A is het reële deel van het complexe getal z, en
• B is het denkbeeldige deel van het complexe getal z.

Kracht van i(iota)

De i(iota) wordt gedefinieerd als de vierkantswortel van -1. Elke macht van i kan dus worden uitgedrukt als een herhaalde vermenigvuldiging van i op zichzelf, dat wil zeggen:

• ik = √(-1)
• i²= -1
• i³= – ik
• i⁴= 1
• i⁵= ik
• i⁶= – 1
• enzovoort..

Behoefte aan complexe getallen

In de oudheid hadden mensen alleen kennis van natuurlijke getallen als deze cijfers zijn het meest intuïtief van aard, omdat het menselijk brein ze al begrijpt met behulp van beelden van zaken als schapen en voedsel. We hebben dus alleen de verzameling natuurlijke getallen ( N ) maar in natuurlijke getallen is er geen oplossing voor de vergelijking x + a = b (a> b) en a, b ∈ N. Er ontstond dus een uitbreiding van natuurlijke getallen, d.w.z. gehele getallen( I ).

Ook in deze reeks getallen is er geen oplossing voor de vergelijking ax = b (a ≠ 0) en a, b ∈ I, waarbij a en b beide gehele getallen zijn. Een reeks gehele getallen (I) wordt dus uitgebreid tot een reeks rationale getallen ( Q ).

Nogmaals, in deze reeks rationale getallen is er geen oplossing voor de vergelijking x²= a (a> 0) en a ∈ Q. Dus Q wordt uitgebreid met getallen zodat x²= a(voor a> 0), dat wil zeggen, irrationele getallen. Deze set heet Real Numbers en wordt vertegenwoordigd door R .

Lange tijd werd gedacht dat we deze reeks reële getallen niet hoeven uit te breiden om nog een grotere reeks te vormen, omdat deze verzameling getallen compleet lijkt. Maar opnieuw ontstond er een nieuw probleem in deze reeks getallen, d.w.z. er is geen reëel getal zo groot als x²= a (a <0) en a ∈ R. De reeks reële getallen wordt dus verder uitgebreid met al deze gewaardeerde en genoemde complexe getallen en wordt weergegeven door C .

Classificatie van complexe getallen

Zoals we weten is de standaardvorm van een complex getal: z = (a + ik b) waarbij a, b ∈ R en i iota zijn (een denkbeeldige eenheid). Dus afhankelijk van de waarden van a (het zogenaamde reële deel) en b (het imaginaire deel genoemd), worden de complexe getallen ingedeeld in vier typen:

• Nul complex getal
• Puur echte cijfers
• Puur denkbeeldige getallen
• Denkbeeldige getallen

Laten we deze typen in detail leren kennen.

Nul complex getal

Voor elk complex getal z = a + ib als a = 0 en b = 0, wordt het complexe getal nul complex getal genoemd. Het enige voorbeeld hiervan is bijvoorbeeld 0.

Puur echte cijfers

Voor elk complex getal z = a + ib als a ≠ 0 & b = 0, dan wordt het complexe getal een puur reëel getal genoemd, dat wil zeggen een getal zonder denkbeeldig deel. Alle reële getallen zijn hiervan voorbeelden, zodat 2, 3, 5, 7, enz.

Puur denkbeeldige getallen

Voor elk complex getal z = a + ib als a = 0 & b ≠ 0, dan wordt een complex getal een puur denkbeeldig getal genoemd, dat wil zeggen een getal zonder reëel deel. Alle getallen zonder echte delen zijn voorbeelden van dit type getallen, dat wil zeggen -7i, -5i, -i, i, 5i, 7i, enz.

Denkbeeldige getallen

Voor elk complex getal z = a + ib als a ≠ 0 & b ≠ 0, dan wordt een complex getal an genoemd denkbeeldig getal . Bijvoorbeeld (-1 – i), (1 + i), (1 – i), (2 + 3i), enz.

Verschillende vormen van complexe getallen

Er zijn verschillende vormen van complexe getallen die,

• Rechthoekige vorm
• Polaire vorm
• Exponentiële vorm

Laten we ze nu in detail leren kennen.

Rechthoekige vorm

Rechthoekige vorm is ook wel genoemd Standaard vorm en het wordt vertegenwoordigd door (a + ib), waarbij a en b de reële getallen zijn.

Bijvoorbeeld: (5 + 5i), (-7i), (-3 – 4i), enz.

Polaire vorm

Polaire vorm is de representatie van een complex getal waarbij poolcoördinaten [waarbij coördinaten worden weergegeven als (r, θ), waarbij r de afstand vanaf de oorsprong is en θ de hoek is tussen de lijn die het punt en de oorsprong verbindt en de positieve x-as) worden gebruikt om een ​​complex getal weer te geven. Elk complex getal wordt weergegeven als r [cos θ + ik zonde θ].

Bijvoorbeeld: [cos π/2 + i sin π/2], 5[cos π/6 + i sin π/6], enz.

Exponentiële vorm

Exponentiële vormen van complexe getallen is de weergave van complexe getallen met behulp van de formule van Euler en in deze vorm wordt een complex getal weergegeven door reⁱ, waarbij r de afstand is van een punt tot de oorsprong en θ de hoek is tussen de positieve x-as en de straalvector.

Voor voorbeelden: e^ik(0), Het is^ik(π/2), 5.e^ik(π/6), enz.

Opmerking: Alle drie de hierboven besproken vormen van de complexe getallen zijn onderling converteerbaar, dat wil zeggen dat ze heel gemakkelijk van de ene vorm naar de andere kunnen worden omgezet.

Bewerkingen op complexe getallen

De volgende bewerkingen kunnen worden uitgevoerd op complexe getallen:

• Toevoeging
• Aftrekken
• Vermenigvuldiging
• Divisie
• Conjugatie

Optelling van complexe getallen

We kunnen twee complexe getallen optellen door simpelweg hun reële en imaginaire delen afzonderlijk op te tellen.

Bijvoorbeeld (3 + 2i) + (1 + 4i) = 4 + 6i.

Aftrekken van complexe getallen

We kunnen twee complexe getallen aftrekken door simpelweg hun reële en imaginaire delen afzonderlijk af te trekken.

Bijvoorbeeld (3 + 2i) – (1 + 4i) = 2 – 2i.

Vermenigvuldiging van complexe getallen

We kunnen twee complexe getallen vermenigvuldigen met behulp van de distributieve eigenschap en het feit dat i²= -1.

Bijvoorbeeld (3 + 2i)(1 + 4i) = 3 + 12i + 2i + 8i²= 3 + 14i – 8 = -5 + 14i.

Deling van complexe getallen

We kunnen het ene complexe getal door het andere delen, door simpelweg zowel de teller als de noemer te vermenigvuldigen met de complexe conjugaat van de noemer en de uitdrukking verder te vereenvoudigen.

Bijvoorbeeld (3 + 2i)/(1 + 4i) = (3 + 2i)(1 – 4i)/(1 + 4i)(1 – 4i) = (11 – 10i)/17.

Vervoeging van complexe getallen

Wij kunnen de conjugaat van een complex getal, door simpelweg het teken van het denkbeeldige deel ervan te veranderen. Een conjugaat van een complex getal wordt vaak aangegeven met een balk boven het getal, zoals z̄.

Het conjugaat van 3 + 2i is bijvoorbeeld 3 – 2i.

Identiteiten voor complexe getallen

Voor twee complexe getallen z₁en z₂de volgende algebraïsche identiteiten kunnen worden gegeven:

• (Met ₁ + z ₂ ) ² = (z ₁ ) ² + (z ₂ ) ² + 2 z ₁ × z ₂
• (Met ₁ - Met ₂ ) ² = (z ₁ ) ² + (z ₂ ) ² – 2z ₁ × z ₂
• (Met ₁ ) ² - (Met ₂ ) ² = (z ₁ + z ₂ )(Met ₁ - Met ₂ )
• (Met ₁ + z ₂ ) ³ = (z ₁ ) ³ + 3(z ₁ ) ² Met ₂ +3(z ₂ ) ² Met ₁ + (z ₂ ) ³
• (Met ₁ - Met ₂ ) ³ = (z ₁ ) ³ – 3(z ₁ ) ² Met ₂ +3(z ₂ ) ² Met ₁ - (Met ₂ ) ³

Formules gerelateerd aan complexe getallen

Er zijn enkele formules gerelateerd aan complexe getallen, waarvan sommige als volgt zijn:

Eulers formule

De formule van Euler toont de relatie tussen de denkbeeldige macht van exponent en de trigonometrische verhouding sin en cos en wordt gegeven door:

Het is ^ix = cos x + ik zonde x

De formule van De Moivre

De formule van De Moivre drukt de n uit^emacht van een complex getal in polaire vorm en wordt gegeven door:

(omdat x + ik zonde x) ^N = cos(nx) + ik zonde(nx)

Complex vliegtuig

Het vlak waarop de complexe getallen op unieke wijze worden weergegeven, wordt het complexe vlak, het Argand-vlak of het Gauss-vlak genoemd.

Het complexe vlak heeft twee assen:

• X-as of echte as
• Y-as of denkbeeldige as

X-as of echte as

• Alle puur reële complexe getallen worden op unieke wijze weergegeven door een punt erop.
• Het reële deel Re(z) van alle complexe getallen wordt ten opzichte daarvan uitgezet.
• Daarom wordt de X-as ook wel genoemd Echte as .

Y-as of denkbeeldige as

• Alle puur denkbeeldige complexe getallen worden op unieke wijze weergegeven door een punt erop.
• Het denkbeeldige deel Im(z) van alle complexe getallen wordt ten opzichte daarvan uitgezet.
• Daarom wordt de Y-as ook wel genoemd Denkbeeldige as .

Geometrische weergave van complexe getallen

Zoals we weten, wordt elk complex getal (z = a + i b) weergegeven door een uniek punt p(a, b) op het complexe vlak en vertegenwoordigt elk punt op het complexe vlak een uniek complex getal.

Om elk complex getal z = (a + i b) op het complexe vlak weer te geven, volgt u deze conventies:

• Het reële deel van z (Re(z) = a) wordt de X-coördinaat van het punt p

• Het denkbeeldige deel van z (Im(z) = b) wordt de Y-coördinaat van het punt p

En tenslotte z (a + i b) ⇒ p (a, b), wat een punt op het complexe vlak is.

Eigenschappen van complexe getallen

Er zijn verschillende eigenschappen van complexe getallen, waarvan sommige als volgt zijn:

• Voor elk complex getal z = a + ib, als z = 0, dan geldt zowel a = 0 als b = 0.
• Voor 4 reële getallen a, b, c en d zodat z₁= a + ib en z₂= c + identiteitskaart. Als z₁= z₂dan a = c, en b = d.
• Optelling van een complex getal met zijn conjugaat resulteert in een puur reëel getal, dat wil zeggen z + z̄ = reëel getal.

Laat z = a + ib,

z + z̄ = a + één + a – één

⇒ z + z̄ = 2a (wat puur reëel is)

• Het product van een complex getal met zijn geconjugeerde resultaten is ook een puur reëel getal, dwz z × z̄ = reëel getal

Stel dan z = a + ib

z × z̄ = (a + één) × (a – één)

azuur abonnement

⇒ z × z̄= a²- i²B²

⇒ z × z̄ = a²+ b²(wat puur echt is)

• Complexe getallen zijn dat wel commutatief onder de werking van optellen en vermenigvuldigen. Laten we twee complexe getallen z beschouwen₁en z₂, en dan

Met ₁ +z ₂ = z ₂ +z ₁

Met ₁ × z ₂ = z ₂ × z ₁

• Complexe getallen zijn dat wel associatief met de bewerking van optellen en vermenigvuldigen. Laten we drie complexe getallen z bekijken₁, Met₂, en z₃Dan

(Met ₁ +z ₂ ) +z ₃ = z ₁ + (z ₂ +z ₃ )

(Met ₁ ×z ₂ )×z ₃ = z ₁ ×(z ₂ ×z ₃ )

• Complexe getallen houden de distributieve eigendom ook van vermenigvuldigen boven optellen. Laten we drie complexe getallen z bekijken₁, Met₂, en z₃Dan

Met ₁ ×(z ₂ +z ₃ ) = z ₁ ×z ₂ + z ₁ ×z ₃

Lees verder,

• Complexe getallen delen
• Z-balk in complexe getallen

Voorbeelden van complexe getallen

Voorbeeld 1: Teken deze complexe getallen z = 3 + 2i op het complexe vlak.

Oplossing:

Gegeven:

Met = 3 + 2 ik

Het punt is dus z(3, 2). Nu zetten we dit punt uit in de onderstaande grafiek. Hier in deze grafiek vertegenwoordigt de x-as het reële deel en de y-as het denkbeeldige deel.

Voorbeeld 2: Teken deze complexe getallen z ₁ = (2 + 2 ik), z ₂ = (-2 + 3 ik), z ₃ = (-1 – 3 i), z ₄ = (1 – i) op ​​het complexe vlak.

Oplossing:

Gegeven:

Met₁= (2 + 2 ik)

Met₂= (-2 + 3 ik)

Met₃= (-1 – 3 ik)

Met₄= (1 – ik)

De punten zijn dus z₁(2, 2), z₂(-2, 3), z₃(-1, -3) en z₄(1, -1). Nu zetten we deze punten uit in de onderstaande grafiek. Hier in deze grafiek vertegenwoordigt de x-as het reële deel en de y-as het denkbeeldige deel.

Veelgestelde vragen over complexe getallen

Definieer complexe getallen.

Getallen van de vorm a+ib worden complexe getallen genoemd, waarbij a en b het reële getal zijn en i de denkbeeldige eenheid is die de vierkantswortel van -1 vertegenwoordigt.

Wat is het verschil tussen een reëel getal en een complex getal?

Het verschil tussen reële en complexe getallen is dat we slechts één getal nodig hebben om een ​​reëel getal weer te geven, maar twee reële getallen om een ​​complex getal weer te geven.

Wat is het reële deel en het imaginaire deel van een complex getal?

In een complex getal a + ib is a het reële deel van het complexe getal, en wordt b het imaginaire deel van het complexe getal genoemd.

Wat is de complexe conjugaat van een complex getal?

Voor een complex getal a + ib wordt a – ib het complexe conjugaat ervan genoemd. Complexe conjugaten kunnen worden gevonden door simpelweg het teken van het denkbeeldige deel te veranderen.

Wat is de modulus van een complex getal?

De afstand tussen de oorsprong en het punt dat wordt weergegeven door een complex getal in het argandvlak wordt de modulus van dat volledige getal genoemd en voor z = a + ib wordt deze wiskundig gegeven door:

|z| = √(een ² + b ² )

Wat is het argument van een complex getal?

De hoek tussen de straalvector van een complex getal en de positieve x-as wordt het argument van een complex getal genoemd en voor z = a + ib wordt deze wiskundig gegeven door:

θ = bruin ^-1 (z/a)

Wat is de polaire vorm van een complex getal?

Voor elk complex getal, z = a + ib, wordt de polaire vorm hiervan gegeven door:

r [cos θ + ik zonde θ]

Wat is de formule van Euler?

De formule van Euler toont de relatie tussen de denkbeeldige macht van exponent en de trigonometrische verhouding sin en cos en wordt gegeven door:

Het is ^ix = cos x + ik zonde x