de Cosinus-functie of de want functie is kortweg een van de zes Trigonometrische functies fundamenteel voor trigonometrie. Cosinus in trigonometrie wordt gegeven als de verhouding van de basis tot de hypotenusa van een rechthoekige driehoek. De cosinusfunctie wordt weergegeven als Cos x waarbij x de hoek is waarvoor de cosinusverhouding wordt berekend. In termen van functie kunnen we zeggen dat x de invoer of het domein van de cosinusfunctie is.
Het wordt op grote schaal gebruikt in een breed scala aan onderwerpen, zoals natuurkunde, meetkunde en techniek, onder andere door gebruik te maken van het periodieke karakter ervan. Het wordt bijvoorbeeld gebruikt om de golfkarakteristiek van geluidsgolven te definiëren, berekeningen van de elektrische flux door een vlak oppervlak, enz. In dit artikel leren we in detail over wat de cosinusfunctie is, de Domein en bereik van de cosinusfunctie, de periode en de grafiek van de cosinusfunctie.
Inhoudsopgave
- Wat is de cosinusfunctie?
- Cos in eenheidscirkel
- Cosinusfunctiegrafiek
- Inverse van cosinusfunctie
- Cosinusfunctie in Calculus
- Cos-functie-identiteiten
Wat is de cosinusfunctie?
Cosinusfunctie is een trigonometrische functie die in principe periodiek van aard is. De cosinusfunctie wordt uitgedrukt als cos x waarbij x een van de scherpe hoeken van een rechthoekige driehoek is. Cosinusfunctie vindt de verhouding tussen basis en hypotenusa voor een gegeven waarde van x. De cosinusfunctie wordt afgekort als cos(x) of cos(θ), waarbij x de hoek in radialen is en theta θ de hoek in graden over het algemeen. De cosinusfunctie kan worden gedefinieerd met behulp van een eenheidscirkel, dat wil zeggen een cirkel met een straaleenheid, zoals we later in dit artikel zullen zien. Het is periodiek van aard en herhaalt zijn waarden na elke volledige rotatie van hoeken. Op een cartesisch vlak kan er naar worden verwezen als de vectorcomponent van de hypotenusa evenwijdig aan de x-as.
Cosinusfunctiedefinitie
De cosinusfunctie wordt in een rechthoekige driehoek gedefinieerd als de verhouding tussen de lengte van de zijde grenzend aan de betreffende hoek en de lengte van de hypotenusa. Wiskundig gezien wordt de cosinusfunctie gegeven als
Cos x = Cos θ = Lengte van basis/lengte van hypotenusa = b/h = OB/OA
waar X is de hoek in radialen en θ is de equivalente hoek in graden.
Domein en bereik van Cos-functie
We weten dat voor een functie domein de toegestane invoerwaarden zijn en bereik de uitvoerwaarde voor die specifieke invoer- of domeinwaarde. Daarom kunnen we aannemen dat de functie fungeert als een processor die invoer ontvangt, verwerkt en bepaalde uitvoer geeft. Het domein en het bereik van de cos-functie worden hieronder besproken:
- Domein van cosinusfunctie: R dat wil zeggen, een verzameling van alle reële getallen.
- Bereik van cosinusfunctie: [-1, 1], d.w.z. de uitvoer varieert tussen alle reële getallen tussen -1 en 1.
Periode van een cosinusfunctie
De functie is periodiek van aard, dat wil zeggen dat het zichzelf herhaalt na 2π of 360°. Met andere woorden, het herhaalt zichzelf na elke volledige rotatie. Daarom is de periode van de cosinusfunctie een volledige rotatie of een hoek van 360 ° (of 2π).
Reciproque van een cosinusfunctie
Het omgekeerde van een cosinusfunctie staat bekend als secans functie of sec in het kort. Wiskundig gezien wordt het omgekeerde van de cosinusfunctie gegeven als
Java is leeg
sec(θ) = 1/cos(θ)
Volgens de regels van wederkerigheid Als we Cos x vermenigvuldigen met Sec x, is het product altijd 1.
Cosinusfunctiegrafiek
De grafiek van de cosinusfunctie lijkt op de grafiek van de sinusfunctie met het fundamentele verschil dat voor x = 0 de sinfunctiegrafiek van de oorsprong loopt, terwijl bij x = 0 de cosinusfunctiegrafiek van (0, 1) naar y-aixs gaat. Hieronder volgt de grafiek van de waarde van de cosinusfunctie, dwz y = cos x
De hierboven besproken eigenschappen zijn in de grafiek te zien, zoals de periodieke aard van de functie.
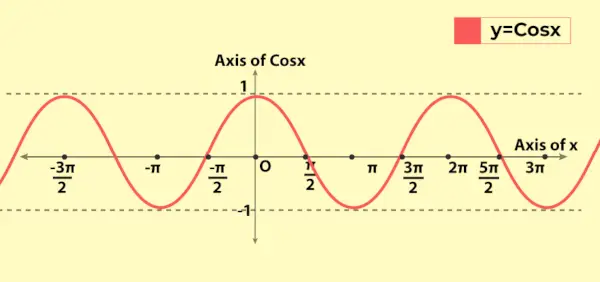
Variatie van cosinusfunctie in grafiek
Omdat het bereik van de cosinusfunctie [-1, 1] is, varieert het daarom van -1 tot 1 in de grafiek. Het vertoont zijn periodieke karakter, aangezien de grafiek zich herhaalt na elke lengte 2π op de x-as. Dit weerspiegelt dat de cosinusfunctie een periode van 2π (of 360°) heeft.
Cos in eenheidscirkel
De cosinusfunctie kan worden gedefinieerd met behulp van de eenheidscirkel. Laten we begrijpen hoe we de cosinusfunctie kunnen definiëren in termen van eenheidscirkel.

Beschouw een lijnstuk OA dat roteert om het punt O, waar O de oorsprong is van het cartesische vlak. De rotatie van OA beschrijft dus een eenheidscirkel (cirkel met eenheidsstraal) gecentreerd op de oorsprong O en het punt A ligt altijd op deze cirkel. Als we een loodlijn van A op de x-as laten vallen en het snijpunt B noemen, en θ de hoek is die OA maakt met de positieve richting van de x-as, dan is cos(θ) = projectie van de hypotenusa op x -as = OB/|OA| = OB (sinds |OA| = 1 eenheid).
Merk op dat de richting OB belangrijk is, zoals te zien is in de volgende afbeeldingen. Het groene segment geeft de lengte/grootte aan en de pijl geeft de richting (+ve of -ve) van cos(θ) aan

Merk op dat de waarde van cos(θ) positief is voor θ behorend tot het eerste en vierde kwadrant, terwijl negatief voor θ behorend tot het tweede en derde kwadrant.
Inverse van cosinusfunctie
De inverse van een cosinusfunctie die bekend staat als boog-cosinus functie en afgekort als arccos(x) of want -1 (X) wordt als volgt gedefinieerd
cos(x) = y
⇒ cos -1 (j) = x
Domein en bereik van inverse cosinusfunctie
Het domein en bereik van de inverse cosinusfunctie worden hieronder vermeld:
- Domein van inverse cosinusfunctie: Alle reële getallen binnen bereik [-1, 1]
- Bereik van inverse cosinusfunctie: Alle reële getallen binnen bereik [0, π]
Hyperbolische cosinusfunctie
Hyperbolische functies zijn een analoog equivalent van de trigonometrische functie waarvan de algebraïsche uitdrukking in termen van exponentiële functie is. De hyperbolische cosinusfunctie afgekort als cosh(x) waar X is een hyperbolische hoek is een concept van hyperbolische meetkunde. Zoals (cos(x), sin(x)) een punt op een eenheidscirkel vertegenwoordigt, vertegenwoordigt (cosh(x), sinh(x)) een punt op een eenheidshyperbool, d.w.z. xy = 1 waarbij sinh(x) hyperbolisch vertegenwoordigt sinus functie. De algebraïsche uitbreiding van de hyperbolische cos-functie wordt gegeven als
cosh(x) = (bijv X + en -X )/2
Meer details over hyperbolische functies vallen buiten het bestek van dit artikel, maar u kunt hiernaar verwijzen Dit artikel .
Cosinusfunctie in Calculus
De tak van de calculus in de wiskunde houdt zich bezig met de differentiatie en integratie van een bepaalde functie. Differentiatie van de functie is de snelheid waarmee de functie verandert ten opzichte van de onafhankelijke variabele, terwijl integratie het omgekeerde proces van differentiatie is dat zich bezighoudt met het vinden van de integraal van een functie waarvan de afgeleide bestaat.
Afgeleide van cosinusfunctie
De derivaat van de cosinusfunctie is gelijk aan het negatief van de sinusfunctie. Wiskundig
d(cos(x))/dx = -sin(x)
Integratie van cosinusfunctie
De onbepaalde integraal van de cosinusfunctie is gelijk aan de sinusfunctie. Wiskundig –
∫cos(x)dx = sin(x) + C, waarbij C de integratieconstante is.
Sinus- en cosinusfuncties
De volgende grafiek geeft het belangrijkste verschil weer tussen zowel de sinus- als de cosinusfunctie:

Verschil tussen sinus- en cosinusfuncties
De volgende tabel geeft een overzicht van de verschillen tussen de sinus- en cosinusfunctie -
Sinus-functie | Cosinus-functie |
|---|---|
In een eenheidscirkel is de sinus van een hoek de projectie van de hypotenusa op de y-as. | In een eenheidscirkel is de cosinus van een hoek de projectie van de hypotenusa op de x-as. |
sin(θ) = Hoogte van de rechthoekige driehoek / Lengte van de hypotenusa | cos(θ) = Basis van de rechthoekige driehoek / Lengte van de hypotenusa |
De waarde is 0 bij 0°, 180° en 360°. | De waarde is 0 bij 90° en 270°. |
De waarde ervan is maximaal, d.w.z. 1 bij 90°. | De waarde ervan is maximaal, d.w.z. 1 bij 0° en 360°. |
De waarde ervan is minimaal, d.w.z. -1 bij 270°. | De waarde ervan is minimaal, d.w.z. -1 bij 180°. |
Cos-waardetabel
De volgende tabel geeft de waarden van de cosinusfunctie voor enkele veel voorkomende hoeken in het eerste kwadrant van het cartesiaanse vlak -
Hoek in graden (θ) | Hoek in radialen (x) | Cos (x) |
|---|---|---|
0 | 0 | 1 |
30 | p/6 | √3/2 |
Vier vijf | p/4 | 1/√2 |
60 | p/3 | 1/2 |
90 | p/6 | 0 |
We kunnen eenvoudig de waarden van andere veel voorkomende hoeken berekenen, zoals 15°, 75°, 195°, -15°, etc. met behulp van deze waarden door de formules cos (x + y) en cos (x – y) te gebruiken die verderop in dit boek worden beschreven. artikel.
Rekening, Trigonometrische tabel
Cos-functie-identiteiten
De fundamentele trigonometrische identiteiten gerelateerd aan de cosinusfunctie worden hieronder vermeld:
- zonder2(x) + cos2(x) = 1
- cos(x + y) = cos(x)cos(y) – sin(x)sin(y)
- cos(x – y) = cos(x)cos(y) + sin(x)sin(y)
- cos(-x) = cos(x)
- cos(x) = 1/sec(x)
- cos 2x = cos2x – zonde2x = 1 – 2sin2x = 2cos2x – 1 = (1 – bruin2x/1 + bruin2X)
- cos 3x = 4cos3x – 3cos x
gerelateerde artikelen
- Differentiatie van goniometrische functies
- Inverse trigonometrische functies
- Inverse Trig-derivaten
Opgeloste voorbeelden van cosinusfunctie
Hier zijn enkele opgeloste voorbeelden om u te helpen het concept van de cosinusfunctie beter te begrijpen.
Voorbeeld 1: Wat zijn de maximale en minimale waarden van de cosinusfunctie?
Oplossing:
De maximale waarde van de cosinusfunctie is 1 bij 0° en 180°, terwijl de minimumwaarde van de functie -1 is bij 180°.
Voorbeeld 2: Onder welke hoek(en) in het bereik [0, 360] is de waarde van de cosinusfunctie 0?
Oplossing:
De waarde van de cosinusfunctie is 0 bij de hoeken 90° en 270°.
Voorbeeld 3: Voor welke kwadranten is de waarde van de cosinusfunctie negatief?
Oplossing:
De cosinusfunctie is negatief in IInlen IIIrdkwadranten.
Voorbeeld 4: Bereken de waarde van cos (45°).
Oplossing:
subtekenreeks java
Volgens identiteit 4 hierboven gegeven, cos(-x) = cos(x).
Daarom geldt cos(-45°) = cos(45°) = 1/√2
Voorbeeld 5: Bereken de waarde van cos(15°).
Oplossing:
Met behulp van identiteit 3 hierboven gegeven -
cos(15degree) = cos(45degree – 30degree) ewline = cos(45degree)cos(30degree) + sin(45degree)sin(45degree) ewline = frac{1}{sqrt2} imesfrac{sqrt3}{2} + frac{1}{sqrt2} imes frac{1}{2} ewline = frac{sqrt3 + 1}{2sqrt2}
Voorbeeld 6: Wat is cos -1 (1/2) in het bereik [0,π]?
Oplossing:
Laat cos-1(1/2) = j.
Daarom cos(y) = 1/2 ⇒ y = π/3 in het hierboven gegeven bereik.
Het antwoord is dus π/3.
Voorbeeld 7: Wat is de waarde van cos(-15°)?
Oplossing:
Met behulp van de hierboven gegeven identiteit 3 -
cos(-15degree) ewline = cos(30degree – 45degree) ewline = cos(30degree)cos(45degree) + sin(30degree)sin(45degree) ewline = frac{sqrt3}{2} imesfrac{1}{sqrt{2}} + frac{1}{2} imesfrac{1}{sqrt2} ewline = frac{sqrt3 + 1}{2sqrt2} .Als alternatief kunnen we ook de identiteit cos(-x) = cos(x) gebruiken en de waarde van cos(15°) gebruiken, berekend in voorbeeld 5.
Voorbeeld 8: Bereken de oppervlakte onder de grafiek van de cosinusfunctie voor x = 0 tot x = π/2.
Oplossing:
Het gegeven gebied kan worden berekend door de volgende definitieve integraal op te lossen:
int_0^{frac{pi}{2}}cos(x)dx ewline = sin(frac{pi}{2}) – sin(0) ewline = 1 – 0 ewline = 1 Het antwoord is daarom 1 vierkantseenheid.
Voorbeeld 9: Als cos(x) = π/3, zoek dan de waarde van cos(3x) (in decimale vorm met een precisie van twee decimalen).
Oplossing:
Gebruikmakend van de identiteit – cos(3x) = 4cos3(x) – 3cos(x) –
cos(3x) = 4⨉(π/3)3-3⨉(π/3) ≅ 4,59 – π = 1,45
Voorbeeld 10: Vind de waarde van cos(120°).
Oplossing:
De identiteit gebruiken voor cos(2x)
cos(120°) = cos(2⨉60°) = 1 – 2 sin2(60°) = 1- 2⨉(√3/2)2= 1 – 3/2 = -1/2
Oefenvragen: Cos-functies
Q1. Wat is de formule om de cos van een hoek in een rechthoekige driehoek te berekenen?
Vraag 2. Wat is de geometrische interpretatie van cos op het cartesiaanse vlak?
Q3. Bereken de waarde van cos(120°).
Q4. Bereken de waarde van cos -1 (√3/2) in het bereik [π, 2π].
Vraag 5. Als een paal een schaduw van dezelfde lengte op de grond werpt, zoek dan de hoek van de zon ten opzichte van de grond als de zon in oostelijke richting staat.
Samenvatting - Cosinusfunctie
De cosinusfunctie, aangeduid als cos(x), is een fundamentele trigonometrische functie die wordt gedefinieerd als de verhouding van de basis tot de hypotenusa in een rechthoekige driehoek en is vanwege zijn periodieke aard essentieel in verschillende vakgebieden, zoals natuurkunde, techniek en meetkunde. , wat een belangrijke rol speelt bij het modelleren van golfgedrag. Het heeft een domein van alle reële getallen en een bereik van -1 tot 1, waarbij de cyclus elke 2 wordt herhaald Pi radialen of 360 graden, zoals blijkt uit de golfachtige grafiek die begint bij (0,1). In termen van calculus is de afgeleide van cos(x) − sin( X ), en zijn integraal levert sin( X )+ C , met C als integratieconstante. Deze functie strekt zich ook uit tot hyperbolische vormen, zoals cosh(x), waardoor de toepassing ervan in verschillende wiskundige contexten en oplossingen wordt verbeterd, inclusief golfberekeningen en oscillaties in fysieke systemen.
Cosinusfunctie: veelgestelde vragen
1. Wat is de cosinusfunctie?
De cosinusfunctie is een van de fundamentele trigonometrische functies. Het wordt in een rechthoekige driehoek gedefinieerd als de verhouding tussen de lengte van de zijde grenzend aan de betreffende hoek en de lengte van de hypotenusa.
2. Zijn Cos en Cosinus hetzelfde in trigonometrie?
Ja. cos is een afkorting/afkorting van de cosinusfunctie.
3. Wat is het bereik van de Cos-functie?
Het bereik van de cos- of cosinusfunctie bestaat uit alle reële getallen variërend van -1 tot 1, d.w.z. [-1,1].
4. Wat is het domein van de Cos-functie?
Het domein van de cos of de cosinusfunctie is de ser van alle reële getallen, dat wil zeggen: R .
5. Wat is de maximale waarde van de cosinusfunctie?
De maximale waarde van de cosinusfunctie is 1 voor alle hoeken gelijk aan 0° of 360°.
6. Wat is de minimumwaarde van de cosinusfunctie?
De minimumwaarde van de cosinusfunctie is -1 voor alle hoeken gelijk aan 180°.
7. Hoe vind ik de waarde van Cos(-x)?
De waarde van cos(-x) kan worden berekend door de waarde van cos(x) te berekenen vanwege het bestaan van de volgende identiteit: cos(-x) = cos(x).
8. Hoe de cosinusfunctie grafisch weergeven?
Om de grafiek van de cosinusfunctie op een cartesisch vlak te tekenen, verwijst u naar de x-as als representatie van hoeken in radialen (of graden) en de y-as als representatie van de waarden van de cosinusfunctie voor de corresponderende hoek op de x-as. Nu,
- Stap 1: Neem een subset van de x-as waarvoor u de grafiek wilt tekenen.
- Stap 2: Verdeel de x-as in dit bereik in punten op gelijke afstand (d.w.z. er is gelijke ruimte tussen alle subpunten). Merk op dat hoe groter het aantal delingen is, hoe groter de nauwkeurigheid van de resulterende grafiek.
- Stap 3: Markeer voor elk van deze subpunten x het punt (x, cos(x)) in de grafiek.
- Stap 4: Verbind alle gemarkeerde punten om de grafiek van de cosinusfunctie te verkrijgen (voor de subset van de x-as die u hebt geselecteerd).
9. Hoe vind ik de periode van een cosinusfunctie?
De periode van een cosinusfunctie verwijst naar het minimale bereik van waarden waarna de functie zichzelf begint te herhalen. We weten dat de cosinusfunctie zichzelf herhaalt na elke volledige rotatie, wat 2π radialen betekent. Daarom is de periode van de cosinusfunctie 2π radialen of 360°.
10. Wat is de amplitude van een cosinusfunctie?
De amplitude van een cosinusfunctie verwijst naar de maximale verplaatsing van de waarde van de functie vanaf de gemiddelde positie, dat wil zeggen de x-as. De amplitude van de cosinusfunctie is 1 aangezien de maximale verplaatsing 1 is (voor de waarden -1 en 1 bij respectievelijk 180 en 0 graden). Merk op dat het bereik van de cosinusfunctie [-amplitude, amplitude] is.
