A Functie in wiskunde is er een speciale relatie tussen de set invoerwaarden en de set uitvoerwaarden. In Functie geeft elke invoerwaarde een bepaalde uitvoerwaarde. We vertegenwoordigen een functie in de wiskunde als: y = f(x) waarbij X is de invoerwaarde en voor elk X we krijgen een uitvoerwaarde als y.

In dit artikel zullen we leren over, functies in de wiskunde, hun verschillende typen, voorbeelden en andere in detail.

Inhoudsopgave

• Wat is een functie in wiskunde?
• Functiedefinitie in wiskunde
• Functies Voorbeelden
• Voorwaarde voor een functie
• Vertegenwoordiging van functies in wiskunde
• Identificatie van functie
• Soorten functies
• Wat is een functie in algebra?
• Domein en bereik van een functie
• Samenstelling van functies
• Algebra van functies
• Wat is een functie in een grafiek?
• Grafische functies
• Gemeenschappelijke functies
• Toepassingen van functies
• Voorbeelden over Functie
• Oefen problemen met wat een functie is

Wat is een functie in wiskunde?

Een functie in de wiskunde is a relatie tussen de invoerwaarden (domein) en de uitvoerwaarden (bereik) van de gegeven sets, zodat geen twee variabelen uit de domeinsets aan dezelfde variabele in de bereikset zijn gekoppeld. Een eenvoudig voorbeeld van een functie in wiskunde is f(x) = 2x, die is gedefinieerd op R → R, hier is elke variabele in het domein gerelateerd aan slechts één variabele in het bereik.

Java-typeconversie en casting

Een functie in de wiskunde heeft een domein, codomein en bereik. Het domein is de verzameling van alle mogelijke waarden van x en het bereik van de functie is de verzameling van alle uitvoerwaarden van y. Het bereik is de subset van het codomein van een functie. We kunnen ook zeggen dat een functie in de wiskunde een relatie is met een unieke uitvoer en dat geen enkele invoerwaarde een vergelijkbare uitvoer heeft in een functie, wat het geval is voor een relatie.

Functiedefinitie in wiskunde

Functie is een speciale relatie of methode die elk lid van verzameling A verbindt met een uniek lid van verzameling B via een gedefinieerde relatie. Set A wordt het domein genoemd en set B het co-domein van de functie. Een functie in de wiskunde van set A naar set B wordt gedefinieerd als:

f = ∀ een ∈ A, b ∈ B

Elke functie is een relatie, maar elke relatie is geen functie. De criteria voor elke relatie die als een functie wordt beschouwd, aangezien elk element van set A in functie slechts één afbeelding in set B heeft, terwijl een element van set A in relatie meer dan één afbeelding in set B kan hebben.

We definiëren een functie in de wiskunde van niet-lege verzameling A naar niet-lege verzameling B, zodat:

(a, b) ∈ f, dan f(a) = b

waar we belden B als beeld van A gedefinieerd onder de relatie F .

Elk element 'A' van set A heeft een uniek beeld’ B ‘ in verzameling B dan is het een functie.

Functies Voorbeelden

Een functie in de wiskunde f wordt gedefinieerd als: y = f(x) waarbij X is de invoerwaarde, en voor elke invoerwaarde van x krijgen we een unieke waarde van y. Verschillende voorbeelden van de functies in wiskunde gedefinieerd op R → R zijn:

• y = f(x) = 3x + 4
• y = f(x) = zonde x + 3
• y = f(x) = -3x²+ 3, enz

Voorwaarde voor een functie

Voor elke twee niet-lege verzamelingen A en B, een functie f: A → B geeft dat aan F is een functie van A naar B, waarbij A is een domein en B is een co-domein.

Voor elk element, a ∈ A, een uniek element, b ∈ B, is er zo dat (a,b) ∈ f. Het unieke element b dat gerelateerd is aan a wordt aangegeven met f(a) en gelezen als f van a. Dit kan beter worden begrepen uit de onderstaande afbeelding:

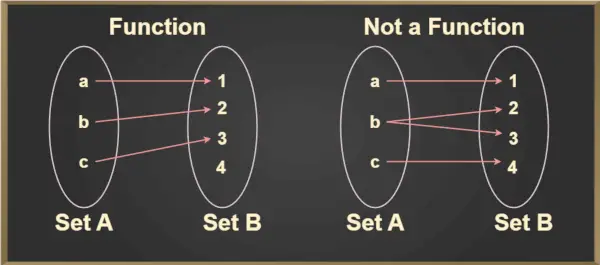
Verticale lijntest

Verticale lijntest wordt gebruikt om te bepalen of een curve een functie is of niet. Als een curve een verticale lijn op meer dan één punt doorsnijdt, is de curve geen functie.

Vertegenwoordiging van functies in wiskunde

We vertegenwoordigen een functie in de wiskunde als:

y = f(x) = x + 3

Hier is de reeks waarden van x het domein van de functie en de reeks uitvoerwaarden van y het co-domein van de functie. Hier wordt de functie gedefinieerd voor alle reële getallen omdat deze een unieke waarde geeft voor elke x, maar het is niet altijd mogelijk om de uitvoer voor elke waarde van x te krijgen. In dat geval definiëren we de functie in twee delen, dit kan worden opgevat als

• f(x) = 1/(x – 2), waarbij x ≠ 2
• f(x) = x²waarbij x ∈ {R}

We kunnen een functie in de wiskunde definiëren als een machine die enige invoer nodig heeft en een unieke uitvoer geeft. De functie f(x) = x²wordt hieronder gedefinieerd als,

We kunnen een functie in de wiskunde weergeven met de drie methoden als:

• Set bestelde paren
• Tabelformulier
• Grafische vorm

Als we bijvoorbeeld een functie weergeven als f(x) = x³

Een andere manier om dezelfde functie weer te geven is als de set bestelde paren als,

f = {(1,1), (2,8), (3,27)}

In de bovengenoemde verzameling is het domein van de functie D = {1, 2, 3} en het bereik van de functie R = {1, 8, 27}

Identificatie van functie

Functie wordt geclassificeerd als een speciaal type relatie in wiskunde. Er zijn de volgende regels die kunnen worden gebruikt om een ​​functie te identificeren:

• Een relatie waarin elke invoer die is toegewezen aan een unieke uitvoer een functie is. Dit heet één-op-één-functie.
• Een relatie waarin twee invoer (preimage) zijn toegewezen aan een enkele uitvoer is ook een functie. Dit is een veel-op-één-functie.
• Een relatie waarbij één ingang wordt afgebeeld op twee verschillende uitgangen is geen functie.
• Een relatie waarin veel inputs worden toegewezen aan veel outputs volgens geen specifieke regel, is geen functie.

Soorten functies

Verschillend Soorten functies worden gebruikt om verschillende soorten wiskundige problemen op te lossen, vooral gerelateerd aan curven en vergelijkingen. Er zijn drie hoofdtypen functies in de wiskunde die zijn gebaseerd op de elementtoewijzing van set A naar set B.

Injectieve functie of één-op-één-functie

De functie waarin elk element van het domein een aparte afbeelding heeft in het codomein, wordt de injectief of Eén-op-één-functie .

f: Er wordt gezegd dat A → B één-op-één of injectief is als de afbeeldingen van verschillende elementen van A onder f verschillend zijn, dat wil zeggen:

fa ₁ ) = b ₁ , f(een ₂ ) = b ₂

waar een₁, A₂∈A en b₁, B₂∈ B

Surjectieve functies of Onto-functie

Surjectieve functie is de functie waarin elk element van het codomein een voorafbeelding in het domein heeft. Het wordt ook wel genoemd Op functie wat betekent dat elk element van het codomein is gekoppeld aan elk element van het domein. Geen enkel element van codomain mag een lege relatie hebben. Het aantal elementen van codomain en bereik is hetzelfde.

f: Er wordt gezegd dat A → B op is, als elk element van B het beeld is van een element van A onder f, dat wil zeggen, voor elke b ϵ B bestaat er een element 'a' in A zodat f (a) = geb.

Bijectieve functie

Als een functie eigenschappen heeft van zowel Injective (One to One) als Surjective (Onto function), dan wordt de functie een Bijectieve functie . In Bijective Function is elk element van het domein gerelateerd aan elk element van het codomein en is er ook een één-op-één-relatie. Dit impliceert dat het aantal elementen van het codomein en het bereik hetzelfde zijn en dat geen enkel element in het domein of codomein een lege relatie heeft.

Op basis van de uitvoerwaarden worden de functies geclassificeerd als oneven en even functies. Laten we ze eens bekijken

Vreemde functies

Oneven functie is een type functie dat symmetrie vertoont rond de oorsprong. Concreet: als f(x) een oneven functie is, blijkt dat f(-x) = -f(x)

Gelijkmatige functie

Even-functie is een type functie dat symmetrie vertoont rond de y-as. Concreet: als f(x) een even functie is, blijkt dat f(-x) = f(x)

Wat is een functie in algebra?

Een functie binnen algebra is een vergelijking waarvoor elke x die in de vergelijking kan worden geplaatst, precies één uitvoer zal opleveren, zoals y uit de vergelijking. Het wordt weergegeven als y = f(x), waarbij x een onafhankelijke variabele is en y een afhankelijke variabele.

Bijvoorbeeld:

• y = 2x + 1
• y = 3x – 2
• y = 4j
• y = 5/x

Domein en bereik van een functie

Domein en bereik van een functie zijn respectievelijk de invoer- en uitvoerwaarde van een functie. Laten we bijvoorbeeld zeggen dat we een functie hebben die is gegeven als f(x) = x². Hier kunnen we het hele reële getal nemen als de invoerwaarde van x en de uitvoer zal altijd een positief reëel getal zijn. Daarom is het domein een verzameling van alle reële getallen weergegeven als R, terwijl het bereik een verzameling positieve reële getallen is, weergegeven als R⁺

Samenstelling van functies

Als f: A → B en g: B → C twee functies zijn. Vervolgens wordt de samenstelling van f en g aangegeven als f(g) en gedefinieerd als de functie mist = f(g(x)) voor x ∈ A.

Laten we twee functies nemen f(x) = x + 3 en g(x) = 2x²

mist = f(g(x))

⇒ mist = f(2x²)

⇒ tand = 2x²+ 3

Kom meer te weten, Samenstelling van functie

Algebra van functies

Algebra van functies omvat de algebraïsche bewerkingen die tussen twee functies worden uitgevoerd. De algebraïsche bewerking voor twee functies f(x) en g(x) gedefinieerd op basis van de reële waarde van x wordt hieronder vermeld:

• (f + g) (x) = f(x) + g(x)
• (f – g) (x) = f(x) – g(x)
• (f.g) (x) = f(x).g(x)
• (kf(x)) = k(f(x)); {Want k is een reëel getal}
• (f/g)(x) = f(x) /g(x); {Voor g(x) ≠ 0}

Wat is een functie in een grafiek?

Een functie kan eenvoudig in een grafiek worden weergegeven. Elke functie in de grafiek vertegenwoordigt een curve (inclusief een rechte lijn) in het x-y-vlak, in kaart gebracht voor de invoer- en bijbehorende uitvoerwaarden.

Om een ​​functie te plotten, moet je eerst een aantal punten vinden die op de functie liggen en deze punten vervolgens samenvoegen volgens de locus van de functie. Om bijvoorbeeld de functie (rechte lijn) f(x) = y = 5x – 2 te plotten, hebben we een punt in de grafiek nodig. Om het punt op de grafiek te vinden, nemen we eerst de willekeurige waarden van x en vinden dan de overeenkomstige waarden van y, als:

vind mijn iPhone vanaf Android

f(x) = y = 5x-2

als x = 0, y = 5(0) – 2 = -2 ⇒ (x, y) = (0, -2)

als x = 1, y = 5(1) – 2 = 3 ⇒ (x, y) = (1, 3)

als x = 2, y = 5(2) – 2 = 8 ⇒ (x, y) = (2, 8)

Nu we deze punten samenvoegen, kunnen we de grafiek krijgen van de functie y = 5x – 2

Grafische functies

Als u de waarden van x kent, kan een functie f(x) in een grafiek worden weergegeven. Omdat y = f(x), kunnen we de bijbehorende waarde voor y vinden door te beginnen met de waarden van x. Als gevolg hiervan kunnen we een grafiek in een coördinatenvlak plotten met behulp van x- en y-waarden. Overweeg het volgende scenario:

Stel dat y = x + 3

Wanneer x = 0, y = 3

Op dezelfde manier,

• x = -2, y = -2 + 3 = 1
• x = -1, y = -1 + 3 = 2
• x = 1, y = 1 + 3 = 4
• x = 2, y = 2 + 3 = 5
• x = 3, y = 3 + 3 = 6

Als gevolg hiervan kunnen we de grafiek voor functie x + 3 tekenen met behulp van deze waarden.

Gemeenschappelijke functies

Hieronder worden enkele algemene functies besproken die vaak in de wiskunde worden gebruikt:

Echte functie

Echte functie verwijst in wiskunde naar een functie waarvan het domein en het bereik deelverzamelingen zijn van de reële getallen (aangeduid als ℝ). In eenvoudiger bewoordingen is een reële functie een wiskundige regel of relatie die een reële getalswaarde toewijst aan elke reële getalinvoer.

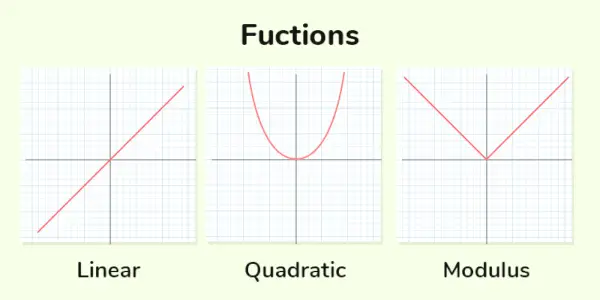
Echte functies

Polynomiale functie

De functie waarin de exponenten van algebraïsche variabelen niet-negatieve gehele getallen zijn, wordt a genoemd Polynomiale functie . Als de macht van de variabele 1 is, wordt het een lineaire functie genoemd, als de macht 2 is, wordt het een kwadratische functie genoemd, en als de macht 3 is, wordt het een kubieke functie genoemd. Enkele voorbeelden van polynoomfuncties worden hieronder vermeld:

• y = x²
• y = 2x + 3
• j = 3x³

Polynomiale functie kan verder worden ingedeeld in de volgende typen:

Lineaire functie : Lineaire functie is die waarbij het maximale vermogen van de variabele 1 is. De algemene vorm van Lineaire functie is y = mx + c

Kwadratische functie : Kwadratische functie is die waarbij het maximale vermogen van de variabele 2 is. Algemene vorm van kwadratische functie is, bijl ² + bx + c = 0

Kubieke functie : Kubieke functie is die waarbij het maximale vermogen van de variabele 3 is. Algemene vorm van de kubieke functie wordt gegeven als bijl ³ + bx ² + cx + d = 0

Omgekeerde functie

Omgekeerde functie is de functie die de inverse van een andere functie bevat. Laten we zeggen dat we een functie y = f(x) hebben, dan is de inverse functie ervan x = f^-1(y). In y = f(x) is het domein x en is het bereik y, terwijl in het geval van x = f^-1(y), het domein is y en het bereik is x. We kunnen dus zeggen dat het domein van de originele functie het bereik is van zijn inverse functie en dat het bereik van de originele functie het domein is van de originele functie. Enkele voorbeelden van inverse functies zijn:

willekeurig geen generator in Java

• y = dus^-1(X)
• y = x^-1

Gebiedsfunctie

Gebiedsfunctie verwijst doorgaans naar een wiskundige functie die het gebied van een geometrische vorm of gebied berekent. De oppervlaktefunctie neemt een of meer parameters als invoer en retourneert de oppervlakte van de overeenkomstige vorm. Hieronder worden enkele gebiedsfuncties besproken:

Gebied van cirkelfunctie : Gebied van cirkel (A) is een functie van zijn straal (r), zodat,

A = πr ²

Gebied van driehoeksfunctie : Gebied van Driehoek (A) is een functie van zijn basis (b) en hoogte (h), zodat:

A = (bh)/2

Exponentiële functie

Exponentiële functie is degene die wordt weergegeven als f(x) = e^X. Het wordt vaak gebruikt om snelle groei of verval te laten zien.

Logaritmische functie

Logaritmische functie is een wiskundige functie die de omgekeerde werking van machtsverheffing vertegenwoordigt. Het wordt weergegeven als f(x) = log x.

Plafondfunctie

Plafondfunctie , aangegeven als ⌈x⌉, rondt een reëel getal x naar boven af ​​op het dichtstbijzijnde gehele getal dat groter is dan of gelijk is aan x. Met andere woorden, het vindt de kleinste gehele waarde die groter is dan of gelijk is aan x.

Vloerfunctie

De vloerfunctie, aangegeven als ⌊x⌋, rondt een reëel getal x naar beneden af ​​op het dichtstbijzijnde gehele getal dat kleiner is dan of gelijk is aan x. Met andere woorden, het vindt de grootste gehele waarde die kleiner is dan of gelijk is aan x.

Modulus-functie

Modulus-functie , ook wel de absolute-waardefunctie genoemd, retourneert de grootte of grootte van een reëel getal, ongeacht het teken ervan. De modulusfunctie wordt aangegeven als ∣x∣, waarbij x de invoerwaarde is.

Signum-functie

Signum-functie , ook wel de tekenfunctie of signumfunctie genoemd, is een wiskundige functie die het teken van een reëel getal retourneert. Het geeft aan of het getal positief, negatief of nul is.

Trigonometrische functies

Trigonometrische functies zijn wiskundige functies die de hoeken van een rechthoekige driehoek in verband brengen met de lengtes van de zijden. De zes primaire goniometrische functies zijn sinus (sin), cosinus (cos), tangens (tan), cosecans (cosec), secans (sec) en cotangens (cot).

Complexe functies

Elke functie waarin de invoervariabele een complexe functie is, wordt de complexe functie genoemd. Een complex getal is een getal dat op het complexe vlak kan worden geplot. In een complex getal we hebben een reëel getal en een denkbeeldig getal. Een complex getal(z) wordt weergegeven als z= x + iy en een complexe functie wordt weergegeven als f(z) = P(x, y) + iQ(x, y)

Toepassingen van functies

Als we zeggen dat een variabele hoeveelheid y een functie is van een variabele hoeveelheid x, geven we aan dat y afhankelijk is van x en dat de waarde van y wordt bepaald door de waarde van x. Deze afhankelijkheid kan als volgt worden uitgedrukt: f = y (x).

• De straal van een cirkel kan worden gebruikt om de oppervlakte van een cirkel te berekenen. De straal r beïnvloedt gebied A. We verklaren dat A een functie is van r in de wiskundige taal van functies. We kunnen schrijven A = f(r) =π×r²
• Het volume V van een bol is een functie van zijn straal. V = f(r) = 4/3×r³geeft de afhankelijkheid van V van r aan.
• Kracht is een functie van de versnelling van een lichaam met een vaste massa m. F = g(a) = m×a.

Mensen lezen ook:

• Relatie en functie
  
• Domein en bereik van goniometrische functies
• Bereik van een functie
• Hyperbolische functie

Voorbeelden over Functie

Voorbeeld 1: Voor twee functies worden f en g gedefinieerd als f(x) = x ² en g(x) = ln(2x). Zoek de samengestelde functie (gof )( x )

Oplossing:

Gegeven:

• f(x) = x²
• g(x) = ln(2x)

(gof)( X ) = g (f (x))

[g (f (x)] = ln(2f(x))

= ln(2x²)

= 2 ln(√2x)

Dus (gof)(x) = 2 ln(√2x)

Voorbeeld 2: Vind de uitvoer van de functie g(t)= 6t ² + 5 bij

• (ik) t = 0
• (ii) t = 2

Oplossing:

Gegeven functie,

g(t)= 6t²+ 5t

• (ik) t = 0

g(0) = 6(0)²+5(0) = 0 + 0

g(0) = 0

• (ii) t = 2

g(2) = 6(2)²+5(2)

g(2) = 24 + 10

g(2) = 34

Voorbeeld 3: De lengte van een rechthoek is vijf keer de breedte. Druk de oppervlakte van de rechthoek uit als functie van de lengte.

Oplossing:

Stel dat de lengte van de rechthoek l is en de breedte van de rechthoek b

Nu,

• b = l/5

Oppervlakte van rechthoek(A) = l × l/5 = l²/5

Dus de oppervlakte van de rechthoek als functie van de lengte is:

EEN(l) = l ² /5

Oefen problemen met wat een functie is

1. Gegeven de functie f(x)=3x+5

• Vind f(2)
• Vind f(−1)
• Bepaal het domein en het bereik van de functie.

2. Gegeven de functie g(x)=x ² – 4x + 3

• Zoek de wortels van de functie.
• Zoek g(3) en g(0).
• Bepaal het hoekpunt van de functie.

3. Gegeven twee functies f(x)=x + 2 en h(x)=2x – 3

• Zoek de samengestelde functie (f ∘ h) (x)
• Evalueer (f ∘ h)(2)

Samenvatting – Wat is een functie

Een functie in de wiskunde is een speciale relatie tussen invoerwaarden (domein) en uitvoerwaarden (bereik), waarbij elke invoer wordt geassocieerd met een unieke uitvoer. Functies, weergegeven als y = f(x), hebben specifieke kenmerken en kunnen worden gevisualiseerd met behulp van geordende paren, tabellen of grafieken. Ze zijn essentieel bij verschillende wiskundige problemen en zijn er in verschillende typen, waaronder injectief (één-op-één), surjectief (op) en bijectief (beide). Functies kunnen worden getest met behulp van de verticale lijntest en worden verder geclassificeerd in polynomiale, inverse, exponentiële, logaritmische en trigonometrische functies. Het begrijpen van functies omvat het herkennen van hun domein, bereik en de regels die deze definiëren. Voorbeelden hiervan zijn eenvoudige lineaire functies zoals y = 2x + 1 en complexe samenstellingen van functies. Functies spelen een cruciale rol in de algebra, meetkunde en calculus, en helpen bij de representatie en analyse van wiskundige relaties en verschijnselen uit de echte wereld.

Veelgestelde vragen over wat een functie is

Wat is de definitie van een functie?

Een relatie f gedefinieerd op een set A met een andere set B wordt in de wiskunde een functie genoemd als elke waarde van A een unieke waarde heeft in set B.

Hoe schrijf je een functie in wiskunde?

De functie f in de wiskunde wordt weergegeven als f: A → B en wordt gedefinieerd als: f(x) = x+2. Hier hebben we voor elke unieke waarde van x een unieke waarde van y.

Hoe transformeer je een functie?

We kunnen een functie gemakkelijk naar andere functies transformeren door eenvoudigweg algebraïsche basisbewerkingen op de functie uit te voeren. De verschillende transformaties van de functie zijn reflectie, translatie, rotatie, enz.

Wat is een rationele functie?

Een breukfunctie waarbij de teller en de noemer polynomiale functies zijn, wordt de rationale functie genoemd. Enkele voorbeelden van de rationele functie zijn:

Java-lijst maken

• f(x) = x ² /(2x + 3)
• g(x) = (6x + 3)/(x – 1), enz.

Wat is een lineaire functie?

Een algebraïsche functie waarin elke term van de functie constant is of een macht van één heeft, wordt een lineaire functie genoemd. Enkele voorbeelden van de lineaire functie zijn:

• f(x) = 2x + 3
• g(x) = x – 5, enz.

Wat zijn domein en codomein van een functie?

Als we de functie definiëren als: y = f(x). Het domein van de x bestaat dan uit alle waarden van x waarvoor y resulteert in een unieke waarde. En het co-domein van y is de verzameling van alle waarden van y voor elke waarde van x.

Hoe herken je een functie in de wiskunde?

Als een invoerwaarde(x) van het domein in een relatie meer dan één afbeelding (y) heeft, kan deze relatie nooit een functie zijn. Dus als de waarde van x wordt herhaald in het geordende paar, is het nooit een functie.