De hoek wordt gemeten in graden (°) en radialen. Het wordt gevormd tussen de twee aangrenzende zijden van een veelhoek. Elke veelhoek heeft verschillende zijden en een verschillend aantal hoeken. De formule om de hoeken in graden te vinden is handig in de meetkunde en trigonometrie. Het is essentieel om andere concepten van de wiskunde te begrijpen, zoals boog, een centrale hoek van de cirkel, enz.
- Een volledige cirkel = 360°
- Een rechte lijn = 180°
- Een halve cirkel= 180°
- Een kwart cirkel = 90°
Hoeken in graden berekenen
Er zijn drie verschillende methoden om hoeken in graden te vinden, namelijk:
- Gebruik van de beschermer D
- Gebruik van de stelling van Pythagoras en de trigonometriefunctie in een rechthoekige driehoek
- Gebruik de formule voor de som van de hoeken
- Centrale hoek van een cirkel
Gebruik van de beschermer D
Een beschermer is een soort liniaal of schaal die wordt gebruikt om de afstand in centimeters of millimeters te meten. De beschermer die wordt gebruikt om hoeken te meten heeft de vorm ‘D’, waarbij de waarde van de hoeken is gemarkeerd van 0 tot 180 ° vanuit beide richtingen (rechts of links). We moeten de as uitlijnen met de lijn op de D om de hoek te meten. De middelste cirkel van de beschermer is uitgelijnd met het hoekpunt van de te meten hoek. De stralen langs het hoekpunt helpen je de hoek in graden te vinden.
Gebruik van de stelling van Pythagoras en de trigonometriefunctie in een rechthoekige driehoek
In trigonometrie zijn er zes functies, sinus, cos, cosec, bruinen, kinderbed, En sec. Een rechthoekige driehoek heeft drie zijden: basis, loodrecht en hypotenusa.
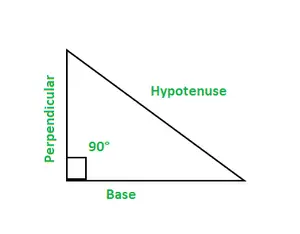
- Basis: Het is een zijde die grenst aan de hoek van 90°. Loodrecht: Het is ook een zijde die grenst aan de hoek van 90°. Hypotenusa: Het is een zijde die tegenovergesteld is aan de hoek van 90°.
Een rechthoekige driehoek wordt weergegeven door een hoek van 90° als een van de hoeken. De totale som van de hoek van een driehoek is 180°.
- Cosecθ: Het wordt weergegeven als hypotenusa gedeeld door loodrecht.
Cosecθ =
- Cotθ: Het wordt weergegeven als basis gedeeld door de loodlijn.
Cotθ =
De andere trigonometrische functies worden weergegeven als:
zondeθ =
Cosθ =
tanθ =
secθ =
Cosecθ kan ook worden weergegeven als 1/sinθ
secθ kan ook worden weergegeven als 1/cosθ
Cotθ kan ook worden weergegeven als 1/tanθ
Waar,
Java 8-functiesΘ is de hoek
De stelling van Pythagoras
Als er twee zijden van een rechte hoek bekend zijn, kunnen we eenvoudig de derde zijde van een rechthoekige driehoek berekenen. In een rechthoekige driehoek wordt de stelling van Pythagoras gegeven door:
(Hypotenusa)2= (basis)2+ (loodrecht)2
Formule voor de som van de hoeken
De som van de hoeken verwijst naar de totale som van de interne hoeken van een veelhoek die zich tussen de twee zijden vormt. Als er zes zijden van een veelhoek zijn, zijn er ongeveer zes hoeken. Het helpt om een hoek te vinden als andere hoeken en de som van de hoeken van een veelhoek bekend zijn.
De formule om de totale som van de hoeken van een veelhoek te vinden wordt gegeven door:
Totale som van hoeken = 180 (n – 2)
Waar,
n is het aantal zijden van een veelhoek
Voorbeeld:
- Als n = 4,

Totale som van hoeken = 180 (4 – 2)
= 180 (2)
= 360°
Als n = 5,
Totale som van hoeken = 180 (5 – 2)
= 180 (3)
= 540°
- Als n = 6

Totale som van hoeken = 180 (6 – 2)
= 180 (4)
= 720°
Centrale hoek van een cirkel
Een cirkel is een figuur met een ronde vorm waarvan de grens op gelijke afstand ligt van het middelpunt. De afstand tussen het middelpunt en de grens staat bekend als de straal van de cirkel. De hoek gevormd door de twee stralen van de cirkel staat bekend als de centrale hoek. De waarde van de centrale hoek van een cirkel ligt tussen 0 en 360 graden.

De formule om de middelpuntshoek van een cirkel te berekenen wordt gegeven door:
Booglengte = 2πr × (θ/360)
Θ = 360L/2pr
Waar,
r is de straal van de cirkel
AB is de boog
Theta is de hoek in graden.
L = Booglengte
Voorbeeldproblemen
Vraag 1: Vind de centrale hoek van een cirkel met een straal van 2 m en een booglengte van 4 m?
Oplossing :
De formule om de middelpuntshoek van een cirkel te berekenen wordt gegeven door:
Θ = 360L/2pr
Waar,
r is de straal van de cirkel
Theta is de hoek in graden.
L = Booglengte
Θ = Hoek in graden
r=2m
L=4m
Θ = 360 × 4 /2 × π × 2
Θ = 114,6°
De centrale hoek van de cirkel is dus 114,6°.
Vraag 2: Vind de centrale hoek van een cirkel met een straal van 10 cm en een booglengte van 18 cm?
vind geblokkeerde nummers op Android
Oplossing :
De formule om de middelpuntshoek van een cirkel te berekenen wordt gegeven door:
Θ = 360L/2pr
Waar,
r is de straal van de cirkel
Theta is de hoek in graden.
L = Booglengte
r = 10 cm
L = 18 cm
Θ = Hoek in graden
Θ = 360 × 18/2 × π × 10
Θ = 103,13°
De centrale hoek van de cirkel is dus 103,13°.
Vraag 3: Vind de hoek van een parallellogram als de andere drie hoeken 80°, 95° en 105° zijn?
Oplossing :
Er zijn vier zijden in een parallellogram met de totale som van de hoeken 360°.
Formule om de som van de hoeken = 180 (n – 2) te vinden
Waar,
n is het aantal zijden van een veelhoek
Hier, n = 4,
De totale som van de hoeken = 180 (4 – 2)
= 180 (2)
= 360°
Totale som = Hoek 1 + Hoek 2 + Hoek 3 + Hoek 4
360 = 80+ 95+ 105+ Hoek 4
360 = 280 + Hoek 4
Hoek 4 = 360 – 280
Hoek 4 = 80°
Vraag 4: Zoek hoek A in de gegeven figuur.

Oplossing :
Gegeven: Hypotenusa = 12
Loodrecht = 6
De trigonometriefunctie om de hoek te berekenen wordt gegeven door:
sinA = 6/12
A = 30°
Vraag 5: Zoek hoek A in de gegeven figuur.

Oplossing :
Gegeven: Hypotenusa = 10
Basis= 5
De trigonometriefunctie om de hoek te berekenen wordt gegeven door:
CosA = 5/10
zonnige deol-leeftijdA = 60°
Vraag 6: Vind de hoek van een vijfhoek als de andere vier hoeken 115°, 100°, 105° en 100° zijn?
Oplossing :
Er zijn vijf zijden in een vijfhoek met de totale som van de hoeken 540°.
Formule om de som van de hoeken = 180 (n – 2) te vinden
Waar,
n is het aantal zijden van een veelhoek
Hier, n = 5,
Totale som van hoeken = 180 (5 – 2)
= 180 (3)
= 540°
Totale som = Hoek 1 + Hoek 2 + Hoek 3 + Hoek 4 + Hoek 5
540 = 115° + 100° + 105°+100° + Hoek 5
540 = 420 + Hoek 5
Hoek 5 = 540 – 420
Hoek 5 = 120°
Vraag 7: Zoek hoek A in de gegeven figuur.

Oplossing :
Gegeven: Basis = √3
Loodrecht = 1
De trigonometriefunctie om de hoek te berekenen wordt gegeven door:
tanθ =
tanθ = 1/√3
A = 30°
Vraag 8: Vind de hoek van een parallellogram als de andere drie hoeken 100°, 70° en 80° zijn?
Oplossing :
Er zijn vier zijden in een parallellogram met de totale som van de hoeken 360°.
Formule om de som van de hoeken = 180 (n – 2) te vinden
Waar,
n is het aantal zijden van een veelhoek
Hier, n = 4,
Totale som van hoeken = 180 (4 – 2)
poep= 180 (2)
= 360°
Totale som = Hoek 1 + Hoek 2 + Hoek 3 + Hoek 4
360 = 100 + 70 + 80 + Hoek 4
360 = 250 + Hoek 4
Hoek 4 = 360 – 250
Hoek 4 = 110°
De andere hoek is dus 110°.
Vraag 9: Vind de hoek van een zeshoek als de andere vijf hoeken 120°, 115°, 110°, 125° en 105° zijn?
Oplossing :
Er zijn zes zijden in een zeshoek met de totale som van de hoeken 720°.
Formule om de som van de hoeken te vinden = 180 (6 – 2)
Waar,
n is het aantal zijden van een veelhoek
Hier, n = 6,
Totale som van hoeken = 180 (6 – 2)
= 180 (4)
= 720°
Totale som = Hoek 1 + Hoek 2 + Hoek 3 + Hoek 4 + Hoek 5 + Hoek 6
720 = 120 + 115 + 110 + 125 + 105 + Hoek 6
720 = 575 + Hoek 6
Hoek 6 = 720 – 575
Hoek 6 = 145°
De zesde hoek van de zeshoek is dus 145°.






