OPPERVLAKTEFORMULES - TABEL MET OPPERVLAKTEFORMULES VOOR VERSCHILLENDE VORMEN

Gebiedsformules voor verschillende objecten zijn de formules die worden gebruikt om de oppervlakte van verschillende objecten te vinden. Oppervlakte is de ruimte die wordt ingenomen door de grens van een figuur. Oppervlakteformules van verschillende geometrische vormen zijn afhankelijk van verschillende parameters, zoals afmetingen, hoogte en straal van verschillende geometrische vormen. Er zijn twee soorten geometrische vormen:

Tweedimensionale vormen (2D-vormen)
Driedimensionale vormen (3D-vormen)

In dit artikel zullen we gebiedsformules leren voor verschillende 2D- en 3D-vormen, zoals de oppervlakte van een rechthoek, de oppervlakte van een vierkant, de oppervlakte van een cirkel, de oppervlakte van een kubus, enz. en andere in detail.

Inhoudsopgave

Wat is gebied?
Wat zijn gebiedsformules?
Wat zijn 2D-vormen?
Gebied van formule voor 2D-vormen
Tabel met gebiedsformules
Wat zijn 3D-vormen?
Gebied van formule voor 3D-vormen
Voorbeelden van gebiedsformules

Wat is gebied?

De ruimte die wordt ingenomen door de grens van een figuur wordt de oppervlakte van de figuur genoemd. Het wordt gemeten in vierkante eenheden. De SI-eenheid om de oppervlakte te meten is m². Oppervlakte wordt gebruikt in verschillende wiskundige concepten en wordt ook gebruikt in scenario's uit het echte leven, zoals het vinden van de oppervlakte van een kamer, een oppervlaktetabel, enz. en andere.

Wat zijn gebiedsformules?

Oppervlakteformules zijn essentiële hulpmiddelen die in de wiskunde worden gebruikt om de hoeveelheid ruimte te berekenen die wordt ingesloten door verschillende tweedimensionale vormen. Deze formules kunnen worden gebruikt om het geometrische gebied te vinden figuren zoals vierkanten, rechthoeken, cirkels, driehoeken, trapeziums en ellipsen. Door deze formules te gebruiken, kunnen we de oppervlakte van verschillende vormen nauwkeurig berekenen, waardoor we problemen uit de echte wereld kunnen oplossen en belangrijke berekeningen kunnen maken.

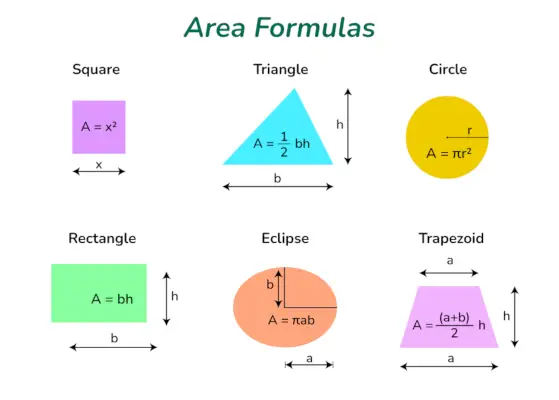
Gebiedsformules

Wat zijn 2D-vormen?

Vormen die slechts twee dimensies hebben, worden de 2D-vormen . Ze worden in de 2D-ruimte getekend en zijn afhankelijk van 2 parameters, doorgaans lengte(l) en breedte(b). De verschillende 2D-vormen zijn, Rechthoek, Vierkant, Driehoek, Cirkels en andere.

Gebied van formule voor 2D-vormen

Formules voor oppervlakte van 2D-vormen is de formule die wordt gebruikt om de oppervlakte van de verschillende 2D-vormen te berekenen, zoals de oppervlakte van een driehoek, de oppervlakte van een vierkant, de oppervlakte van de rechthoek, de oppervlakte van de ruit, enz. Deze oppervlakteformules worden veel gebruikt in de wiskunde om verschillende geometrische problemen oplossen. Verschillende gebiedsformules voor verschillende vormen zijn,

Oppervlakteformule van een rechthoek

Rechthoek is een tweedimensionaal figuur dat is een vierhoek, d.w.z. het heeft vier zijden, de tegenoverliggende zijden zijn evenwijdig en gelijk. Alle hoeken in de rechthoek zijn gelijk en hun maat is 90 graden. De diagonalen van de rechthoek zijn gelijk en zijn loodrechte middelloodlijnen van elkaar.

De formule voor het berekenen van de oppervlakte van een rechthoek is met lengte en l en breedte B is,

Oppervlakte van rechthoek (A) = l×b vierkante eenheden

Oppervlakteformule van een vierkant

Vierkant is een tweedimensionale figuur die een vierhoek is, dat wil zeggen dat hij vier zijden heeft, de tegenoverliggende zijden zijn evenwijdig en alle vier zijden in een vierkant zijn gelijk. Alle hoeken in het vierkant zijn gelijk en hun maat is 90 graden. De diagonalen van het vierkant zijn gelijk en zijn loodrechte middelloodlijnen van elkaar.

De formule voor het berekenen van de oppervlakte van een vierkant met zijde A is,

Oppervlakte van vierkant (A) = a ² vierkante eenheden

Oppervlakteformule van een driehoek

Driehoek is de eenvoudigste veelhoek die wordt gemaakt door drie rechte lijnen met elkaar te verbinden. Zoals de naam al doet vermoeden is het een veelhoek met drie hoeken. De som van de lengtes van alle zijden van de driehoek is de omtrek van de driehoek en de ruimte binnen de omtrek van de driehoek is de oppervlakte van de driehoek.

niet nul in js

De formule voor het berekenen van de oppervlakte van een driehoek met basis B is en hoogte H is,

Oppervlakte van driehoek (A) = 1/2 × bh vierkante eenheden

Oppervlakteformule van een cirkel

Cirkel is een geometrische figuur zonder rechte lijn. Het is de plaats van het punt dat zich altijd op een constante afstand van het vaste punt bevindt. Het vaste punt wordt het middelpunt van de cirkel genoemd en de vaste afstand is de straal van de cirkel.

De formule voor het berekenen van de oppervlakte van een cirkel met r als de straal van de cirkel is,

Oppervlakte van cirkel (A) = πr ² vierkante eenheden

Oppervlakteformule van een parallellogram

Parallellogram is een 2D-figuur waarbij de tegenoverliggende zijden evenwijdig en gelijk zijn. De formule voor het berekenen van de oppervlakte van het parallellogram met basis B en hoogte H Zijn,

Gebied van parallellogram (A) = bh vierkante eenheden

Oppervlakteformule van een ruit

Ruit is een vierhoek met alle vier de zijden gelijk en evenwijdig, maar niet alle hoeken zijn gelijk. De formule voor het berekenen van de oppervlakte van de ruit met diagonaal D ₁ En D ₂ Zijn,

Oppervlakte van Ruit (A) = 1/2 × d ₁ × d ₂ vierkante eenheden

Oppervlakteformule van een trapezium

Trapezium is een andere naam trapezium . Het is een vierhoek waarvan de tegenoverliggende zijden evenwijdig zijn. De formule voor het berekenen van de oppervlakte van een trapezium met evenwijdige zijden A En B en hoogte H is,

Oppervlakte van trapezium (A) = 1/2(a +b)h vierkante eenheden

Oppervlakteformule van een ellips

Ellips is een 2D-vorm en valt onder kegelvormige secties. De formule voor het berekenen van de oppervlakte van een ellips met as as A En B Zijn,

Oppervlakte van ellips (A) = πab vierkante eenheden

Oppervlakteformule van een halve cirkel

Halve cirkel is een 2D-figuur die de helft van een cirkel is. De formule om de oppervlakte van een halve cirkel met straal r te berekenen is:

Oppervlakte van halve cirkel (A) = 1/4(πr ² ) vierkante eenheden

Tabel met gebiedsformules

De formules voor de oppervlakten van de verschillende 2D-figuren zijn toegevoegd in de onderstaande tabel,

Figuren	Formule	Variabelen
Rechthoek	Oppervlakte = l×b	Ik is de lengte b is de breedte
Vierkant	Oppervlakte = een²	a is de zijde van het vierkant
Driehoek	Oppervlakte = 1/2×bh	b is de basis h is de hoogte
Cirkel	Oppervlakte = πr²	r is de straal van de cirkel
Trapezium	Oppervlakte = 1/2×(a+b)h	a is het eerste honk b is het tweede honk
Ruit	Oppervlakte = 1/2×d₁×d₂	D₁is de Ene Diagonaal D₂is de tweede diagonaal
Parallellogram	Oppervlakte = b × h	b is de basis h is de hoogte
Ovaal	Oppervlakte = πab	a is de straal van de hoofdas b is de straal van de kleine as

Wat zijn 3D-vormen?

3D-vormen zijn de vormen die in 3D-ruimtes worden getekend. Ze hebben 3 dimensies die hun parameters zijn. De oppervlakte van deze vormen is afhankelijk van de lengte, breedte en hoogte van 3D-vormen. Verschillende 3D-vormen zijn: kubus, kubusvormig, cilinder, kegel, bol en andere. Het gebied van 3D-vormen bestaat uit twee categorieën: Gebogen oppervlak (lateraal oppervlak){CSA} en Totaal oppervlak (TSA). De CSA is de oppervlakte van het gehele gebogen oppervlak van de 3D-vormen en de TSA is de oppervlakte van alle vlakken van de 3D-vormen.

Gebied van formule voor 3D-vormen

Het gebied van de 3D-vormen is de ruimte die wordt ingenomen door alle gezichten van de figuur. Het wordt gemeten in eenheid². De SI-oppervlakte-eenheid is m². De oppervlakte van de kubus , gebied van kubusvormig , gebied van cilinder, gebied van kegel en andere komen op het gebied van 3D-vormen. De onderstaande tabel toont de formules van verschillende 3D-figuren.

Gebied van vorm	Oppervlakte	Parameters
Gebied van kubus	6a²	a is de lengte van de rand
Gebied van kubusvormig	2(lb + lh + bh)	l is de lengte van de rand b is de breedte van de rand h is de hoogte van de rand
Gebied van kegel	πr(r + l)	r = straal van cirkelvormige basis l = schuine hoogte
Gebied van cilinder	2π(r+h)	r = straal van cirkelvormige basis h = hoogte van de cilinder
Gebied van bol array in Java-methoden	4πr²	r is de straal van de bol
Gebied van het halfrond	3πr²	r is de straal van het halfrond
Gebied van rechthoekig prisma	2(wl + hl + hw)	l is de lengte van de rand w is de breedte van de rand h is de hoogte van de rand

Controleer ook

Formules voor oppervlakte en omtrek

Formules voor oppervlakte

Voorbeelden van gebiedsformules

Voorbeeld 1: Zoek de oppervlakte van een rechthoek met een lengte van 5 cm en een breedte van 2 cm.

Oplossing:

Gegeven,

Lengte van de rechthoek (l) = 5 cm

Breedte van de rechthoek (b) = 2 cm

Oppervlakte van rechthoek (A) = l × b

A = 5 cm × 2 cm
= 10cm²
teken naar int in Java

Voorbeeld 2: Zoek de oppervlakte van het vierkante park waarvan de zijde 4 m is.

Oplossing:

Gegeven,

Zijde van vierkant (a) = 4 m

Oppervlakte van vierkant = a²
= (4)²= 16 meter²

De oppervlakte van het vierkante park is dus 16 m2²

Voorbeeld 3: Zoek de oppervlakte van een driehoekige plaat waarvan de hoogte 6 cm is en de basis 6 cm.

Oplossing:

Gegeven,

Hoogte driehoek (h) = 6 cm

Basis van driehoek (b) = 8 cm

Oppervlakte van driehoek(A) = 1/2(b × h)

EEN = 1/2(8 × 6)
= 48/2 = 24cm²

De oppervlakte van de driehoekige plaat is 24 cm²

Voorbeeld 4: Zoek de oppervlakte van een ronde schijf met een straal van 1,4 cm.

Oplossing:

Gegeven,

Straal van cirkel (r) = 1,4 cm

Oppervlakte van cirkel(A) = πr²

EEN = π(1,4)²
= 22/7(1,4)(1,4) = (4,4)(1,4)
= 6,16 cm²

De oppervlakte van de ronde schijf is 6,16 cm²

Veelgestelde vragen over gebiedsformules

Wat zijn gebiedsformules?

De oppervlakteformules zijn de formules die worden gebruikt om de oppervlakte van een figuur te vinden. Het wordt gebruikt om de hoeveelheid ruimte te vinden die door de figuur wordt ingenomen. Over het algemeen wordt het gebied weergegeven met de letter ‘A’. en wordt gemeten in eenheid², d.w.z. cm², M², enz.

Wat is de oppervlakteformule voor vierkant?

De oppervlakteformule voor een vierkant is de formule om de ruimte te berekenen die door het vierkant wordt ingenomen. De formule om de oppervlakte van het vierkant te berekenen is:

Oppervlakte van vierkant = (zijde) ²

Wat is de oppervlakteformule voor rechthoek?

De oppervlakteformule voor een rechthoek is de formule om de ruimte te berekenen die door de rechthoek wordt ingenomen. De formule om de oppervlakte van de rechthoek te berekenen is:

Gebied van rechthoek = lengte x breedte

Wat is de oppervlakteformule voor driehoek?

De oppervlakteformule voor een driehoek is de formule om de ruimte te berekenen die door de driehoek wordt ingenomen. De formule om de oppervlakte van de driehoek te berekenen is:

Oppervlakte van driehoek = 1/2 (basis × hoogte)

Wat is de oppervlakteformule voor cirkel?

De oppervlakteformule voor een cirkel is de formule om de ruimte te berekenen die door de cirkel wordt ingenomen. De formule om de oppervlakte van de cirkel te berekenen is:

Oppervlakte van cirkel = π(straal) ²

Wat is de oppervlakteformule voor vierhoek?

Formule om de oppervlakte van een vierhoek te berekenen,

Oppervlakte van vierhoek = 1/2 × diagonaal ₁ × Diagonaal ₂

Wat is de oppervlakteformule van een driehoekig prisma?

De formule voor het gebied van een driehoekig prisma is:

Oppervlakte van driehoekig prisma = (omtrek van basis x lengte van prisma) + 2 x basisoppervlak

Wat is de oppervlakteformule van veelhoek?

De formule om de oppervlakte van een veelhoek te berekenen is:

Oppervlakte van veelhoek = 1/2 × (omtrek × Apothema)

Wat is de oppervlakteformule van een rechthoekige driehoek?

De formule voor de oppervlakte van een rechthoekige driehoek is:

Oppervlakte van de rechter driehoek = 1/2 × loodrecht × basis

Wat is de oppervlakteformule van het Pentagon?

De formule voor de oppervlakte van het Pentagon is:

Oppervlakte van Pentagon = 1/2 × Omtrek × Apothem