Trapezium in wiskunde: Een trapezium is een veelhoek met vier zijden, d.w.z. het is een vierhoek. Trapezium is afgeleid van het Griekse woord trapeze, wat tafel betekent. Het is een complexe vierhoek. Een trapezium is een bijzondere vierhoek met slechts één paar evenwijdige zijden. Een trapezium is een tweedimensionale vorm die eruitziet als een tafel.
Een trapezium heeft vier zijden en vier hoekpunten. We zien de trapeziumvorm in ons dagelijks leven en het is een van de meest voorkomende vormen. In dit artikel zullen we meer te weten komen wat is trapezium in wiskunde, de eigenschappen, formules, voorbeelden en soorten trapezium, samen met enkele opgeloste voorbeelden ervan.
Inhoudsopgave
- Wat is een trapezium in wiskunde?
- Soorten trapezium
- Onregelmatig trapezium
- Eigenschappen van trapezium
- Trapezium-formule
- Gebied van trapeziumformule
- Omtrek van trapeziumformule
- Verschil tussen trapezium en trapezium
- Hoeken van trapezium
- Diagonaal van Trapezium
- Trapeziumvoorbeelden
Wat is een trapezium in wiskunde?
Een trapezium is een gesloten tweedimensionale vierhoek met een paar parallelle tegenoverliggende zijden. De parallelle zijden van een trapezium worden bases genoemd en de niet-parallelle zijden van een trapezium worden poten genoemd. Het trapezium heeft vier zijden en vier hoeken. A parallellogram wordt ook wel een trapezium met twee evenwijdige zijden genoemd.
Trapezium-definitie
Een trapezium is een vierhoek (een vierhoek) met minstens één paar evenwijdige zijden. Deze parallelle zijden worden de basis van het trapezium genoemd, en de andere twee zijden worden de benen genoemd, die niet noodzakelijk evenwijdig zijn.
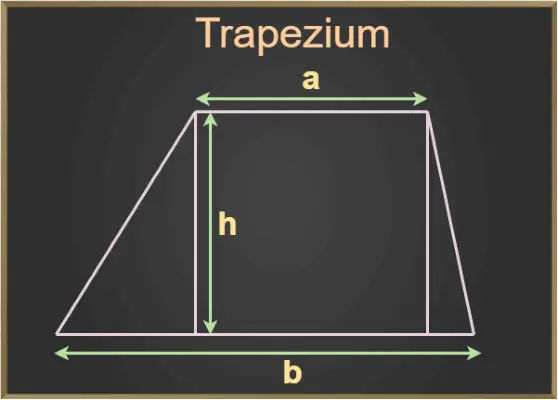
In de bovenstaande figuur zijn a en b de basis van het trapezium en h de hoogte van het trapezium.
Trapeziumvorm
Trapezium is een vierhoek dat wil zeggen een veelhoek met vier zijden. Een trapezium heeft vier zijden met een paar tegenoverliggende zijden evenwijdig aan elkaar. De trapeziumvorm komt veel voor en we zien in ons dagelijks leven verschillende dingen die lijken op het trapezium. Enkele door ons waargenomen voorbeelden van trapezium uit de praktijk zijn trapeziumvormige tafels, tegels, schilderijen en andere.
Soorten trapezium
Op basis van de zijkanten en de hoeken bestaat het trapezium uit drie typen:
- Scalene Trapezium
- Gelijkbenig trapezium
- Rechter trapezium

Gelijkbenig trapezium
Het trapezium met gelijke lengte poten wordt een gelijkbenig trapezium genoemd, dat wil zeggen dat in een gelijkbenig trapezium de twee niet-parallelle zijden gelijk zijn.
Scalene Trapezium
Een trapezium waarvan alle zijden niet gelijk zijn, wordt een scalenetrapezium genoemd. In een scalenetrapezium zijn geen twee hoeken gelijk.
Rechter trapezium
Een trapezium met een paar rechte hoeken, grenzend aan elkaar, staat bekend als een rechts trapezium.
Onregelmatig trapezium
Een trapezium heeft één paar evenwijdige zijden en de andere twee zijden zijn niet evenwijdig. Bij een regulier trapezium zijn de andere twee niet-parallelle zijden gelijk, maar bij een onregelmatig trapezium zijn de twee niet-parallelle tegenoverliggende zijden ongelijk.
Eigenschappen van trapezium
Er zijn verschillende eigenschappen van trapezium, waarvan sommige als volgt zijn:
- Parallelle zijden: Een trapezium heeft twee parallelle zijden, die bases worden genoemd. Voorbeeld: Zijden AB en CD zijn evenwijdig aan elkaar, weergegeven in de figuur.
- Niet-parallelle zijden: Niet-parallelle zijden van een trapezium worden de poten genoemd en de poten van een trapezium zijn niet even lang. Voorbeeld: Zijden AD en BC zijn niet-parallelle zijden van het trapezium.
- Hoogte of hoogte: De loodrechte afstand tussen de bases wordt de hoogte of hoogte van het trapezium genoemd. In het bovenstaande diagram is h de hoogte van het trapezium.
- Som van hoeken
- Aangrenzende binnenhoeken in trapeziumvorm tot 180°. Voorbeeld: Er zijn twee paar co-binnenhoeken. Eén paar is ∠ A en ∠ D, terwijl het andere paar ∠ B en ∠ C is. De som van elk paar co-binnenhoeken is 180°.
- De som van alle binnenhoeken in een trapezium is altijd 360°. Voorbeeld : In de figuur is ∠A+∠D 180° en ∠B+∠C 180°. Daarom is ∠A+∠D +∠B+∠C = 360°.
- Mediaan: De mediaan van een trapezium is het lijnsegment dat de middelpunten van de benen verbindt. De mediaan is evenwijdig aan de bases en de lengte is het gemiddelde van de lengtes van de bases.
- Trapezium heeft precies één paar tegenoverliggende zijden die evenwijdig zijn.
Trapezium-formule
Belangrijke formules van een Trapezium zijn:
- Gebied van Trapezium = ½ (Som van parallelle zijden) × (afstand tussen parallelle zijden)
- Omtrek van trapezium = Som van alle vier zijden
Gebied van trapeziumformule
Trapezium heeft twee parallelle zijden, respectievelijk a en b, en de hoogte is h.
Nu kan de oppervlakte van het trapezium worden berekend door het gemiddelde van de bases te vinden en het resultaat ervan te vermenigvuldigen met de hoogte. Vandaar,
Gebied van Trapezium = ((a +b)/2) × u
waar,
- A En B zijn basen van trapezium
- H is Hoogte
Gebied van gelijkbenig trapezium
Laat a en b de lengte zijn van evenwijdige zijden van een trapezium ABCD, waarbij a en b de basis zijn van het trapezium en a>b.
Omdat het een gelijkbenig trapezium is, is c de lengte van beide niet-parallelle zijden en is h de hoogte van het trapezium.
Nu AB = a, CD = b, BC = AD = c
In Rechte driehoek , AED
Lengte van loodlijn, h = √(c 2 – (ab) 2 ) [gebruik makend van De stelling van Pythagoras ]….(1)
Nu,
Oppervlakte = ½ × som van parallelle zijden × hoogte van trapezium
Oppervlakte = ½ × (a+b) × h
Vergelijking gebruiken (1)
Gebied van gelijkbenig trapezium = 1/2 × [√(ca 2 – (ab) 2 ) (a+b)]
Omtrek van trapeziumformule
De omtrek van een trapezium wordt bepaald door de som van alle zijden te berekenen. Vandaar,
Omtrek van trapezium = AB + BC + CD + AD
waar, AB, BC, CD En ADVERTENTIE zijn zijden van trapezium
Omtrek van gelijkbenig trapezium
Als in een gelijkbenig trapezium a en b de lengtes zijn van evenwijdige zijden, dat wil zeggen de bases, en c de lengte is van twee gelijke niet-parallelle zijden, dan wordt de omtrek gegeven door:
Omtrek = a + b + 2c
waar,
alfabet en cijfers
- A , B zijn basen van trapezium
- C is Gelijke Kant van Trapezium
Verschil tussen trapezium en trapezium
Over het algemeen zijn zowel Trapezium als Trapezium hetzelfde, maar het verschil ligt in het land van herkomst.
- Trapezium is van Britse oorsprong, het is een vierzijdige veelhoek en een tweedimensionale figuur en heeft precies één paar evenwijdige zijden tegenover elkaar. In India volgen we Brits-Engels en daarom wordt het woord Trapezium gebruikt.
- Trapezium is van Amerikaanse oorsprong, het is ook een vierzijdige veelhoek met één paar evenwijdige zijden tegenover elkaar. Parallelle zijden zijn de basis en nog twee niet-parallelle zijden worden de benen van het trapezium genoemd.
Hoeken van trapezium
Trapezium is een vierhoek en de som van alle hoeken van een vierhoek is 360 graden. De som van alle binnenhoeken van het trapezium is dus 360 graden.
Voor elk regelmatig trapezium, d.w.z. het trapezium waarin niet-parallelle zijden gelijk zijn aan de aangrenzende hoeken gevormd tussen de evenwijdige lijn en de niet-parallelle lijn, is gelijk. De som van deze twee hoeken is dus aanvullend.
Laten we een voorbeeld nemen om dit concept voor een gelijkbenig trapezium ABCD te ondersteunen als AB evenwijdig is aan CD en AD gelijk is aan CD, dan weten we dat ∠A = ∠B en ∠C = ∠D dan,
∠A + ∠B + ∠C + ∠D = 360°
Hier geldt ∠A = ∠B en ∠C = ∠D
∠A + ∠A + ∠C + ∠C = 360°
2(∠A + ∠C) = 360°
(∠A + ∠C) = 180°
Op dezelfde manier geldt (∠B + ∠D) = 180°
Diagonaal van Trapezium
Trapezium is een speciaal type vierhoek; trapezium heeft dus ook twee diagonalen. De diagonalen van een trapezium hebben geen gelijke lengte, in tegenstelling tot sommige andere vierhoeken zoals rechthoeken of parallellogrammen. Diagonalen van trapezium hebben geen gelijke lengte en de lengte van de diagonalen hangt af van de lengte van de basis en de hoeken van het trapezium.
Voorbeeld: Voor een gelijkbenig trapezium ABCD is de basishoek ∠A 80° en zoek dan de andere hoek ∠C.
We weten dat voor een gelijkbenig trapezium ABCD,
(∠A + ∠C) = 180°
Gegeven, ∠A = 80°
Nu is 80° + ∠C = 180°
∠C = 180 – 80
∠C = 100°
De vereiste hoek ∠C is dus 100°
Trapeziumformules - Oppervlakte en omtrek van trapezium
Formules met betrekking tot trapezium zijn samengevat in de volgende tabel:
| Eigendom | Formule |
|---|---|
| Gebied | 1/2 × ( A + B )× H |
| Gebied (gelijkbenig trapezium) | 1/2 × [√(c2– (ab)2) (a+b)] |
| Omtrek | A + B + C + D |
| Omtrek (gelijkbenig trapezium) | A + B + 2 C |
| Mediaan | (A + b)/2 |
Mensen lezen ook:
- Ruit
- Driehoek
- Wat is de formule om het trapeziumgebied te vinden?
Trapezium-voorbeelden
Voorbeeld 1: Zoek de vierde zijde van het trapezium, als de andere drie zijden 8 cm, 12 cm en 16 cm zijn, en de omtrek 40 cm is.
Oplossing:
De omtrek wordt gegeven als de som van al zijn zijden. Laat de lengte o onbekend 'x' eenheden zijn.
Omtrek = 40
40 = 8 + 12 + 16 + x
x = 40 – (8 + 12 + 16)
= 4 cm
De lengte van de onbekende zijde is dus 4 cm
Voorbeeld 2: Een trapezium heeft evenwijdige zijden met een lengte van 15 cm en 11 cm, en niet-parallelle zijden met een lengte van elk 5 cm. Bereken de omtrek van de trapezium.
Oplossing:
Het is een gelijkbenig trapezium omdat duidelijk wordt vermeld dat niet-parallelle zijden met een lengte van elk 5 cm gelijk zijn.
Volgens Gelijkbenig Trapezium als twee niet-parallelle zijden van Trapezium even lang zijn, staat het bekend als Gelijkbenig Trapezium.
Gegeven,
- a = 15 cm
- b = 11 cm
- c = 5 cm
Omtrek = a + b + 2c
P = 15 + 11 + 2(5)
P = 15 + 11 + 10
P = 36 cm
Voorbeeld 3: Vind de omtrek van een trapezium waarvan de zijden 12 cm, 14 cm, 16 cm en 18 cm zijn.
Oplossing:
P = Som van alle zijden
P = 12 + 14 + 16 + 18
P = 60 cm
De omtrek van het trapezium is dus 60 cm
Voorbeeld 4: Zoek het gebied van het trapezium, waarin de som van de evenwijdige zijden 60 cm is en de hoogte 10 cm.
Oplossing:
Gegeven,
- Som van parallelle zijden 60 cm
- hoogte, h = 10 cm
Oppervlakte van trapezium, A = 1/2 × Som van parallelle zijden × Afstand tussen parallelle zijden
Gegeven waarden vervangen,
EEN =1/2×60×10
EEN = 30×10
A = 300cm2
Daarom is de oppervlakte van het trapezium = 300 cm2
Oefenproblemen met trapezium in wiskunde
1. Bereken de oppervlakte van een trapezium met een basis van 10 cm en 15 cm en een hoogte van 6 cm.
2. Een trapezium heeft een oppervlakte van 54 vierkante meter. Als een van de basissen 12 meter lang is en de hoogte 6 meter, zoek dan de lengte van de andere basis.
3. Bereken de omtrek van een trapezium met basissen van 8 cm en 14 cm, en niet-parallelle zijden van 5 cm en 7 cm.
4. Bepaal de lengte van het middensegment in een trapezium waarbij de basis 18 cm en 30 cm meet.
5. In een gelijkbenig trapezium zijn de hoeken aan één basis elk 45 graden. Zoek de afmetingen van de hoeken aan de andere basis. Neem aan dat het trapezium geen rechts trapezium is.
Samenvatting – Trapezium in wiskunde
Een trapezium is een vierzijdige veelhoek, of vierhoek, gekenmerkt door één paar evenwijdige zijden, de zogenaamde bases, terwijl de andere twee zijden, ook wel benen genoemd, niet evenwijdig zijn. Het trapezium komt veel voor in alledaagse voorwerpen zoals tafels en valt op door zijn geometrische eigenschappen: het heeft een hoogte, de loodrechte afstand tussen de bases, en een mediaan die de middelpunten van de niet-parallelle zijden verbindt en evenwijdig is aan de bases.
De oppervlakte van een trapezium wordt berekend door de lengtes van de bases te middelen en te vermenigvuldigen met de hoogte, terwijl de omtrek de som is van al zijn zijden. Met verschillende classificaties zoals ongelijkbenige, gelijkbenige en rechte trapeziums, elk met unieke zij- en hoekeigenschappen, zijn trapeziums van fundamenteel belang in zowel praktische toepassingen als de geometrische theorie.
Veelgestelde vragen over Trapezium in wiskunde
Wat is trapeziumvorm?
Trapezium is een vierhoek waarin een paar lijnen altijd evenwijdig zijn. Het lijkt op de vorm van een tafel. De naam is ontleend aan het Griekse woord trapeze, wat tafel betekent.
Hoeveel soorten trapezium?
Er zijn twee soorten trapezium,
- Regelmatig trapezium: Waarbij het andere paar lijnen gelijk is.
- Onregelmatig trapezium: Waarin het andere paar lijnen niet gelijk is.
Hoeveel parallelle zijden heeft een trapezium?
We weten dat trapezium een vierhoek is met één paar evenwijdige zijden. Een trapezium heeft dus een paar evenwijdige lijnen (zijkanten).
Kan een trapezium als een vierhoek worden beschouwd?
A heeft vier zijden, vier hoekpunten en vier hoeken. Daarom kan het als een vierhoek worden beschouwd; de som van alle vier de binnenhoeken van een trapezium is 360 graden.
Kan een vierkant een trapezium worden genoemd?
Een trapezium is een vierhoek met slechts één paar evenwijdige zijden en de andere twee zijden zijn niet evenwijdig. Maar in het geval van een vierkant heeft het twee paar evenwijdige zijden en kan het daarom niet als een trapezium worden beschouwd.
Zijn de diagonalen van een trapezium altijd gelijk?
Diagonalen van een trapezium zijn mogelijk niet gelijk. Bij een regelmatige veelhoek zijn de diagonalen gelijk, maar bij een onregelmatige veelhoek is dit niet het geval.
Wat zijn eigenschappen van een trapezium?
5 eigenschappen van een Trapezium zijn:
- In trapezium zijn de bases evenwijdig aan elkaar.
- Een trapezium heeft aanvullende aangrenzende hoeken.
- Slechts één paar tegenoverliggende zijden is evenwijdig.
- De som van alle binnenhoeken in een trapezium is altijd 360°.
- De lijn die het middelpunt van niet-parallelle zijden verbindt, is altijd evenwijdig aan de basis.
