Er zijn talloze manieren om de prestaties van een classificator te evalueren. In dit artikel introduceren we de Precision-Recall Curve en onderzoeken we verder het verschil tussen twee populaire methoden voor prestatierapportage: Precision-Recall (PR) Curve en Ontvanger bedrijfskarakteristiek (ROC) Kromme. ROC Curve wordt al besproken in de artikel . Laten we kort begrijpen wat een Precision-Recall-curve is.
Wat is precisie en herinnering?
Precisie
- De verhouding tussen correct voorspelde positieve waarnemingen en alle voorspelde positieve waarnemingen staat bekend als precisie.
- Het meet hoe goed het model de positieve uitkomsten voorspelt.
- De precisieformule is:
- Precisie houdt zich bezig met de kwaliteit van positieve voorspellingen. Een hoge precisie geeft aan dat het model een laag percentage valse positieven heeft.
Herinneren
- De verhouding tussen correct voorspelde positieve waarnemingen en het totale aantal daadwerkelijke positieve waarnemingen staat bekend als herinnering.
- Het meet hoe goed het model elk relevant geval kan vastleggen.
- Recall wordt berekend met behulp van deze formule:
- Recall houdt zich bezig met de hoeveelheid relevante instanties die door het model worden vastgelegd. Een hoge terugroepactie geeft aan dat het model weinig fout-negatieven heeft.
In termen van empirische interpretatie is een verwarringsmatrix bestaande uit vier essentiële termen het nuttigste hulpmiddel voor het begrijpen van precisie en herinnering:
- True Positive (TP): Het aantal positieve klasse-instanties dat nauwkeurig is geïdentificeerd
- False Positive (FP): Het aantal negatieve klasse-instanties dat ten onrechte wordt geïdentificeerd als positieve klasse-instanties, staat bekend als False Positive (FP).
- True Negative (TN): Het aantal negatieve klasse-instanties dat nauwkeurig is geïdentificeerd
- Vals-negatief (FN): telling van positieve klasse-instanties die ten onrechte zijn geclassificeerd als negatieve klasse-instanties (False-negatief of FN)
Precision Recall (PR)-curve in machinaal leren
Precisie is het aandeel van juist positieve classificaties (echt positief) gedeeld door het totale aantal voorspelde positieve classificaties die zijn gemaakt (waar positief + vals positief). Herinneren is het aandeel van juist positieve classificaties (echt positief) gedeeld door het totale aantal werkelijk positieve classificaties (waar positief + vals negatief).
Een PR-curve is eenvoudigweg een grafiek met precisiewaarden op de y-as en Recall-waarden op de x-as. Met andere woorden, de PR-curve bevat
- Het is belangrijk op te merken dat precisie ook wel de positief voorspellende waarde (PPV) wordt genoemd.
- De terugroepactie wordt ook wel Gevoeligheid, Hit Rate of True Positive Rate (TPR) genoemd.
De onderstaande afbeelding toont een vergelijking van voorbeeld-PR- en ROC-curven. 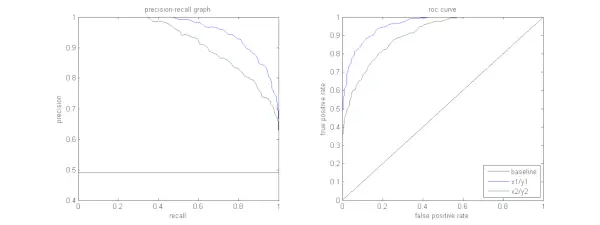
Een precisie-herinneringscurve interpreteren
Het is gewenst dat het algoritme zowel een hoge nauwkeurigheid als een hoge herinneringswaarde heeft. Bij de meeste machine learning-algoritmen is er echter vaak sprake van een afweging tussen deze twee. Een goede PR-curve heeft een grotere AUC (gebied onder de curve) . In de bovenstaande afbeelding presteert de classificator die overeenkomt met de blauwe lijn beter dan de classificator die overeenkomt met de groene lijn. Het is belangrijk op te merken dat de classificator met een hogere AUC op de ROC-curve zal ook altijd een hogere AUC op de PR-curve hebben. Overweeg een algoritme dat classificeert of een document wel of niet tot de categorie Sportnieuws behoort. Stel dat er twaalf documenten zijn, met de volgende grondwaarheid (werkelijk) en classificatie-uitvoerklasselabels.
| Document-ID | Grond waarheid | Classificatie-uitvoer |
|---|---|---|
| D1 | Sport | Sport |
| D2 | Sport | Sport |
| D3 | Niet sport | Sport |
| D4 | Sport | Niet sport |
| D5 | Niet sport | Niet sport |
| D6 | Sport | Niet sport |
| D7 | Niet sport | Sport |
| D8 | Niet sport | Niet sport |
| D9 | Niet sport | Niet sport |
| D10 | Sport | Sport |
| D11 | Sport | Sport |
| D12 | Sport | Niet sport |
Laten we nu de TP-, TN-, FP- en FN-waarden vinden.
Laten we een voorbeeld gebruiken met documenten die zijn geclassificeerd als Sport of Niet-sport om de definities van True Positives (TP), True Negatives (TN), False Positives (FP) en False Negatives (FN) beter uit te leggen in de context van classificatie:
Echte positieven (TP): Documenten die nauwkeurig als Sport waren gecategoriseerd en die feitelijk over sport gingen. Documenten D1, D2, D10 en D11 zijn in dit scenario exemplaren van TP.
Echte negatieven (TN): Echte negatieven zijn die gevallen waarin het document terecht werd bestempeld als Niet-sport, ook al had het niets met sport te maken. In dit geval wordt TN aangetoond door de documenten D5, D8 en D9.
Valse positieven (FP): Documenten die ten onrechte als sport werden gecategoriseerd, ook al hadden ze niets met sport te maken. Hier zijn enkele FP-voorbeelden, documenten D3 en D7.
Valse negatieven (FN): Voorbeelden van documenten die ten onrechte werden bestempeld als Geen sport, maar in werkelijkheid over sport gingen. Documenten D4, D6 en D12 zijn in dit geval FN-voorbeelden.
Gezien deze tellingen: Stad =4, TN =3, FP =2, FN =3
Ten slotte worden precisie en terugroeping als volgt berekend:
Precision = frac{TP}{TP+FP} = frac{4}{6} = frac{2}{3}
Recall = frac{TP}{TP+FN} = frac{4}{7} Hieruit volgt dat de terugroepactie 4/7 is als de precisie 2/3 is. Met andere woorden: van alle gevallen waarvan werd verwacht dat ze positief zouden zijn, werd tweederde nauwkeurig geclassificeerd (precisie), en van alle gevallen die daadwerkelijk positief waren, kon het model vier zevende ervan vastleggen (herinnering).
Door verschillende drempels in te stellen, krijgen we meerdere van dergelijke precisie-herinneringsparen. Door meerdere van dergelijke P-R-paren uit te zetten met een waarde variërend van 0 tot 1, krijgen we een PR-curve.
Heeft u een PR-curve nodig als de ROC-curve bestaat?
De PR-curve is met name nuttig bij het rapporteren van Information Retrieval-resultaten.
Bij het ophalen van informatie wordt gezocht in een verzameling documenten om de documenten te vinden die relevant zijn voor een bepaalde gebruikersquery. Stel bijvoorbeeld dat de gebruiker een zoekopdracht Pink Elephants invoert. De zoekmachine bladert door miljoenen documenten (met behulp van enkele geoptimaliseerde algoritmen) om een handvol relevante documenten op te halen. Daarom kunnen we veilig aannemen dat nr. van relevante documenten zal veel minder zijn vergeleken met nr. van niet-relevante documenten.
In dit scenario,
- TP = Aantal opgehaalde documenten die relevant zijn (goede resultaten).
- FP = Aantal opgehaalde documenten die niet-relevant zijn (nep-zoekresultaten).
- TN = Aantal niet-opgehaalde documenten die niet-relevant zijn.
- FN = Aantal niet-opgehaalde documenten die relevant zijn (goede documenten die we hebben gemist).
ROC-curve is een grafiek met Recall = TPR =
verschil tussen bedrijf en bedrijf
Verder helpt FPR ons niet om een ophaalsysteem goed te evalueren, omdat we ons meer willen concentreren op de opgehaalde documenten, en niet op de niet-opgehaalde documenten. PR-curve helpt dit probleem op te lossen. PR-curve heeft de Recall-waarde (TPR) op de x-as, en precisie =
Wanneer ROC versus Precision-Recall-curven gebruiken?
ROC (Receiver Operating Characteristic)-curven zijn geschikt als de klassenverdeling evenwichtig is en valse positieven en valse negatieven vergelijkbare gevolgen hebben. Ze geven de wisselwerking weer tussen gevoeligheid en specificiteit. Daarentegen verdienen Precision-Recall-curven de voorkeur bij het omgaan met onevenwichtige datasets, waarbij de nadruk ligt op positieve klassevoorspellingsprestaties.
Precision-Recall biedt inzicht in het vermogen van het model om positieve gevallen correct te classificeren. De keuze tussen ROC en Precision-Recall hangt af van de specifieke behoeften van het probleem, waarbij het belang wordt benadrukt van het begrijpen van de gegevensdistributie en de gevolgen van verschillende soorten fouten.
Implementatie van basiscode voor Precision-Recall Curve
Noodzakelijke bibliotheken importeren
Deze coderegels importeren de Python-bibliotheken en modules die nodig zijn om een precisie-recall-curve mee te genereren sci-kit-leren en visualiseer de resultaten met Matplotlib . Matplotlib is een populaire Python-plotbibliotheek en pyplot biedt een eenvoudige interface voor het maken van verschillende soorten plots en diagrammen. Logistieke regressie is een populair classificatiealgoritme voor binaire en multiclass classificatietaken. De precisie-herinneringscurve en AUC zijn populaire evaluatiestatistieken binaire classificatie problemen, vooral als het gaat om onevenwichtige datasets.
Python3 import matplotlib.pyplot as plt from sklearn.datasets import make_classification from sklearn.model_selection import train_test_split from sklearn.linear_model import LogisticRegression from sklearn.metrics import precision_recall_curve, auc> Dataset gebruikt
Deze code genereert een synthetische dataset voor een binair classificatieprobleem met behulp van de ‘make_classification’-functie van sci-kit-learn.
Python3 # Generate a synthetic dataset X, y = make_classification( n_samples=1000, n_features=20, n_classes=2, random_state=42)> Trein- en testsplitsing
De train_test_split De functie in scikit-learn wordt in dit codefragment gebruikt om de eerder gegenereerde synthetische dataset (X en y) op te splitsen in trainings- en testsets. Deze splitsing is een cruciale stap bij het evalueren van machine learning-modellen. Het model wordt getraind op de X_train- en y_train-gegevens voordat het wordt getest op de X_test- en y_test-gegevens om te zien hoe goed het presteert op onzichtbare monsters. De train_test_split-functie scheidt trainings- en testsets en zorgt ervoor dat de prestaties van het model de generalisatie ervan naar nieuwe, voorheen onzichtbare gegevens weerspiegelen.
Python3 # Split the dataset into training and testing sets X_train, X_test, y_train, y_test = train_test_split( X, y, test_size=0.2, random_state=42)> Model gebouw
Hier gebruiken we logistische regressie om het model te trainen op de trainingsdataset. Logistische regressie, een populair algoritme voor binaire classificatie, wordt geïmplementeerd door de sci-kit-learn-klasse LogisticRegression.
Python3 # Train a logistic regression model (you can replace this with your own classifier) model = LogisticRegression() model.fit(X_train, y_train)> Modelvoorspelling
Deze berekeningen geven doorgaans precisie- en herinneringswaarden voor verschillende beslissingsdrempels, die u kunt gebruiken om een precisie-herinneringscurve te tekenen of het relatieve belang van precisie en herinnering op verschillende tijdstippen te onderzoeken. En het berekenen van de Gebied onder de curve (AUC) voor de precisie-terugroepcurve.
Python3 # Predict probabilities for positive class y_scores = model.predict_proba(X_test)[:, 1] # Calculate precision and recall precision, recall, thresholds = precision_recall_curve(y_test, y_scores) # Calculate Area Under the Curve (AUC) for precision-recall curve auc_score = auc(recall, precision)> PR-curve uitzetten
Dit codeblok biedt een standaardmethode voor het visualiseren van de precisie-herroepcurve en laat u de afweging tussen precisie en terugroepen evalueren bij verschillende beslissingsdrempels. De algehele prestaties van het model op de precisie-terugroepcurve worden samengevat door de AUC-score die in de legenda wordt weergegeven.
Python3 # Plot precision-recall curve plt.figure(figsize=(8, 6)) plt.plot(recall, precision, label=f'Precision-Recall Curve (AUC = {auc_score:.2f})') plt.xlabel('Recall') plt.ylabel('Precision') plt.title('Precision-Recall Curve') plt.legend() plt.show()> Uitvoer :

Precisie-herinneringscurve
Veelgestelde vragen (FAQ's)
V. Wat is precisie?
De verhouding tussen nauwkeurig voorspelde positieve waarnemingen en het totale aantal voorspelde positieve waarnemingen staat bekend als precisie. Het meet hoe goed het model de positieve uitkomsten voorspelt. Het volgende is de precisieformule:
Precision = frac{True Positives}{True Positives + False Positives}
V. Wat is terugroepen?
Recall is de verhouding tussen correct voorspelde positieve waarnemingen en het totale aantal daadwerkelijke positieve waarnemingen. Het wordt ook wel gevoeligheid of echt positief percentage genoemd. Het beoordeelt hoe goed het model elk relevant geval kan vastleggen. Recall wordt berekend met behulp van de volgende formule:
Precision = frac{True Positives}{True Positives + False Negatives}
V. Waarom hebben we precisie en herinnering nodig?
Om de prestaties van een classificator bij binaire classificatieproblemen en classificatieproblemen met meerdere klassen te beoordelen, worden twee evaluatiestatistieken gebruikt: precisie en herinnering. De nauwkeurigheid van positieve voorspellingen wordt gemeten door precisie, en de volledigheid van positieve voorspellingen wordt gemeten door terugroeping.
V. Wat is de afweging tussen terugroepen en precisie?
Herinnering en precisie zijn vaak compromissen. De herinnering kan eronder lijden naarmate de nauwkeurigheid toeneemt, en omgekeerd. Door de balk voor het identificeren van een positief exemplaar te veranderen, kan deze afweging worden beheerd. Omgekeerd resulteert een lagere drempel in een lagere herinnering maar een hogere precisie. De beslissing tussen herinnering en precisie is gebaseerd op de bijzonderheden van het gegeven probleem.
V. Wat is de F1-score en hoe verhoudt deze zich tot precisie en herinnering?
Het harmonische gemiddelde van herinnering en precisie staat bekend als de F1-score. Het biedt een eerlijke meting die rekening houdt met zowel valse positieven als valse negatieven. De F1-score wordt berekend met behulp van de volgende formule:
F1-Score = frac{2 imes Precision imes Recall}{Precision + Recall} De F1-score is vooral handig wanneer precisie en herinnering uit balans zijn en een evenwicht tussen beide gewenst is.
