Logistieke regressie is een begeleid machine learning-algoritme gebruikt voor classificatie taken waarbij het doel is om de waarschijnlijkheid te voorspellen dat een instantie tot een bepaalde klasse behoort of niet. Logistieke regressie is een statistisch algoritme dat de relatie tussen twee gegevensfactoren analyseert. Het artikel onderzoekt de fundamenten van logistische regressie, de typen en implementaties ervan.

Inhoudsopgave

• Wat is logistieke regressie?
• Logistieke functie – Sigmoid-functie
• Soorten logistieke regressie
• Aannames van logistieke regressie
• Hoe werkt logistieke regressie?
• Code-implementatie voor logistieke regressie
• Afweging tussen precisie en terugroepen bij het instellen van logistieke regressiedrempels
• Hoe het logistieke regressiemodel evalueren?
• Verschillen tussen lineaire en logistieke regressie

Wat is logistieke regressie?

Logistieke regressie wordt gebruikt voor binair classificatie waar wij gebruiken sigmoïde functie , die invoer als onafhankelijke variabelen gebruikt en een waarschijnlijkheidswaarde tussen 0 en 1 oplevert.

We hebben bijvoorbeeld twee klassen, Klasse 0 en Klasse 1, als de waarde van de logistieke functie voor een invoer groter is dan 0,5 (drempelwaarde), dan behoort deze tot Klasse 1, anders behoort deze tot Klasse 0. Er wordt naar verwezen als regressie omdat deze is het verlengstuk van lineaire regressie maar wordt vooral gebruikt voor classificatieproblemen.

Belangrijkste punten:

• Logistische regressie voorspelt de output van een categorisch afhankelijke variabele. Daarom moet de uitkomst een categorische of discrete waarde zijn.
• Het kan Ja of Nee zijn, 0 of 1, waar of Onwaar, etc., maar in plaats van de exacte waarde 0 en 1 te geven, geeft het de probabilistische waarden die tussen 0 en 1 liggen.
• Bij logistieke regressie passen we, in plaats van een regressielijn aan te passen, een S-vormige logistieke functie toe, die twee maximale waarden voorspelt (0 of 1).

Logistieke functie – Sigmoid-functie

• De sigmoïdefunctie is een wiskundige functie die wordt gebruikt om de voorspelde waarden aan waarschijnlijkheden toe te wijzen.
• Het koppelt elke reële waarde aan een andere waarde binnen een bereik van 0 en 1. De waarde van de logistische regressie moet tussen 0 en 1 liggen, wat niet verder kan gaan dan deze limiet, dus vormt het een curve zoals de S-vorm.
• De S-vormcurve wordt de Sigmoid-functie of de logistieke functie genoemd.
• Bij logistieke regressie gebruiken we het concept van de drempelwaarde, die de waarschijnlijkheid van 0 of 1 definieert. Zoals waarden boven de drempelwaarde naar 1 neigen, en een waarde onder de drempelwaarden naar 0 neigt.

Soorten logistieke regressie

Op basis van de categorieën kan logistieke regressie in drie typen worden ingedeeld:

1. Binomiaal: Bij binomiale logistieke regressie kunnen er slechts twee mogelijke typen afhankelijke variabelen zijn, zoals 0 of 1, geslaagd of mislukt, enz.
2. Multinomiaal: Bij multinomiale logistieke regressie kunnen er 3 of meer mogelijke ongeordende typen van de afhankelijke variabele zijn, zoals kat, hond of schaap
3. Ordinaal: Bij ordinale logistische regressie kunnen er drie of meer mogelijke geordende typen afhankelijke variabelen zijn, zoals laag, gemiddeld of hoog.

Aannames van logistieke regressie

We zullen de aannames van logistieke regressie onderzoeken, omdat het begrijpen van deze aannames belangrijk is om ervoor te zorgen dat we het model op de juiste manier toepassen. De veronderstelling omvat:

1. Onafhankelijke observaties: Elke observatie is onafhankelijk van de andere. wat betekent dat er geen correlatie bestaat tussen invoervariabelen.
2. Binaire afhankelijke variabelen: Er wordt van uitgegaan dat de afhankelijke variabele binair of dichotoom moet zijn, wat betekent dat deze slechts twee waarden kan aannemen. Voor meer dan twee categorieën worden SoftMax-functies gebruikt.
3. Lineariteitsrelatie tussen onafhankelijke variabelen en log odds: De relatie tussen de onafhankelijke variabelen en de log odds van de afhankelijke variabele moet lineair zijn.
4. Geen uitschieters: Er mogen geen uitschieters in de dataset voorkomen.
5. Grote steekproefomvang: De steekproefomvang is voldoende groot

Terminologieën die betrokken zijn bij logistieke regressie

Hier zijn enkele veel voorkomende termen die betrokken zijn bij logistische regressie:

• Onafhankelijke variabelen: De invoerkenmerken of voorspellende factoren die worden toegepast op de voorspellingen van de afhankelijke variabele.
• Afhankelijke variabele: De doelvariabele in een logistisch regressiemodel, die we proberen te voorspellen.
• Logistieke functie: De formule die wordt gebruikt om weer te geven hoe de onafhankelijke en afhankelijke variabelen zich tot elkaar verhouden. De logistieke functie transformeert de invoervariabelen in een waarschijnlijkheidswaarde tussen 0 en 1, die de waarschijnlijkheid weergeeft dat de afhankelijke variabele 1 of 0 is.
• Kansen: Het is de verhouding tussen iets dat gebeurt en iets dat niet gebeurt. het verschilt van waarschijnlijkheid, aangezien de waarschijnlijkheid de verhouding is tussen iets dat gebeurt en alles wat mogelijk zou kunnen gebeuren.
• Log-odds: De log-odds, ook wel de logit-functie genoemd, is de natuurlijke logaritme van de odds. Bij logistische regressie worden de log odds van de afhankelijke variabele gemodelleerd als een lineaire combinatie van de onafhankelijke variabelen en het snijpunt.
• Coëfficiënt: De geschatte parameters van het logistieke regressiemodel laten zien hoe de onafhankelijke en afhankelijke variabelen zich tot elkaar verhouden.
• Onderscheppen: Een constante term in het logistische regressiemodel, die de log-odds vertegenwoordigt wanneer alle onafhankelijke variabelen gelijk zijn aan nul.
• Schatting van de maximale waarschijnlijkheid : De methode die wordt gebruikt om de coëfficiënten van het logistische regressiemodel te schatten, waardoor de waarschijnlijkheid van het waarnemen van de gegevens op basis van het model wordt gemaximaliseerd.

Hoe werkt logistieke regressie?

Het logistische regressiemodel transformeert de lineaire regressie functie continue waarde-uitvoer in categorische waarde-uitvoer met behulp van een sigmoïde functie, die elke reeks onafhankelijke variabelen met reële waarde in kaart brengt die wordt ingevoerd in een waarde tussen 0 en 1. Deze functie staat bekend als de logistieke functie.

Laat de onafhankelijke invoerfuncties zijn:

X = egin{bmatrix} x_{11} & … & x_{1m} x_{21} & … & x_{2m} vdots & ddots & vdots x_{n1} & … & x_{nm} end{bmatrix}

pd.merge

en de afhankelijke variabele is Y met alleen een binaire waarde, dat wil zeggen 0 of 1.

Y = egin{cases} 0 & ext{ if } Class;1 1 & ext{ if } Class;2 end{cases}

pas vervolgens de multi-lineaire functie toe op de invoervariabelen X.

z = left(sum_{i=1}^{n} w_{i}x_{i} ight) + b

Hierx_i is de i-de waarneming van X,w_i = [w_1, w_2, w_3, cdots,w_m] is de gewichten of coëfficiënt, en b is de bias-term, ook bekend als intercept. dit kan eenvoudigweg worden weergegeven als het puntproduct van gewicht en bias.

z = wcdot X +b

wat we hierboven hebben besproken, is de lineaire regressie .

Sigmoïde-functie

Nu gebruiken wij de sigmoïde functie waarbij de invoer z zal zijn en we de waarschijnlijkheid tussen 0 en 1 vinden, dat wil zeggen voorspelde y.

sigma(z) = frac{1}{1-e^{-z}}

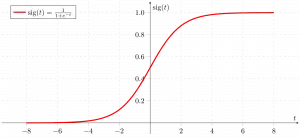
Sigmoïde functie

Zoals hierboven weergegeven, converteert de figuur-sigmoïdefunctie de continue variabele gegevens naar de waarschijnlijkheid dat wil zeggen tussen 0 en 1.

• sigma(z) neigt naar 1 alsz ightarrowinfty
• sigma(z) neigt naar 0 alsz ightarrow-infty
• sigma(z) altijd begrensd tussen 0 en 1

waarbij de waarschijnlijkheid om een ​​klasse te zijn kan worden gemeten als:

P(y=1) = sigma(z) P(y=0) = 1-sigma(z)

Logistieke regressievergelijking

Het vreemde is de verhouding tussen iets dat gebeurt en iets dat niet gebeurt. het verschilt van waarschijnlijkheid, aangezien de waarschijnlijkheid de verhouding is tussen iets dat gebeurt en alles wat mogelijk zou kunnen gebeuren. zo vreemd zal zijn:

frac{p(x)}{1-p(x)} = e^z

Natuurlijke aanmelding oneven toepassen. dan zal log oneven zijn:

egin{aligned} log left[frac{p(x)}{1-p(x)} ight] &= z log left[frac{p(x)}{1-p(x)} ight] &= wcdot X +b frac{p(x)}{1-p(x)}&= e^{wcdot X +b} ;;cdots ext{Exponentiate both sides} p(x) &=e^{wcdot X +b}cdot (1-p(x)) p(x) &=e^{wcdot X +b}-e^{wcdot X +b}cdot p(x)) p(x)+e^{wcdot X +b}cdot p(x))&=e^{wcdot X +b} p(x)(1+e^{wcdot X +b}) &=e^{wcdot X +b} p(x)&= frac{e^{wcdot X +b}}{1+e^{wcdot X +b}} end{aligned}

dan zal de uiteindelijke logistische regressievergelijking zijn:

p(X;b,w) = frac{e^{wcdot X +b}}{1+e^{wcdot X +b}} = frac{1}{1+e^{-wcdot X +b}}

Waarschijnlijkheidsfunctie voor logistieke regressie

De voorspelde kansen zijn:

ex van gebruikersnaam

• voor y=1 De voorspelde kansen zijn: p(X;b,w) = p(x)
• voor y = 0 De voorspelde kansen zijn: 1-p(X;b,w) = 1-p(x)

L(b,w) = prod_{i=1}^{n}p(x_i)^{y_i}(1-p(x_i))^{1-y_i}

Aan beide kanten natuurlijke boomstammen nemen

egin{aligned}log(L(b,w)) &= sum_{i=1}^{n} y_ilog p(x_i);+; (1-y_i)log(1-p(x_i)) &=sum_{i=1}^{n} y_ilog p(x_i)+log(1-p(x_i))-y_ilog(1-p(x_i)) &=sum_{i=1}^{n} log(1-p(x_i)) +sum_{i=1}^{n}y_ilog frac{p(x_i)}{1-p(x_i} &=sum_{i=1}^{n} -log1-e^{-(wcdot x_i+b)} +sum_{i=1}^{n}y_i (wcdot x_i +b) &=sum_{i=1}^{n} -log1+e^{wcdot x_i+b} +sum_{i=1}^{n}y_i (wcdot x_i +b) end{aligned}

Gradiënt van de logwaarschijnlijkheidsfunctie

Om de maximale waarschijnlijkheidsschattingen te vinden, differentiëren we naar:

egin{aligned} frac{partial J(l(b,w)}{partial w_j}&=-sum_{i=n}^{n}frac{1}{1+e^{wcdot x_i+b}}e^{wcdot x_i+b} x_{ij} +sum_{i=1}^{n}y_{i}x_{ij} &=-sum_{i=n}^{n}p(x_i;b,w)x_{ij}+sum_{i=1}^{n}y_{i}x_{ij} &=sum_{i=n}^{n}(y_i -p(x_i;b,w))x_{ij} end{aligned}

Code-implementatie voor logistieke regressie

Binomiale logistieke regressie:

Doelvariabelen kunnen slechts 2 mogelijke typen hebben: 0 of 1, wat winst versus verlies kan vertegenwoordigen, geslaagd versus mislukt, dood versus levend, enz.. In dit geval worden sigmoïde functies gebruikt, die hierboven al zijn besproken.

semantische fout

Importeren van noodzakelijke bibliotheken op basis van de vereisten van het model. Deze Python-code laat zien hoe u de borstkankerdataset kunt gebruiken om een ​​logistiek regressiemodel voor classificatie te implementeren.

Uitvoer :

Nauwkeurigheid van het logistieke regressiemodel (in %): 95,6140350877193

Multinomiale logistieke regressie:

De doelvariabele kan drie of meer mogelijke typen hebben die niet geordend zijn (d.w.z. typen hebben geen kwantitatieve betekenis), zoals ziekte A versus ziekte B versus ziekte C.

In dit geval wordt de softmax-functie gebruikt in plaats van de sigmoïdefunctie. Softmax-functie voor K-klassen wordt:

ext{softmax}(z_i) =frac{ e^{z_i}}{sum_{j=1}^{K}e^{z_{j}}}

Hier, K vertegenwoordigt het aantal elementen in de vector z, en i, j itereert over alle elementen in de vector.

Dan is de kans voor klasse c:

P(Y=c | overrightarrow{X}=x) = frac{e^{w_c cdot x + b_c}}{sum_{k=1}^{K}e^{w_k cdot x + b_k}}

Bij multinomiale logistieke regressie kan de uitvoervariabele het volgende hebben meer dan twee mogelijke discrete uitgangen . Denk aan de Digit-gegevensset.

Uitgang:

Nauwkeurigheid van het logistieke regressiemodel (in%): 96,52294853963839

Hoe het logistieke regressiemodel evalueren?

We kunnen het logistische regressiemodel evalueren met behulp van de volgende statistieken:

• Nauwkeurigheid: Nauwkeurigheid geeft het aandeel correct geclassificeerde gevallen weer.
  Accuracy = frac{True , Positives + True , Negatives}{Total}

• Precisie: Precisie richt zich op de nauwkeurigheid van positieve voorspellingen.
  Precision = frac{True , Positives }{True, Positives + False , Positives}

• Terugroepen (gevoeligheid of echt positief percentage): Herinneren meet het aandeel correct voorspelde positieve gevallen onder alle daadwerkelijke positieve gevallen.
  Recall = frac{ True , Positives}{True, Positives + False , Negatives}

• F1-score: F1-score is het harmonische gemiddelde van precisie en herinnering.
  F1 , Score = 2 * frac{Precision * Recall}{Precision + Recall}

• Gebied onder de bedrijfskarakteristiekcurve van de ontvanger (AUC-ROC): De ROC-curve zet het werkelijk positieve percentage uit tegen het fout-positieve percentage bij verschillende drempels. AUC-ROC meet het gebied onder deze curve en biedt een geaggregeerde maatstaf voor de prestaties van een model over verschillende classificatiedrempels heen.
• Gebied onder de Precision Recall-curve (AUC-PR): Vergelijkbaar met AUC-ROC, AUC-PR meet het gebied onder de curve voor precisie-herinnering en geeft een samenvatting van de prestaties van een model over verschillende afwegingen tussen precisie-herinnering.

Afweging tussen precisie en terugroepen bij het instellen van logistieke regressiedrempels

Logistieke regressie wordt pas een classificatietechniek als er een beslissingsdrempel in beeld wordt gebracht. Het instellen van de drempelwaarde is een zeer belangrijk aspect van logistieke regressie en is afhankelijk van het classificatieprobleem zelf.

De beslissing over de waarde van de drempelwaarde wordt in belangrijke mate beïnvloed door de waarden van precisie en herinnering. Idealiter willen we dat zowel precisie als herinnering 1 zijn, maar dit is zelden het geval.

In het geval van een Afweging tussen precisie en terugroepen , gebruiken we de volgende argumenten om de drempelwaarde te bepalen:

1. Lage precisie/hoge terugroepactie: In toepassingen waarbij we het aantal valse negatieven willen verminderen zonder noodzakelijkerwijs het aantal valse positieven te verminderen, kiezen we een beslissingswaarde met een lage waarde voor Precision of een hoge waarde voor Recall. Bij een toepassing voor de diagnose van kanker willen we bijvoorbeeld niet dat een getroffen patiënt als niet-aangedaan wordt geclassificeerd zonder er veel aandacht aan te besteden als bij de patiënt ten onrechte de diagnose kanker wordt gesteld. Dit komt omdat de afwezigheid van kanker kan worden gedetecteerd door andere medische ziekten, maar de aanwezigheid van de ziekte kan niet worden gedetecteerd bij een reeds afgewezen kandidaat.
2. Hoge precisie/lage terugroepactie: In toepassingen waarbij we het aantal valse positieven willen verminderen zonder noodzakelijkerwijs het aantal valse negatieven te verminderen, kiezen we een beslissingswaarde met een hoge waarde voor Precision of een lage waarde voor Recall. Als we bijvoorbeeld klanten classificeren of ze positief of negatief zullen reageren op een gepersonaliseerde advertentie, willen we er absoluut zeker van zijn dat de klant positief op de advertentie zal reageren, omdat een negatieve reactie anders een verlies aan potentiële omzet uit de advertentie kan veroorzaken. klant.

Verschillen tussen lineaire en logistieke regressie

Het verschil tussen lineaire regressie en logistische regressie is dat lineaire regressie-uitvoer de continue waarde is die van alles kan zijn, terwijl logistische regressie de waarschijnlijkheid voorspelt dat een instantie tot een bepaalde klasse behoort of niet.

csv-bestand lezen in Java

Logistieke regressie – Veelgestelde vragen (FAQ's)

Wat is logistieke regressie in machinaal leren?

Logistische regressie is een statistische methode voor het ontwikkelen van machine learning-modellen met binair afhankelijke variabelen, d.w.z. binair. Logistische regressie is een statistische techniek die wordt gebruikt om gegevens en de relatie tussen één afhankelijke variabele en één of meer onafhankelijke variabelen te beschrijven.

Wat zijn de drie soorten logistische regressie?

Logistieke regressie wordt ingedeeld in drie typen: binair, multinomiaal en ordinaal. Ze verschillen zowel in uitvoering als in theorie. Binaire regressie houdt zich bezig met twee mogelijke uitkomsten: ja of nee. Multinomiale logistische regressie wordt gebruikt als er drie of meer waarden zijn.

Waarom wordt logistische regressie gebruikt voor classificatieproblemen?

Logistieke regressie is gemakkelijker te implementeren, interpreteren en trainen. Het classificeert onbekende records zeer snel. Wanneer de dataset lineair scheidbaar is, presteert deze goed. Modelcoëfficiënten kunnen worden geïnterpreteerd als indicatoren voor het belang van een kenmerk.

Wat onderscheidt logistieke regressie van lineaire regressie?

Terwijl lineaire regressie wordt gebruikt om continue uitkomsten te voorspellen, wordt logistieke regressie gebruikt om de waarschijnlijkheid te voorspellen dat een waarneming in een specifieke categorie valt. Logistische regressie maakt gebruik van een S-vormige logistieke functie om voorspelde waarden tussen 0 en 1 in kaart te brengen.

Welke rol speelt de logistieke functie bij logistieke regressie?

Logistische regressie is afhankelijk van de logistieke functie om de uitvoer om te zetten in een waarschijnlijkheidsscore. Deze score vertegenwoordigt de waarschijnlijkheid dat een waarneming tot een bepaalde klasse behoort. De S-vormige curve helpt bij het drempelwaarden en categoriseren van gegevens in binaire uitkomsten.