Een encoder is een digitaal circuit dat een reeks binaire ingangen omzet in een unieke binaire code. De binaire code vertegenwoordigt de positie van de ingang en wordt gebruikt om de specifieke ingang te identificeren die actief is. Encoders worden vaak gebruikt in digitale systemen om een parallelle reeks ingangen om te zetten in een seriële code.
Het basisprincipe van een encoder is om aan elke mogelijke ingang een unieke binaire code toe te wijzen. Een encoder met 2 naar 4 lijnen heeft bijvoorbeeld 2 ingangslijnen en 4 uitgangslijnen en wijst een unieke 4-bits binaire code toe aan elk van de 2^2 = 4 mogelijke ingangscombinaties. De uitgang van een encoder is doorgaans actief laag, wat betekent dat er op elk moment slechts één uitgang actief (laag) is, en de overige uitgangen inactief (hoog). De actieve lage uitgang wordt geselecteerd op basis van de binaire code die aan de actieve ingang is toegewezen.
char naar Java met gehele getallen
Er zijn verschillende typen encoders, waaronder prioriteitsencoders, die aan elke ingang een prioriteit toekennen, en binair gewogen encoders, die een binair wegingssysteem gebruiken om binaire codes aan ingangen toe te wijzen. Samenvattend is een encoder een digitaal circuit dat een reeks binaire ingangen omzet in een unieke binaire code die de positie van de ingang vertegenwoordigt. Encoders worden veel gebruikt in digitale systemen om parallelle ingangen om te zetten in seriële codes.
Een encoder is een combinatorisch circuit dat de omgekeerde werking uitvoert van a Decoder . Het heeft een maximum van 2^n invoerregels En ‘n’ uitvoerregels , daarom codeert het de informatie van 2 ^ n-ingangen in een n-bit code. Het zal een binaire code produceren die equivalent is aan de invoer, die actief Hoog is. Daarom codeert de encoder 2^n invoerlijnen met ‘n’ bits.
Encoder
Soorten encoders
Er zijn verschillende soorten encoders die hieronder worden vermeld.
- 4 tot 2 Encoder
- Octale naar binaire encoder (8 tot 3 encoders)
- Decimaal naar BCD-encoder
- Prioriteitsencoder
4 tot 2 Encoder
De 4 tot 2 Encoder bestaat uit vier ingangen Y3, Y2, Y1 & Y0, en twee uitgangen A1 & A0 . Op elk moment kan slechts één van deze 4 ingangen ‘1’ zijn om de betreffende binaire code aan de uitgang te krijgen. De onderstaande afbeelding toont het logische symbool van de 4 naar 2-encoder.
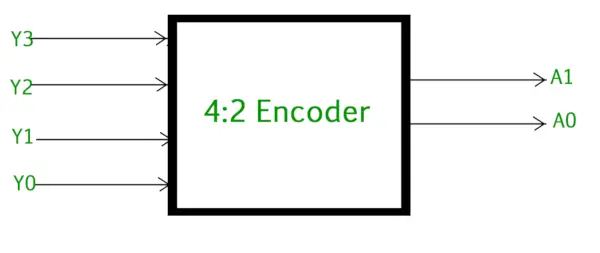
4 tot 2 Encoder
De waarheidstabel van 4 tot 2 encoders is als volgt.
| INGANGEN | UITGANGEN | ||||
|---|---|---|---|---|---|
| J3 | J2 | J1 | J0 | A1 | A0 |
| 0 | 0 | 0 | 1 | 0 | 0 |
| 0 | 0 | 1 | 0 | 0 | 1 |
| 0 | 1 | 0 | 0 | 1 | 0 |
| 1 | 0 | 0 | 0 | 1 | 1 |
Logische uitdrukking voor A1 en A0:
A1 = Y3 + Y2 A0 = Y3 + Y1>
De bovenstaande twee Booleaanse functies A1 en A0 kunnen worden geïmplementeerd met behulp van twee ingangs-OF-poorten:
converteer tekenreeks naar char java
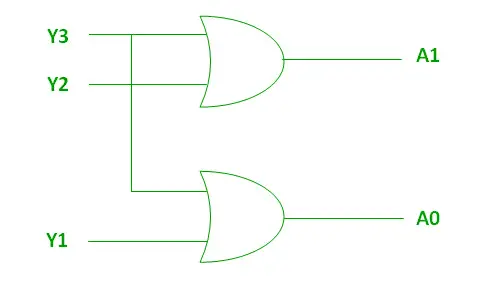
Implementatie met behulp van OR Gate
Octale naar binaire encoder (8 tot 3 encoders)
De 8 tot 3 Encoder of octaal naar binaire encoder bestaat uit 8 ingangen : Y7 tot Y0 en 3 uitgangen : A2, A1 & A0. Elke ingangslijn komt overeen met elk octaal cijfer en drie uitgangen genereren de overeenkomstige binaire code. De onderstaande afbeelding toont het logische symbool van octaal voor de binaire encoder.
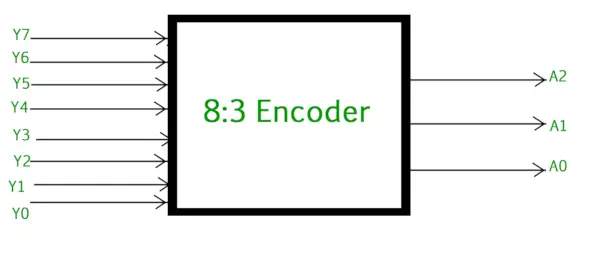
Octale naar binaire encoder (8 tot 3 encoders)
De waarheidstabel voor de 8 tot 3-encoder is als volgt.
| INGANGEN | UITGANGEN | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| J7 | J6 | J5 | J4 | J3 | J2 | J1 | J0 | A2 | A1 | A0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 |
| 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 |
| 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 1 |
| 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 |
| 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 |
| 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 |
Logische uitdrukking voor A2, A1 en A0.
A2 = Y7 + Y6 + Y5 + Y4 A1 = Y7 + Y6 + Y3 + Y2 A0 = Y7 + Y5 + Y3 + Y1>
De bovenstaande twee Booleaanse functies A2, A1 en A0 kunnen worden geïmplementeerd met behulp van vier invoer OF poorten .
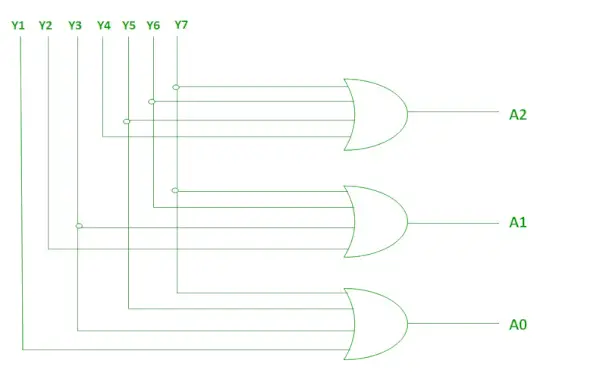
Implementatie met behulp van OR Gate
Decimaal naar BCD-encoder
De decimaal-naar-binaire encoder bestaat meestal uit 10 invoerlijnen En 4 uitvoerlijnen . Elke invoerregel komt overeen met elk decimaalcijfer en 4 uitgangen komen overeen met de BCD-code. Deze encoder accepteert de gedecodeerde decimale gegevens als invoer en codeert deze naar de BCD-uitvoer die beschikbaar is op de uitvoerlijnen. De onderstaande afbeelding toont het logische symbool van de decimaal naar BCD-encoder:
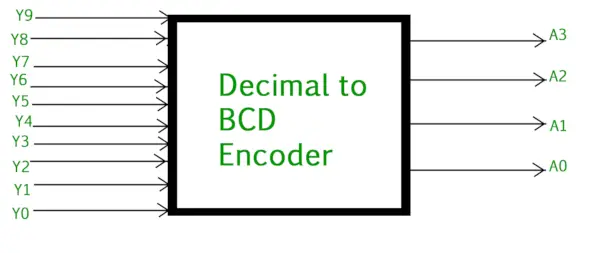
Decimaal naar BCD-encoder
De waarheidstabel voor decimalen naar BCD-encoder is als volgt.
csv-bestand java lezen
| INGANGEN | UITGANGEN | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Y9 | J8 | J7 | J6 | J5 | J4 | J3 | J2 | J1 | J0 | A3 | A2 | A1 | A0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 1 |
| 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 |
| 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 |
| 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 |
| 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 |
| 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 |
Logische uitdrukking voor A3, A2, A1 en A0.
A3 = Y9 + Y8 A2 = Y7 + Y6 + Y5 +Y4 A1 = Y7 + Y6 + Y3 +Y2 A0 = Y9 + Y7 +Y5 +Y3 + Y1>
De bovenstaande twee Booleaanse functies kunnen worden geïmplementeerd met behulp van OF-poorten.
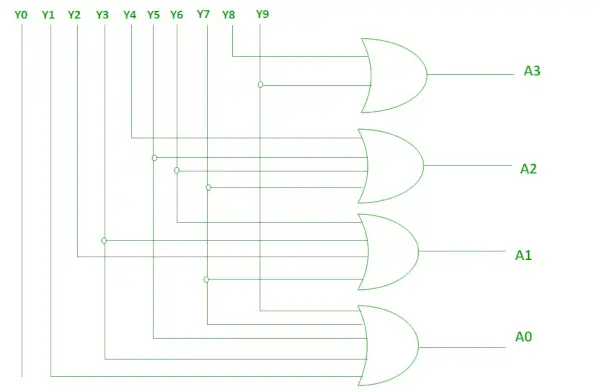
Implementatie met behulp van OR Gate
Prioriteitsencoder
Een encoder met 4 tot 2 prioriteit heeft 4 ingangen : Y3, Y2, Y1 & Y0, en 2 uitgangen : A1 & A0. Hier heeft de invoer Y3 de hoogste prioriteit , terwijl de invoer Y0 de laagste prioriteit . In dit geval zal, zelfs als meer dan één ingang tegelijkertijd ‘1’ is, de uitgang de (binaire) code zijn die overeenkomt met de ingang, die hogere prioriteit . De waarheidstabel voor de prioriteitsencoder is als volgt.
| INGANGEN | UITGANGEN | |||||
|---|---|---|---|---|---|---|
| J3 | J2 | J1 | J0 | A1 | A0 | IN |
| 0 | 0 | 0 | 0 | X | X | 0 |
| 0 | 0 | 0 | 1 | 0 | 0 | 1 |
| 0 | 0 | 1 | X | 0 | 1 | 1 |
| 0 | 1 | X | X | 1 | 0 | 1 |
| 1 | X | X | X | 1 | 1 | 1 |
De logische uitdrukking voor A1 wordt hieronder weergegeven.
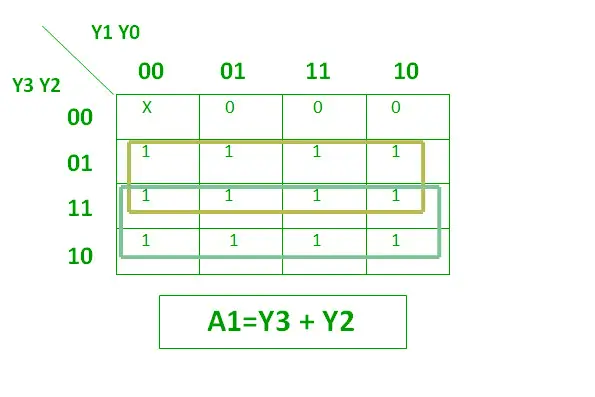
Logische expressie
grootte van vector c++
De logische expressie voor A0 wordt hieronder weergegeven.
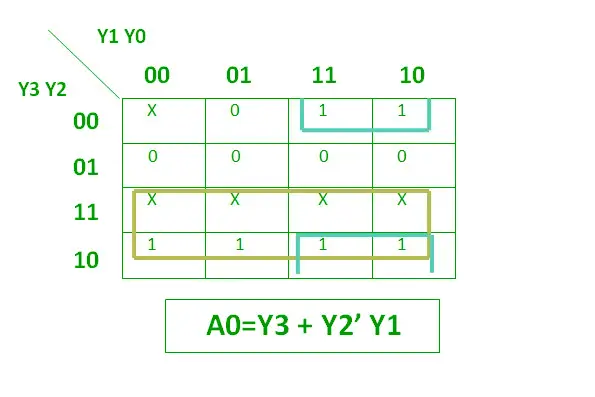
Logische expressie
De bovenstaande twee Booleaanse functies kunnen worden geïmplementeerd als.
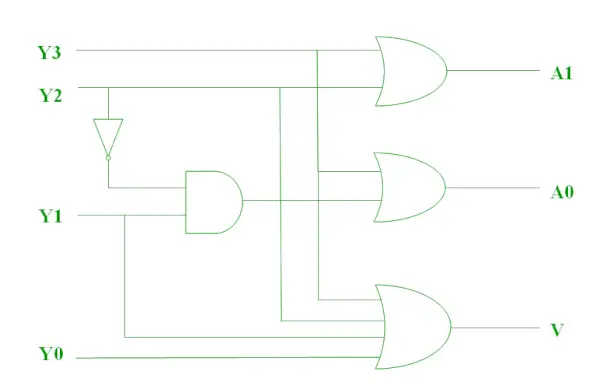
Prioriteitsencoder
Er zijn enkele fouten die meestal voorkomen in encoders. Deze worden hieronder vermeld.
- Er is sprake van dubbelzinnigheid wanneer alle uitgangen van de encoder gelijk zijn aan nul.
- Als er meer dan één ingang actief is Hoog, produceert de encoder een uitgang die mogelijk niet de juiste code is.
Om deze moeilijkheden te overwinnen, moeten we dus prioriteiten toekennen aan elke ingang van de encoder. Vervolgens zal de uitgang van de encoder de code zijn die overeenkomt met de actieve hoge ingangen, die een hogere prioriteit hebben.
Toepassing van encoders
- Encoders zijn veel voorkomende elektronische circuits die in alle digitale systemen worden gebruikt.
- Encoders worden gebruikt om de decimale waarden naar het binaire getal te vertalen om binaire functies uit te voeren, zoals optellen, aftrekken, vermenigvuldigen, enz.
- Andere toepassingen, vooral voor Priority Encoders, kunnen het detecteren van interrupts in microprocessortoepassingen omvatten.
Voordelen van het gebruik van encoders in digitale logica
- Vermindering van het aantal regels: Encoders verminderen het aantal lijnen dat nodig is om informatie van meerdere ingangen naar één uitgang te verzenden, wat het ontwerp van het systeem kan vereenvoudigen en de kosten van componenten kan verlagen.
- Verbeterde betrouwbaarheid: Door meerdere ingangen om te zetten in één seriële code kunnen encoders de kans op fouten bij de overdracht van informatie verkleinen.
- Verbeterde prestatie: Encoders kunnen de prestaties van een digitaal systeem verbeteren door de hoeveelheid tijd te verminderen die nodig is om informatie van meerdere ingangen naar één uitgang te verzenden.
Nadelen van het gebruik van encoders in digitale logica
- Verhoogde complexiteit: Encoders zijn doorgaans complexere circuits vergeleken met multiplexers , en er zijn extra componenten nodig om te implementeren.
- Beperkt tot specifieke toepassingen: Encoders zijn alleen geschikt voor toepassingen waarbij een parallelle set ingangen moet worden omgezet in een seriële code.
- Beperkte flexibiliteit: Encoders zijn beperkt in hun flexibiliteit, omdat ze slechts een vast aantal ingangen kunnen coderen in een vast aantal uitgangen.
- Kortom, encoders zijn nuttige digitale circuits die hun voor- en nadelen hebben. De keuze om al dan niet een encoder te gebruiken hangt af van de specifieke vereisten van het systeem en de afweging tussen complexiteit, betrouwbaarheid, prestaties en kosten.
GATE CS Hoekvragen
Door de volgende vragen te oefenen, kunt u uw kennis testen. Alle vragen zijn de afgelopen jaren in GATE gesteld of in GATE Mock Tests. Het wordt ten zeerste aanbevolen om ze te oefenen.
- GATE CS 2013, vraag 65
- GATE CS 2014 (set 3), vraag 65
