Een cirkel bestaat uit punten die allemaal op dezelfde afstand van het middelpunt van de cirkel liggen. Een gesloten geometrische vorm is een cirkel. In het dagelijks leven zien we cirkels in de vorm van een wiel, pizza's, een ronde ondergrond, enzovoort.

Delen van een cirkel

Sara Ali Khan leeftijd

Belangrijkste termen:

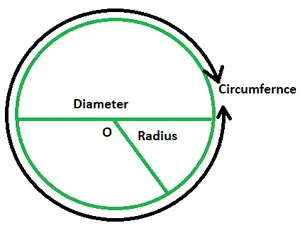
• Straal: De straal van een cirkel is de afstand tussen het middelpunt en een willekeurig punt op de rand. Het wordt algemeen aangeduid als r. Een cirkel heeft een oneindig aantal stralen.
• Diameter: Het is een lijn die door het midden loopt en zijn uiteinden op de cirkel heeft. Het wordt aangegeven als D en is tweemaal de waarde van de straal van de cirkel.
• Omtrek: De omvang van de rand van de cirkel is gelijk aan de omtrek. Dit betekent dat de omtrek van een cirkel gelijk is aan de omtrek ervan. De omtrek van de cirkel is gelijk aan de lengte van de draad die zich netjes om de omtrek wikkelt. Het wordt gegeven als 2πr.

Wat is het gebied van de cirkel?

De oppervlakte van een cirkel heeft betrekking op de hoeveelheid ruimte die de rand van een cirkel omsluit. Het gebied dat door de cirkel wordt gevuld, is het gebied binnen de omtrek van de cirkel. Het wordt ook wel het totale aantal vierkante eenheden in de cirkel genoemd.

Rekening: Diameter van een cirkel

Gebied van cirkelformules

De oppervlakte van een cirkel wordt gegeven door de volgende formule:

A = πr ²

waarbij r de straal van de gegeven cirkel is.

of

EEN = C ² /4p

waarbij C de omtrek van de gegeven cirkel is.

Voorbeelden waarbij de formule voor het gebied van de cirkel wordt gebruikt

Vraag 1. Vind de oppervlakte van een cirkel, gegeven dat de straal 8 m is.

wat is uri

Oplossing:

Gegeven: r = 8 m

Omdat de oppervlakte van een cirkel = πr²

EEN = π(8)²

= 64p

= 200,96 m ²

Vraag 2. Bereken de oppervlakte van een cirkel, gegeven dat de omtrek 12 cm is.

Oplossing:

Gegeven: C = 12 cm

Aangezien A = C²/4p

= 12²/4p

= 11,46 cm ²

Vraag 3. Bereken de oppervlakte van een cirkel, gegeven dat de diameter 12 cm is.

Oplossing:

Gegeven: D = 12 cm

of, Straal = r = 12/2 = 6 cm

Aangezien A = πr²

= π(6)2

= 113,04 cm ²

Vraag 4. Bereken de oppervlakte van een cirkel, gegeven dat de straal 9 cm is.

lengte van tekenreeks-java

Oplossing:

Gegeven: r = 9 m

Omdat de oppervlakte van een cirkel = πr²

EEN = π(9)²

= 81p

concat-tekenreeksen java

= 254,34 cm ²

Vraag 5. Bereken de oppervlakte van een cirkel, gegeven dat de diameter 10 cm is.

Oplossing:

Gegeven: D = 10 cm

of, Straal = r = 10/2 = 5 cm

Aangezien A = πr²

= π(5)²

= 78,5 cm ²

Controleer ook:

• Gebied Van Een Cirkelcalculator
• Vierkante beelden van cirkelcalculator
• Straal van een cirkelcalculator
• Diameter Van Een Cirkelcalculator
• Omtrekcalculator
• Berekening van omtrek naar diameter