De vierkantswortel van 3 is een positief reëel getal dat het getal 3 oplevert als het met zichzelf wordt vermenigvuldigd. De vierkantswortel van 3 is een irrationeel getal, omdat het een niet-afsluitend en niet-herhalend decimaal getal is. Vierkantswortel van 3 wordt aangegeven als √3 of 31/2. Omdat het kwadraat van 3 een irrationeel getal is, wordt de exacte decimale waarde nooit berekend.
Waarde van de vierkantswortel van 3, √3 =1,732 (afgeknot)
In dit artikel zullen we in detail leren over de vierkantswortel van 3.
f films
Inhoudsopgave
- Wat is vierkantswortel van 3?
- Root 3-waarde in wiskunde
- Is de vierkantswortel van 3 rationeel of irrationeel?
- Hoe vind je de vierkantswortel van 3?
- Eigenschappen van de vierkantswortel van een getal
- Tabel met vierkantswortel
Wat is vierkantswortel van 3?
De vierkantswortel van een getal is een getal dat, wanneer het met zichzelf wordt vermenigvuldigd, resulteert in het oorspronkelijke getal.
Voorbeeld: Vierkantswortel van 16 is 4, aangezien 4×4 = 16 dus √16 = 4
Vierkantswortel van 3 of eenvoudigweg wortel 3 genoemd, is een irrationeel getal dat door vermenigvuldiging met zichzelf resulteert in het getal 3. We kunnen de geschatte waarde van wortel 3 geven als:
- Decimale vorm: 1,732
- Exponentvorm: 31/2
- Radicaalvorm: √3
Root 3-waarde in wiskunde
In de wiskunde is het vinden van de vierkantswortel van elk getal erg belangrijk; de vierkantswortel van het perfecte vierkant kan eenvoudig worden berekend. Voor onvolmaakte vierkanten is het vinden van een vierkantswortel moeilijk en deze wordt over het algemeen berekend met behulp van de staartdelingsmethode.
De wortel van 3 wordt uitgedrukt als √3. Het is een irrationeel getal, dus de decimale waarde ervan kan nooit worden berekend. Het wordt in de radicale vorm weergegeven als (3)½. De wortel van 3, afgerond op 7 decimalen, is 1,7320508.
Vierkantswortel van 3 = 1,7320508075688772…
Is de vierkantswortel van 3 rationeel of irrationeel?
Vierkantswortel 3 is een niet-afsluitend en niet-herhalend decimaalteken en alle niet-afsluitende en niet-herhalende decimalen vallen onder irrationeel getal. Het is dus veilig om te zeggen dat √3 an is irrationeel nummer .
toetsenbord voor pagina omlaag
Decimale uitbreiding van de vierkantswortel van 3 is,
√3 = 1,7320508075688772…
Omdat het zich niet herhaalt en niet eindigt, kunnen we zeker zeggen dat √3 irrationeel is.
Hoe vind je de vierkantswortel van 3?
Het is altijd gemakkelijker om de vierkantswortel van perfecte vierkanten te berekenen, maar om de vierkantswortel van een niet-perfect vierkant te berekenen, moeten we de staartdelingmethode gebruiken.
Om de vierkantswortel van 3 te berekenen, moeten we de onderstaande stappen volgen:
Stap 1: Schrijf 3 als 3,000000 (waarbij nullen altijd in de vorm van paren worden bewaard) om het delen gemakkelijker te maken.
Stap 2: Zoek nu naar het perfecte vierkant kleiner dan 3, d.w.z. 1, en deel het getal daarmee.
Stap 3: Nu is het quotiënt 1 en de rest is 2. We plaatsen een decimaal in het quotiënt en brengen het paar nullen naar beneden voor verdere deling.
Stap 4: Nu is het volgende deeltal 200. Voeg toe dat de volgende deler 2X is (quotiënt 1 wordt opgeteld bij de vorige deler 1 en X staat op de tiende plaats), zodat de vermenigvuldiging van het getal 2X en X kleiner moet zijn dan 200. Dit geeft de volgende waarde 27 als de nieuwe deler.
Stap 5: Nu wordt 7 achter de komma opgeteld bij het quotiënt, dus de waarde van het quotiënt wordt 1,7 en de nieuwe deler wordt verkregen door 7 bij 27 op te tellen, dus 34Y, waarbij Y op de honderdste plaats staat. Met behulp van de voorgaande stappen kunnen we doorgaan en verkrijgen we de vierkantswortel van 3 in het quotiënt.
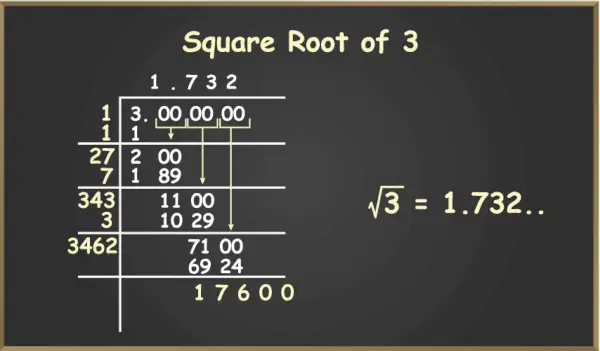
Vierkantswortel van 3
Breng nu het volgende paar nullen naar beneden en herhaal stap 4 en 5. Dit kan voor oneindige stappen worden gedaan, aangezien de exacte waarde van de vierkantswortel van 2 tot in het oneindige aantal decimalen reikt. We kunnen het resultaat berekenen tot op 4 cijfers achter de komma, aangezien dit kan worden gebruikt voor ca. waarde van de vierkantswortel.
Eigenschappen van de vierkantswortel van een getal
Hieronder worden verschillende eigenschappen van de vierkantswortel van een getal besproken,
- Perfecte vierkante getallen hebben perfecte vierkantswortels.
- De vierkantswortel van een even perfect vierkant is even.
- De wortel van een oneven perfect vierkant is oneven.
- De vierkantswortel van een negatief getal is a complex getal .
Tabel met vierkantswortel
Vierkantswortels van verschillende getallen worden veel gebruikt in de wiskunde. De onderstaande tabel geeft ons de vierkantswortel van verschillende getallen die vaak worden gebruikt.
| Nummer | Vierkantswortel |
|---|---|
| 1 | √(1) = 1 |
| 2 | √(2) = 1,414 (ongeveer) |
| 3 | √(3) = 1,732 (ongeveer) |
| 4 | √(4) = 2 |
| 5 | √(5) = 2,236(ongeveer) |
| 9 | √(9) = 3 |
| 16 | √(16) = 4 |
| 25 | √(25) = 5 |
Controleer ook
- Vierkantswortel van 2
- Echte getallen
- Rationele nummers
Veelgestelde vragen over vierkantswortel van 3
Wat is de waarde van de vierkantswortel van 3?
De geschatte waarde van de vierkantswortel van 3 is 1,73205.
Waarom is de vierkantswortel van 3 een irrationeel getal?
De waarde van de vierkantswortel van 3 is een niet-herhalend en niet-afsluitend decimaal getal, dus het is een irrationeel getal.
vijandige zoektocht
Is het getal 3 een perfect vierkant?
3 is een priemgetal en priemgetallen hebben geen andere factoren dan 1 en zichzelf. We kunnen dus zeggen dat 3 geen perfect vierkant is.
Hoe kunnen we de waarde van √3 vinden?
De waarde van √3 kan worden gevonden met behulp van de staartdelingsmethode. Omdat 3 geen perfect vierkant is, wordt de exacte waarde ervan nooit gevonden.
Wat is de waarde van wortel 2?
Wortel 2 is een irrationeel getal, dus de exacte decimale waarde ervan wordt nooit gevonden. Geschatte waarde van wortel 2 is, √2 = 1,414 (ongeveer)
