- Bitwise XOR-operator is ook bekend als Exclusief of
- Het wordt aangegeven met behulp van de '^'
- Zoals de naam aangeeft, werkt het op de beetje niveau van de operanden.
- Bitwise XOR-operator valt onder de categorie Bitwise-operators.
- In de bitsgewijze exclusieve OR-operator (XOR) zijn twee operanden vereist, en deze twee operanden worden gescheiden door het XOR-symbool, dat wil zeggen '^'.
- Om de uitvoer of het resultaat te bepalen dat eruit komt na het toepassen van de XOR-operator op twee operanden, moeten we de logische waarheidstabel van de XOR-operator volgen.
- XOR Truth Table is de wiskundige tabel die is opgebouwd met behulp van de juiste logica van de XOR-operator.
- De logica die achter de XOR-operator wordt gebruikt is; wanneer XOR-bewerking op de twee wordt toegepast verschillend bits van twee operanden, dan zal het resultaat altijd opleveren '1', en of de XOR-bewerking op de twee wordt toegepast dezelfde bits van twee operanden, waarna het resultaat uitvoer oplevert '0'.
Waarheidstabel van exclusieve OR (XOR)-operator
Stel dat er twee operanden zijn; de eerste is A en de tweede is B, het totale aantal invoercombinaties gevormd door deze twee operanden zal 4 zijn. Door de volgende XOR-waarheidstabel te gebruiken, zullen we de overeenkomstige uitvoer bepalen. Het resultaat wordt hier in C vastgelegd C = EEN ^ B.
In deze waarheidstabel nemen we invoer in de vorm van bits, dat wil zeggen 0 en 1, en de uitvoer wordt ook gegenereerd in de vorm van bits, dat wil zeggen 0 en 1.
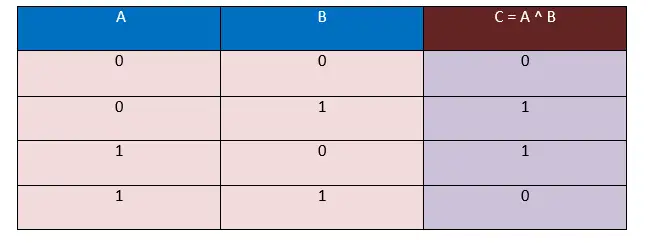
Hier, in de bovenstaande XOR Truth-tabel, zien we dat wanneer de waarden van operanden A en B verschillend zijn, d.w.z. ( 0, 1 ), ( 1, 0 ), het resultaat dat uitkomt altijd 1 zal zijn. En wanneer de waarden van operanden A en B zijn hetzelfde, d.w.z. ( 0, 0 ), ( 1, 1 ), het resultaat dat eruit komt zal altijd 0 zijn.
Op dezelfde manier kunnen we op deze manier de waarheidstabel tekenen Booleaans waarden -
pd.merge
Stel dat er twee operanden zijn; de eerste is A en de tweede is B . Het totale aantal invoercombinaties gevormd door deze twee operanden zal 4 zijn. Door de volgende XOR-waarheidstabel te gebruiken, zullen we de overeenkomstige uitvoer bepalen. Het resultaat wordt vastgelegd in C, hier C = A ^ B.
In deze waarheidstabel nemen we input in de vorm van Waarheidswaarden, dat wil zeggen Waar (T) en Onwaar (F). De uitvoer wordt ook gegenereerd in de vorm van True-waarden, d.w.z. T en F.

Hier, in de bovenstaande XOR Truth-tabel, zien we dat, wanneer de waarden van operanden A en B verschillend zijn, dat wil zeggen (F, T), (T, F), het resultaat altijd T zal zijn. En wanneer de waarden van operanden A en B zijn hetzelfde, d.w.z. ( F, F ), ( T, T ), het resultaat zal altijd F zijn.
Uit de bovenstaande tabellen zien we dat T (True) wordt aangegeven met één en F (False) wordt aangegeven met 0.
Stappen om een bepaald probleem op te lossen -
- De operanden die in de opgave worden gegeven, hebben altijd een decimale waarde.
- Ten eerste moeten we de waarden van operanden omzetten in binair
- Nadat u de waarden van operanden in binaire getallen hebt omgezet, plaatst u beide operanden boven elkaar.
- Houd er rekening mee dat u, voordat u de exclusieve OR (XOR)-bewerking erop toepast, eerst de aantal getallen in hen.
- Als het aantal cijfers niet overeenkomt, brengen de extra nullen aan de linkerkant van de kleine operand het aantal cijfers in evenwicht.
- Tenslotte, met behulp van de bovenstaande waarheidstabel, past u de XOR-bewerking één voor één toe op de operanden, waarbij u bit voor bit neemt voor het toepassen van de XOR-bewerking.
- Uiteindelijk wordt het resultaat geproduceerd in de vorm van output.
- De uitvoer die wordt geproduceerd, is in binaire vorm. Converteer nu de binaire vorm naar decimale vorm en noteer de resultaatwaarde.
Uitvoering van Bitwise Exclusive OR (XOR)-bewerking in C++
Laten we meer in detail begrijpen over de uitvoering van de XOR-bewerking in C++ met behulp van voorbeelden -
Voorbeeld 1: Vind de exclusieve OR van gehele waarden; 10 en 14. Leg het ook uit en schrijf de uitvoeringscode in C++.
Oplossing: Laten we twee variabelen bekijken, 'a' en 'b', om de corresponderende twee operanden op te slaan die in de bovenstaande vraag zijn gegeven, namelijk 10 en 14.
in tekenreeks in Java
Hier geldt a = 10 en b = 14.
We zullen de onderstaande stappen volgen om de exclusieve OR van de gegeven twee operanden te achterhalen.
- We weten dat 10 en 14 in decimale vorm zijn, en voor het toepassen van bitsgewijze XOR-bewerking is het noodzakelijk om deze naar binaire vorm te converteren.
- Binaire vorm 'a', d.w.z. 10 is '1010' en binaire vorm van 'b', d.w.z. 14 is '1110'.
- Hier zien we dat het aantal binaire cijfers in a vier is en dat het aantal binaire cijfers in b ook 4 is; Daarom is het aantal binaire cijfers in beide variabelen hetzelfde en al in evenwicht. We hoeven niet meer nullen toe te voegen om het in evenwicht te brengen.
- Nu moeten we de binaire cijfers in 'b' terugbrengen tot de binaire cijfers in 'a'.
- Tenslotte past het één voor één toepassen van de XOR-bewerking op de overeenkomstige bits toe en noteert u de uitvoer.
- De uiteindelijk gegenereerde uitvoer zal in binaire vorm zijn, zoals de bovenstaande vraag in decimale vorm heeft gegeven, dus we moeten het resultaat in decimale vorm converteren.
Uitleg:
a = 10 (in decimale vorm)
b = 14 (in decimale vorm)
Voor een XOR b moeten we nu a en b in binaire vorm converteren -
a = 1010 (in binaire vorm)
b = 1110 (in binaire vorm)
Nu XOR-bewerking toepassen op a en b -
a = 1010
uitzonderingsafhandeling in Java
b = 1110
---------------
a ^ b = 0100 (In binaire vorm)
Het resultaat van a ^ b is 0100, wat in binaire vorm is.
Converteer nu het resultaat in decimale vorm, namelijk 4.
10^14 = 4
OPMERKING: Door de bovenstaande XOR-waarheidstabel te gebruiken, wordt de uitvoer van overeenkomstige bits gegenereerd.
We zullen nu de bitsgewijze XOR-bewerking toepassen op 10 en 14 in de C++-taal en het resultaat krijgen, d.w.z. 4.
C++ code voor bovenstaand voorbeeld:
//************************ C++ Code ****************************** #include using namespace std; int main () { int a, b, c ; // Initializing integer variables to store data values cout <' << endl ; cout <> a ; // taking a as input from user cout <> b ; // taking b as input from user c = a ^ b ; // storing XOR result of a and b in c cout << 'Applying XOR operation on a and b: '<< endl ; cout << 'a ^ b = ' << c << endl ; // Printing the output } </'> Uitvoer

Voorbeeld 2: Vind de exclusieve OR van gehele waarden; 3 en 15. Leg het ook uit en schrijf de uitvoeringscode in C++.
Oplossing: Laten we twee variabelen bekijken, 'a' en 'b', om de corresponderende twee operanden op te slaan die in de bovenstaande vraag zijn gegeven, namelijk 3 en 15.
Hier geldt a = 3 en b = 15.
We zullen de onderstaande stappen volgen om de exclusieve OR van de gegeven twee operanden te achterhalen.
- We weten dat 3 en 15 in decimale vorm zijn, en voor het toepassen van bitsgewijze XOR-bewerking is het noodzakelijk om deze naar binaire vorm te converteren.
- Binaire vorm 'a', d.w.z. 3 is 'elf' en binaire vorm van 'b', d.w.z. 15 is '1111'.
- Hier zullen we zien dat het aantal binaire cijfers in a twee is en het aantal binaire cijfers in b vier; daarom is het aantal binaire cijfers in beide variabelen niet hetzelfde. Als we dus uit balans zijn, moeten we meer nullen toevoegen aan de linkerkant van het lagere binaire getal, d.w.z. a, wat ' elf' , om het in evenwicht te brengen.
- Na het balanceren is de waarde van a gelijk '0011' , en b is '1111'.
- Nu moeten we de binaire cijfers in 'b' terugbrengen tot de binaire cijfers in 'a'.
- Tenslotte past het één voor één toepassen van de XOR-bewerking op de overeenkomstige bits toe en noteert u de uitvoer.
- De uiteindelijk gegenereerde uitvoer zal in binaire vorm zijn, zoals de bovenstaande vraag in decimale vorm heeft gegeven, dus we moeten het resultaat in decimale vorm converteren.
Uitleg:
a = 3 (in decimale vorm)
b = 15 (in decimale vorm)
Voor een XOR b moeten we nu a en b in binaire vorm converteren -
java int in tekenreeks
a = 0011 (in binaire vorm)
b = 1111 (in binaire vorm)
Nu XOR-bewerking toepassen op a en b -
a = 0011
b = 1111
---------------
a ^ b = 1100 (In binaire vorm)
Het resultaat van a ^ b is 1100, wat in binaire vorm is.
java willekeurige wiskunde willekeurig
Converteer nu het resultaat in decimale vorm, namelijk 12.
3^15 = 12
OPMERKING: Door de bovenstaande XOR-waarheidstabel te gebruiken, wordt de uitvoer van overeenkomstige bits gegenereerd.
We zullen nu de bitsgewijze XOR-bewerking toepassen op 3 en 15 in de C++-taal en het resultaat krijgen, d.w.z. 12.
C++ code voor bovenstaand voorbeeld:
//************************ C++ Code ****************************** #include using namespace std; int main () { int a, b, c ; // Initializing integer variables to store data values cout <' << endl ; cout <> a ; // taking a as input from user cout <> b ; // taking b as input from user c = a ^ b ; // storing XOR result of a and b in c cout << 'Applying XOR operation on a and b: '<< endl ; cout << 'a ^ b = ' << c << endl ; // Printing the output } </'> Uitvoer

