Veelhoek in wiskunde is een tweedimensionale vorm die bestaat uit rechte lijnen die een gesloten veelhoekige keten vormen. Het woord polygoon komt van de woorden poly en gon, wat veel en zijden betekent.
Veelhoeken kunnen eenvoudig zijn of zichzelf snijden. Een eenvoudige polygoon snijdt zichzelf niet, behalve op de gedeelde eindpunten van opeenvolgende segmenten. Een veelhoekige keten die zichzelf kruist, creëert een zichzelf snijdende veelhoek. Veelhoeken kunnen ook worden geclassificeerd als concaaf of convex.
In dit artikel hebben we uitgebreid gesproken over polygonen en hun typen, formules en voorbeelden.
| Belangrijke feiten over veelhoeken volledige opteller | |
|---|---|
| Som van binnenhoeken van veelhoek | (n–2) × 180° |
| Aantal diagonalen in veelhoek | n(n–3)/2 |
| Binnenhoek van regelmatige veelhoek | {(n–2) × 180°}/n |
| Buitenhoek van regelmatige veelhoek | 360°/n |
Inhoudsopgave
- Wat zijn veelhoeken?
- Veelhoekdiagram op basis van het aantal zijden
- Eigenschappen van veelhoeken
- Veelhoekvormen
- Soorten veelhoeken
- Veelhoekformules
- Hoeken in veelhoeken
- Veelgestelde vragen
Wat zijn veelhoeken?
De term 'Polygoon' komt van het Griekse woord polugonos, waarbij 'poly' 'veel' betekent, en 'gon' 'hoek'. Over het algemeen is een polygoon een gesloten figuur gevormd door rechte lijnen, waarvan de binnenhoeken daardoor worden gecreëerd lijnen. Om een gesloten vorm te vormen zijn minimaal drie lijnsegmenten nodig. Het is algemeen bekend als een driehoek of een driehoek. De algemene term voor een n-zijdige veelhoek is een n-hoek.
Veelhoekdefinitie
Veelhoeken zijn platte, tweedimensionale figuren bestaande uit rechte zijden die een volledig omsloten vorm vormen. In de meetkunde is de veelhoek een vlakke figuur die bestaat uit lijnsegmenten die met elkaar zijn verbonden om een gesloten veelhoekige keten te vormen. Ze bestaan uit rechte zijden, geen rondingen, en kunnen een variërend aantal zijden hebben. Sommige polygonen van verschillende soorten zijn: open, alleen grens, gesloten en zichzelf kruisend.
In de meetkunde wordt een veelhoek gedefinieerd als een gesloten, tweedimensionale vorm die plat in een vlak ligt en wordt omsloten door rechte zijden.
Een veelhoek heeft geen gebogen zijden en de randen zijn de rechte segmenten die de grens bepalen. De ontmoetingspunten van deze randen worden hoekpunten of hoeken genoemd.
Veelhoek voorbeelden
In termen van wiskunde zijn driehoeken, zeshoeken, vijfhoeken en vierhoeken voorbeelden van veelhoeken. Voorbeelden uit de praktijk van Polygon zijn het rechthoekige scherm op uw laptop, televisie, mobiele telefoon; rechthoekig voetbalveld of speeltuin, de Bermudadriehoek en de driehoekige piramides van Egypte.

Delen van een veelhoek
Een veelhoek bestaat uit drie fundamentele componenten:
- Zijden van veelhoek: Zijden van polygonen zijn de grenzen van de polygonen die het gesloten gebied definiëren.
- Hoekpunten: Het punt waarop twee zijden elkaar ontmoeten, staat bekend als een hoekpunt.
- Hoeken: De veelhoek bevat zowel binnen- als buitenhoeken. Er wordt een binnenhoek gevormd binnen het omsloten gebied van de veelhoek door het snijpunt van de zijkanten ervan.
Veelhoekdiagram op basis van het aantal zijden
Nomenclatuur van veelhoek gedefinieerd op basis van het aantal zijden dat ze bezitten. Het wordt aangeduid als n-gonen, waarbij ‘n’ het aantal zijden betekent. Veelhoeken worden over het algemeen geïdentificeerd aan de hand van de hoeveelheid randen. Een veelhoek met vijf zijden wordt bijvoorbeeld een 5-hoek genoemd, terwijl een veelhoek met tien zijden een 10-hoek wordt genoemd.
| Veelhoekdiagram | ||||
|---|---|---|---|---|
| Namen van veelhoekvormen | Aantal zijden | Aantal hoekpunten | Aantal diagonalen | Binnenhoekmaat voor normale vorm |
| Driehoek | Veelhoeken met 3 zijden | 3 | 0 | 60° |
| Vierhoek | Veelhoeken met 4 zijden | 4 | 2 | 90° |
| Pentagon | Veelhoeken met 5 zijden | 5 | 5 | 108° |
| Zeshoek | Veelhoeken met 6 zijden | 6 | 9 | 120° |
| Zevenhoek | Veelhoeken met 7 zijden | 7 | 14 | 128,571° |
| Achthoek | Veelhoeken met 8 zijden | 8 | twintig | 135° |
| Nonagon | Veelhoeken met 9 zijden | 9 | 27 | 140° |
| Tienhoek | Veelhoeken met 10 zijden | 10 | 35 | 144° |
| Hendecagon | Veelhoeken met 11 zijden | elf | 44 | 147,273° |
| Dodecagon | Veelhoeken met 12 zijden | 12 | 54 | 150° |
Eigenschappen van veelhoeken
De eigenschappen van polygonen identificeren ze gemakkelijk. De volgende eigenschappen dragen ertoe bij dat u de polygonen gemakkelijk leert kennen:
- Een polygoon is een gesloten vorm, zonder open uiteinden. Oorsprong en eindpunt moeten hetzelfde zijn.
- Het neemt een vlakke vorm aan, bestaande uit lijnsegmenten of rechte lijnen die samen de figuur vormen.
- Als tweedimensionale entiteit bestaat een polygoon alleen in de afmetingen lengte en breedte, zonder diepte of hoogte.
- Het bezit drie of meer zijden om een veelhoek te maken.
- Hoeken in de veelhoek kunnen variëren. Het toont een aparte configuratie.
- De lengte van de zijden van een polygoon kan variëren; het kan wel of niet gelijk zijn over de veelhoek.
Veelhoekvormen
Een polygoon is een platte, tweedimensionale vorm die wordt gekenmerkt door rechte zijden die met elkaar zijn verbonden om een gesloten figuur te vormen. Voorbeelden van polygoonvormen zijn onder meer:
- Driehoek
- Vierhoek
- Pentagon
- Zeshoek
- Zevenhoek
- Achthoek
- Nonagon
- Tienhoek
Driehoek
- Het heeft 3 zijden en 3 hoekpunten.
- Het heeft geen diagonalen.
- De som van het interieur is 180°.
Vierhoek
- Het heeft 4 zijden en 4 hoekpunten.
- Het heeft 2 diagonalen.
- De som van de binnenhoek is 360°.
Pentagon
- Het heeft 5 zijden en 5 hoekpunten.
- Het heeft 5 diagonalen.
- De som van de binnenhoek is 540°.
Zeshoek
- Het heeft 6 zijden en 6 hoekpunten.
- Het heeft 9 diagonalen.
- De som van de binnenhoek is 720°.
Zevenhoek
- Het heeft 7 zijden en 7 hoekpunten.
- Het heeft 14 diagonalen.
- De som van de binnenhoek is 900°.
Achthoek
- Het heeft 8 zijden en 8 hoekpunten.
- Het heeft 20 diagonalen.
- De som van de binnenhoek is 1080°.
Nonagon
- Het heeft 9 zijden en 9 hoekpunten.
- Het heeft 27 diagonalen.
- De som van de binnenhoek is 1260°.
Tienhoek
- Het heeft 10 zijden en 10 hoekpunten.
- Het heeft 35 diagonalen.
- De som van de binnenhoek is 1440°.
Soorten veelhoeken
Afhankelijk van de zijkanten en hoeken kunnen de polygonen op verschillende basis in verschillende typen worden ingedeeld, zoals:
- Op basis van zijden
- Op basis van hoeken
- Op basis van grens
Veelhoeken op basis van zijden
Veelhoeken kunnen op basis van de kenmerken van hun zijden worden onderverdeeld in twee primaire typen:
- Regelmatige veelhoek
- Onregelmatige veelhoek
Regelmatige veelhoek
Een regelmatige veelhoek onderscheidt zich doordat alle zijden even lang zijn en alle binnenhoeken even groot zijn. Het kan zowel gelijkzijdig als gelijkhoekig zijn. Voorbeelden van regelmatige veelhoeken zijn de driehoek, vierhoek, vijfhoek en zeshoek.

Regelmatige veelhoek
Onregelmatige veelhoek
Een onregelmatige veelhoek heeft zijden en hoeken van ongelijke lengte met verschillende afmetingen. Elke polygoon die niet voldoet aan de criteria van een regelmatige polygoon wordt geclassificeerd als onregelmatig. Veel voorkomende voorbeelden van onregelmatige veelhoeken zijn de ongelijkzijdige driehoek, vierhoeken zoals rechthoek, trapezium of vlieger, evenals onregelmatige vijfhoekige en zeshoekige structuren.
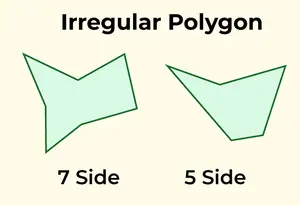
Onregelmatige veelhoek
Veelhoeken op basis van hoeken
Veelhoeken kunnen op basis van de aard van hun hoeken worden ingedeeld in twee hoofdcategorieën:
- Convexe veelhoek
- Concave veelhoek
Convexe veelhoek
Een convexe veelhoek heeft geen binnenhoek die groter is dan 180°. Convexe polygonen kunnen drie of meer zijden hebben. Bij convexe veelhoeken liggen alle diagonalen binnen de gesloten figuur. Veel voorkomende voorbeelden van convexe veelhoeken zijn driehoeken, allemaal convexe vierhoeken, evenals regelmatige vijfhoeken en zeshoeken
Concave veelhoek
Een concave veelhoek heeft ten minste één binnenhoek die een reflexhoek is en naar binnen wijst. Holle polygonen hebben minimaal vier zijden. Dit type polygoon heeft ten minste één binnenhoek van meer dan 180°. In concave veelhoeken strekken sommige diagonalen zich uit buiten de bijgevoegde figuur. Voorbeelden van concave veelhoeken zijn onder meer een pijlpunt of een pijlpunt in vierhoeken, evenals bepaalde onregelmatige vijfhoeken en zeshoeken.
Verschil tussen concave en convexe polygonen
Laten we het verschil tussen Convexe en Concave Polygoon in de onderstaande tabel bekijken:

| Convexe veelhoek | Concave veelhoek |
|---|---|
| De gehele omtrek van een convexe vorm strekt zich naar buiten uit zonder enige inkepingen naar binnen. | Een concave vorm heeft ten minste één naar binnen wijzend gedeelte, wat de aanwezigheid van een deuk aangeeft. |
| In een convexe veelhoek zijn alle interne hoeken kleiner dan 180°. | In een concave veelhoek bestaat er minstens één binnenhoek groter dan 180°. |
| Elke lijn die twee hoekpunten van een convexe vorm verbindt, ligt volledig binnen de grenzen van de vorm. | De lijn die twee hoekpunten van een concave vorm verbindt, kan al dan niet de binnenkant van de vorm snijden. |
Veelhoeken op basis van grenzen
Veelhoeken kunnen op basis van de aard van hun grenzen worden onderverdeeld in twee primaire typen:
- Eenvoudige veelhoek
- Complexe veelhoek
Eenvoudige veelhoek
Een eenvoudige veelhoek wordt gekenmerkt door een enkelvoudige, niet-kruisende grens. Met andere woorden, het kruist zichzelf niet en bestaat uit één grens.
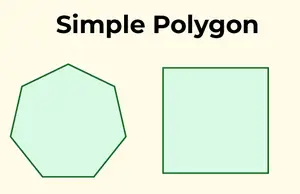
Eenvoudige veelhoeken
Complexe veelhoek
Aan de andere kant wordt een complexe polygoon gedefinieerd door zichzelf te snijden. Het bestaat uit meer dan één grens binnen zijn structuur. Bij complexe polygonen kruisen de grenzen elkaar, waardoor er meerdere afzonderlijke gebieden binnen de polygoon ontstaan.

Complexe veelhoek
Lees meer over Soorten veelhoeken.
Veelhoekformules
Er zijn verschillende formules gerelateerd aan veelhoeken in de geometrie. Enkele van de meest gebruikte zijn:
- Gebiedsformule
- Omtrekformule
- Aantal diagonalen
Alle formules met betrekking tot verschillende polygonen worden hieronder besproken:
js globale variabele
Gebied van veelhoeken
Gebied van een veelhoek vertegenwoordigt de totale ruimte die het inneemt in een tweedimensionaal vlak, wordt bepaald door specifieke formules op basis van het aantal zijden en de classificatie van de veelhoek. De gebiedsformules zijn als volgt:
| Gebied van veelhoek | Formule |
|---|---|
| Gebied van Driehoek | 1/2 × Basis × Hoogte |
| Gebied van het parallellogram | Basis x hoogte |
| Gebied van een rechthoek | Lengte x breedte |
| Gebied van het plein | (Kant)2 |
| 1/2 × diagonaal1× diagonaal2 | |
| Gebied van Trapezium | 1/2 × Hoogte × Som van parallelle zijden |
| (5/2) × lengte zijkant × Apothem | |
| Gebied van zeshoek | {(3√3)/2}zijde2 |
| Gebied van Heptagon | 3.643 × zijkant2 |
Omtrek van veelhoeken
De omtrek van een tweedimensionale vorm vertegenwoordigt de totale lengte van de buitengrens. Voor veelhoeken wordt de omtrek als volgt berekend:
| Omtrek van veelhoek | Formule |
|---|---|
| Omtrek van de driehoek | Som van drie zijden |
| Omtrek van parallellogram | 2(Som van aangrenzende zijden) |
| Omtrek van rechthoek | 2(lengte + breedte) |
| Omtrek van het vierkant | 4 × zijkant |
| Omtrek van Ruit | 4 × zijkant Java-verzamelingsframework |
| Omtrek van trapezium | Som van parallelle zijden + som van niet-parallelle zijden |
| Omtrek van het Pentagon | 5 × zijkant |
| Omtrek van zeshoek | 6 × zijkant |
| Omtrek van zevenhoek | 7 × zijkant |
Diagonaal van veelhoekformule
Een diagonaal van een veelhoek is een lijnsegment dat wordt gevormd door twee hoekpunten die niet aangrenzend zijn, met elkaar te verbinden.
Aantal diagonalen in een veelhoek = n(n−3)/2,
Waar ‘n’ het aantal zijden vertegenwoordigt dat de polygoon bezit.
Lees meer over Diagonaal van veelhoekformule .
Hoeken in veelhoeken
In de meetkunde verwijzen hoeken in veelhoeken naar de hoeken die worden gevormd door de zijkanten van een veelhoek, zowel aan de binnenkant als aan de buitenkant van de veelhoek. Er kunnen dus beide hoeken in een veelhoek zijn, dat wil zeggen:
- Binnenhoeken
- Buitenhoeken
Laten we de formule voor deze hoeken als volgt in detail bespreken:
Formule voor de binnenhoek van veelhoeken
De binnenhoeken van een veelhoek zijn de hoeken die worden gevormd tussen de aangrenzende zijden en zijn gelijk in het geval van een regelmatige veelhoek. Het aantal binnenhoeken komt overeen met het aantal zijden van de veelhoek.
De som van de binnenhoeken ‘S’ in een veelhoek met ‘n’ zijden wordt berekend als
S = (n – 2) × 180°
Waar ‘n’ het aantal zijden vertegenwoordigt.
Buitenhoekformule van veelhoeken
Elke buitenhoek van een regelmatige veelhoek wordt gevormd door het verlengen van een van de zijden (met de klok mee of tegen de klok in) en het meten van de hoek tussen deze verlenging en de aangrenzende zijde. In een regelmatige veelhoek zijn alle buitenhoeken gelijk
De totale som van de buitenhoeken in elke polygoon is vastgesteld op 360°
Daarom,
Elke buitenhoek wordt gegeven door 360°/n
Waarbij ‘n’ het aantal zijden is.
De som van de binnen- en overeenkomstige buitenhoeken op elk hoekpunt in een veelhoek is altijd 180 graden, wat een aanvullende relatie tot uitdrukking brengt:
Binnenhoek + Buitenhoek = 180°
Buitenhoek = 180° – Binnenhoek
Conclusie
- Veelhoek is een gesloten figuur begrensd door drie of meer lijnsegmenten
- Som van binnenhoeken: De som van alle binnenhoeken in een n-zijdige veelhoek wordt gegeven door de formule (n–2)×180°.
- Aantal diagonalen: Voor een veelhoek met n zijden wordt het aantal diagonalen berekend met de formule n(n–3)/2.
- Driehoeken gevormd door diagonalen: Het aantal driehoeken dat wordt gevormd door diagonalen vanuit een enkele hoek van een veelhoek met elkaar te verbinden, is n–2.
- Binnenhoek van regelmatige veelhoek: De maat voor elke binnenhoek in een n-zijdige regelmatige veelhoek is {(n–2)×180°}/n.
- Buitenhoek van regelmatige veelhoek: De maat voor elke buitenhoek in een n-zijdige regelmatige veelhoek is 360°/n.
Lees ook
- Vierkant
- Parallellogram
- Rechthoek
Opgeloste voorbeelden van veelhoeken in wiskunde
Voorbeeld 1: Beschouw een vierhoek met vier zijden. Vind de som van al zijn binnenhoeken van de vierhoek.
Oplossing:
Formule voor de som van binnenhoeken in een n-zijdige regelmatige veelhoek = (n − 2) × 180°
De som van alle binnenhoeken van de vierhoek = (4 – 2) × 180°
De som van alle binnenhoeken van de vierhoek = 2 × 180°
De som van alle binnenhoeken van de vierhoek = 360°
Daarom is de som van alle binnenhoeken van de vierhoek 360°.
Voorbeeld 2: Beschouw een regelmatige veelhoek met een gegeven buiten- en binnenhoekverhouding van 7:3. Bepaal het type polygoon.
Oplossing:
De verhouding tussen de buiten- en binnenhoek is 7:3.
Neem aan dat de buiten- en binnenhoek van een veelhoek 7x en 3x zijn.
De som van de buiten- en binnenhoeken van elke polygoon is 180°.
7x + 3x = 180°
10x = 180°
x = 18°
Buitenhoek = 18°
Aantal zijden = 360°/buitenhoek
= 360°/18°
= 20
Daarom is de gegeven polygoon een icosagon, aangezien deze 20 zijden heeft.
Voorbeeld 3: Elke buitenhoek van een polygoon meet 90 graden. Bepaal het type polygoon?
Oplossing:
Volgens de formule is elke buitenhoek = 360°/n
Hier n=aantal zijden.
90°= 360°/n
n = 360°/90°= 4
De polygoon in kwestie is dus een vierhoek, omdat deze vier zijden heeft.
Voorbeeld 4: De zijkanten zijn 10m, 10m, 8m, 8m, 5m, 5m, 9m, 9m. Hoeveel meter touw is er nodig voor de perimeter?
Oplossing:
Om de lengte van het touw te vinden die nodig is voor de omtrek, moeten we de lengtes van alle zijden bij elkaar optellen:
Omtrek = 10 m + 10 m + 8 m + 8 m + 5 m + 5 m + 9 m + 9 m
Omtrek = 64 m.
shellscript uitvoerbaar makenEr zal dus in totaal 64 meter touw nodig zijn voor de Perimeter.
Oefenvragen over veelhoeken in de meetkunde
Hieronder volgen enkele oefenvragen gebaseerd op de formule van polygonen:
Q1. Gegeven dat één hoek van een vijfhoek 140° is, bepaal dan de grootte van de grootste hoek als de overige hoeken een verhouding hebben van 1:2:3:4.
Vraag 2. Als de som van de binnenhoeken van een veelhoek 160° is, bereken dan het aantal zijden van de veelhoek.
Q3. Het aantal zijden van twee regelmatige veelhoeken heeft een verhouding van 2:3, en de verhouding van hun binnenhoeken is 4:5. Zoek het respectievelijke aantal zijden van deze veelhoeken.
Q4. Bepaal de totale som van de hoeken in een zevenhoek.
Vraag 5. Bereken de som van de buitenhoeken in een vijfhoek.
Vraag 6. Hoeveel zijden heeft een zeshoek?
- 4
- 6
- 8
- 10
Vraag 7. Welke van de volgende is geen regelmatige veelhoek?
- Driehoek
- Vierkant
- Pentagon
- Parallellogram
Veelgestelde vragen over polygonen in wiskunde
Wat is een veelhoek in wiskunde?
In de wiskunde verwijst een veelhoek naar een gesloten tweedimensionale figuur gevormd door de verbinding van drie of meer rechte lijnen. De term polygoon is afgeleid van de Griekse taal, waarbij poly-veel betekent en gon hoek.
Wat is de kleinste veelhoek?
De kleinste gevormde veelhoek is een driehoek met drie zijden.
Wat is 20-gon?
Een 20-hoek is een twintigzijdige veelhoek in de geometrie.
Wat is de totale som van de externe hoeken van de veelhoek?
De som van de buitenhoeken van een veelhoek is 360°.
Kan een cirkel worden geclassificeerd als een veelhoek?
Veelhoek is een gesloten vorm die bestaat uit rechte lijnsegmenten. De cirkel is een gesloten figuur, maar bestaat uit een curve. Een cirkel is dus geen veelhoek.
Wat is de som van de binnenhoek van een veelhoek?
De som van de binnenhoek van een veelhoek wordt gegeven door (n–2)×180°, waarbij n het aantal zijden in de veelhoek is.
