In de informatica bestaan er enkele problemen waarvan de oplossing nog niet is gevonden; de problemen zijn onderverdeeld in klassen die bekend staan als Complexiteitsklassen . In de complexiteitstheorie is een complexiteitsklasse een reeks problemen met gerelateerde complexiteit. Deze lessen helpen wetenschappers problemen te groeperen op basis van de hoeveelheid tijd en ruimte die ze nodig hebben om problemen op te lossen en de oplossingen te verifiëren. Het is de tak van de rekentheorie die zich bezighoudt met de middelen die nodig zijn om een probleem op te lossen.
afbeelding uitlijnen met css
De gemeenschappelijke bronnen zijn tijd en ruimte, dat wil zeggen hoeveel tijd het algoritme nodig heeft om een probleem op te lossen en het bijbehorende geheugengebruik.
- De tijdscomplexiteit van een algoritme wordt gebruikt om het aantal stappen te beschrijven dat nodig is om een probleem op te lossen, maar kan ook worden gebruikt om te beschrijven hoe lang het duurt om het antwoord te verifiëren.
- De ruimtecomplexiteit van een algoritme beschrijft hoeveel geheugen nodig is om het algoritme te laten werken.
Complexiteitsklassen zijn nuttig bij het organiseren van vergelijkbare soorten problemen.
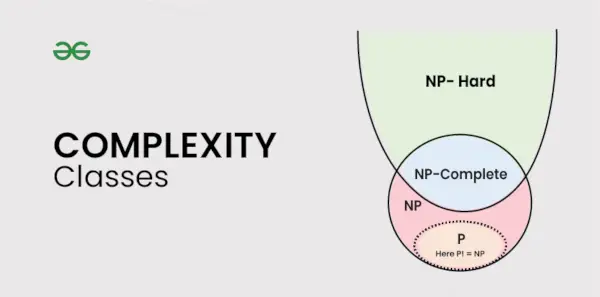
Soorten complexiteitsklassen
In dit artikel worden de volgende complexiteitsklassen besproken:
- P-Klasse
- NP-klasse
- CoNP-klasse
- NP-hard
- NP-compleet
P-Klasse
De P in de P-klasse staat voor Polynomische tijd. Het is de verzameling beslissingsproblemen (problemen met een ja of nee antwoord) die door een deterministische machine in polynomiale tijd kunnen worden opgelost.
Functies:
- De oplossing voor P-probleem s is gemakkelijk te vinden.
- P is vaak een klasse van computerproblemen die oplosbaar en handelbaar zijn. Handelbaar betekent dat de problemen zowel in theorie als in de praktijk oplosbaar zijn. Maar de problemen die in theorie wel, maar in de praktijk niet kunnen worden opgelost, staan bekend als hardnekkig.
Deze klasse bevat veel problemen:
- Berekening van de grootste gemene deler.
- Het vinden van een maximale matching.
- Sortering samenvoegen
NP-klasse
De NP in NP-klasse staat voor Niet-deterministische polynomiale tijd . Het is de verzameling beslissingsproblemen die in polynomiale tijd door een niet-deterministische machine kunnen worden opgelost.
Functies:
- De oplossingen van de NP-klasse zijn moeilijk te vinden omdat ze worden opgelost door een niet-deterministische machine, maar de oplossingen zijn eenvoudig te verifiëren.
- Problemen van NP kunnen in polynomiale tijd worden geverifieerd door een Turing-machine.
Voorbeeld:
Laten we een voorbeeld bekijken om het beter te begrijpen NP-klasse . Stel dat er een bedrijf is met een totaal van 1000 werknemers met een unieke werknemer ID's . Neem aan dat die er zijn 200 kamers voor hen beschikbaar. Een selectie van 200 werknemers moeten aan elkaar worden gekoppeld, maar de CEO van het bedrijf beschikt over de gegevens van enkele werknemers die om persoonlijke redenen niet in dezelfde ruimte kunnen werken.
Dit is een voorbeeld van een BIJV probleem. Omdat het gemakkelijk is om te controleren of de gegeven keuze is 200 werknemers voorgesteld door een collega zijn bevredigend of niet, d.w.z. geen enkel paar uit de collega-lijst verschijnt op de lijst die door de CEO wordt verstrekt. Maar het genereren van een dergelijke lijst vanuit het niets lijkt zo moeilijk dat het volkomen onpraktisch is.
Het geeft aan dat als iemand ons de oplossing voor het probleem kan bieden, we het juiste en onjuiste paar in polynomiale tijd kunnen vinden. Dus voor de BIJV klassenprobleem is het antwoord mogelijk, dat in polynomiale tijd kan worden berekend.
Java-arrays
Deze les bevat veel problemen die je graag effectief zou willen oplossen:
- Booleaans tevredenheidsprobleem (SAT).
- Hamiltoniaans padprobleem.
- Grafiek kleuren.
Co-NP-klasse
Co-NP staat voor het complement van NP Class. Het betekent dat als het antwoord op een probleem in Co-NP Nee is, er bewijs is dat in polynomiale tijd kan worden gecontroleerd.
Functies:
- Als een probleem X zich in NP bevindt, dan bevindt zijn complement X’ zich ook in CoNP.
- Voor een NP- en CoNP-probleem is het niet nodig om alle antwoorden tegelijk in polynomiale tijd te verifiëren; er hoeft slechts één bepaald antwoord ja of nee in polynomiale tijd te worden geverifieerd voordat een probleem in NP of CoNP kan voorkomen.
Enkele voorbeeldproblemen voor CoNP zijn:
- Om het priemgetal te controleren.
- Factorisatie van gehele getallen.
NP-harde klasse
Een NP-moeilijk probleem is minstens zo moeilijk als het moeilijkste probleem in NP en het is een klasse van problemen waarbij elk probleem in NP wordt gereduceerd tot NP-moeilijk.
Functies:
Java-methode
- Alle NP-harde problemen bevinden zich niet in NP.
- Het duurt lang om ze te controleren. Dit betekent dat als er een oplossing voor een NP-moeilijk probleem wordt gegeven, het lang duurt om te controleren of deze klopt of niet.
- Een probleem A is in NP-moeilijk als er voor elk probleem L in NP een polynomiale tijdsreductie bestaat van L naar A.
Enkele voorbeelden van problemen in Np-hard zijn:
- Probleem met stoppen.
- Gekwalificeerde Booleaanse formules.
- Geen Hamiltoniaanse cyclus.
NP-complete klasse
Een probleem is NP-compleet als het zowel NP als NP-moeilijk is. NP-volledige problemen zijn de harde problemen in NP.
Functies:
- NP-complete problemen zijn speciaal omdat elk probleem in de NP-klasse in polynomiale tijd kan worden getransformeerd of gereduceerd tot NP-complete problemen.
- Als je een NP-compleet probleem in polynomiale tijd zou kunnen oplossen, dan zou je ook elk NP-probleem in polynomiale tijd kunnen oplossen.
Enkele voorbeeldproblemen zijn:
- Hamiltoniaanse cyclus.
- Bevredigbaarheid.
- Hoekpunt dekking .
| Complexiteitsklasse | Karakteristieke eigenschap |
| P | Gemakkelijk oplosbaar in polynomiale tijd. |
| BIJV | Ja, antwoorden kunnen in polynomiale tijd worden gecontroleerd. |
| Co-NP | Nee, antwoorden kunnen in polynomiale tijd worden gecontroleerd. |
| NP-hard | Alle NP-harde problemen staan niet in NP en het duurt lang om ze te controleren. |
| NP-compleet | Een probleem dat NP en NP-moeilijk is, is NP-compleet. |
