Wat is Hamiltoniaanse cyclus?
Hamiltoniaanse cyclus of circuit in een grafiek G is een cyclus die elk hoekpunt van bezoekt G precies één keer en keert terug naar het startpunt.
- Als de grafiek een Hamiltoniaanse cyclus bevat, wordt deze genoemd Hamiltoniaanse grafiek anders is het zo niet-Hamiltoniaans .
- Het vinden van een Hamiltoniaanse cyclus in een grafiek is een bekend gegeven NP-volledig probleem , wat betekent dat er geen efficiënt algoritme bekend is om het voor alle soorten grafieken op te lossen. Het kan echter worden opgelost voor kleine of specifieke soorten grafieken.
Het Hamiltoniaanse cyclusprobleem heeft praktische toepassingen op verschillende gebieden, zoals logistiek, netwerkontwerp en informatica .
Wat is Hamiltoniaans pad?
Hamiltoniaans pad in een grafiek G is een pad dat elk hoekpunt van G precies één keer en bezoekt Hamiltoniaans pad hoeft niet terug te keren naar het startpunt. Het is een open pad.
- Vergelijkbaar met de Hamiltoniaanse cyclus probleem, het vinden van een Hamiltoniaans pad in een algemene grafiek is dat ook het geval NP-compleet en kan een uitdaging zijn. Het is echter vaak een eenvoudiger probleem dan het vinden van een Hamiltoniaanse cyclus.
- Hamiltoniaanse paden hebben toepassingen op verschillende gebieden, zoals het vinden van optimale routes in transportnetwerken, circuitontwerp en onderzoek naar grafentheorie .
Problemen Verklaring: Gegeven een ongerichte grafiek, is het de taak om te bepalen of de grafiek een Hamiltoniaanse cyclus bevat of niet. Als dit het pad bevat, wordt het pad afgedrukt.
Voorbeeld:
Aanbevolen: los het op OEFENING eerst, voordat u verder gaat met de oplossing.Invoer: grafiek[][] = {{0, 1, 0, 1, 0},{1, 0, 1, 1, 1},{0, 1, 0, 0, 1},{1, 1, 0, 0, 1},{0, 1, 1, 1, 0}}
Invoergrafiek[][]
tekstomslag cssUitgang: {0, 1, 2, 4, 3, 0}.
Invoer: grafiek[][] = {{0, 1, 0, 1, 0},{1, 0, 1, 1, 1},{0, 1, 0, 0, 1},{1, 1, 0, 0, 0},{0, 1, 1, 0, 0}}
Invoergrafiek[][]
Uitgang: Oplossing bestaat niet
Naïef algoritme : Dit probleem kan worden opgelost met behulp van het onderstaande idee:
Genereer alle mogelijke configuraties van hoekpunten en druk een configuratie af die aan de gegeven beperkingen voldoet. Er zal n zijn! (n faculteit) configuraties. Dus de algehele tijdscomplexiteit van deze aanpak zal dat zijn OP!).
Hamiltoniaanse cyclus gebruikt Backtracking-algoritme :
Maak een lege padarray en voeg hoekpunt toe 0 ernaar. Voeg andere hoekpunten toe, beginnend bij het hoekpunt 1 . Voordat u een hoekpunt toevoegt, controleert u of dit grenst aan het eerder toegevoegde hoekpunt en niet al is toegevoegd. Als we zo'n hoekpunt vinden, voegen we het hoekpunt toe als onderdeel van de oplossing. Als we geen hoekpunt vinden, keren we terug vals .
Illustraties:
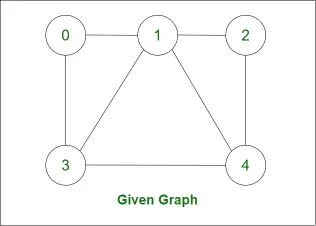
Laten we de Hamiltoniaanse cyclus voor de volgende grafiek bekijken:
- Begin met het knooppunt 0 .
- Pas DFS toe om het Hamiltoniaanse pad te vinden.
- Wanneer het basisscenario wordt bereikt (d.w.z. totaal aantal doorlopen knooppunten == V (totaal hoekpunt) ):
- Controleer of het huidige knooppunt een buur is van het startknooppunt.
- Als knooppunt 2 en knooppunt 0 zijn geen buren van elkaar, dus keer ervan terug.
Vanaf startknooppunt 0 wordt DFS aangeroepen
- Omdat cyclus niet wordt gevonden in pad {0, 3, 1, 4, 2}. Dus keer terug van knooppunt 2, knooppunt 4.
- Onderzoek nu een andere optie voor knooppunt 1 (dat wil zeggen knooppunt 2)
- Wanneer de basisconditie opnieuw wordt bereikt, controleer dan de Hamiltoniaanse cyclus
- Omdat knooppunt 4 niet de buurman is van knooppunt 0, wordt de cyclus opnieuw niet gevonden en keert u terug.
- Terugkeer van knooppunt 4, knooppunt 2, knooppunt 1.
- Ontdek nu andere opties voor knooppunt 3.
Hamiltoniaanse cyclus
- Op het Hamiltoniaanse pad {0,3,4,2,1,0} we krijgen een cyclus omdat knooppunt 1 de buurman is van knooppunt 0.
- Print dus dit fietspad.
- Dit is onze Hamiltoniaanse cyclus.
Hieronder vindt u de Backtracking-implementatie voor het vinden van de Hamiltoniaanse cyclus:
C++ /* C++ program for solution of Hamiltonian Cycle problem using backtracking */ #include using namespace std; // Number of vertices in the graph #define V 5 void printSolution(int path[]); /* A utility function to check if the vertex v can be added at index 'pos' in the Hamiltonian Cycle constructed so far (stored in 'path[]') */ bool isSafe(int v, bool graph[V][V], int path[], int pos) { /* Check if this vertex is an adjacent vertex of the previously added vertex. */ if (graph [path[pos - 1]][ v ] == 0) return false; /* Check if the vertex has already been included. This step can be optimized by creating an array of size V */ for (int i = 0; i < pos; i++) if (path[i] == v) return false; return true; } /* A recursive utility function to solve hamiltonian cycle problem */ bool hamCycleUtil(bool graph[V][V], int path[], int pos) { /* base case: If all vertices are included in Hamiltonian Cycle */ if (pos == V) { // And if there is an edge from the // last included vertex to the first vertex if (graph[path[pos - 1]][path[0]] == 1) return true; else return false; } // Try different vertices as a next candidate // in Hamiltonian Cycle. We don't try for 0 as // we included 0 as starting point in hamCycle() for (int v = 1; v < V; v++) { /* Check if this vertex can be added // to Hamiltonian Cycle */ if (isSafe(v, graph, path, pos)) { path[pos] = v; /* recur to construct rest of the path */ if (hamCycleUtil (graph, path, pos + 1) == true) return true; /* If adding vertex v doesn't lead to a solution, then remove it */ path[pos] = -1; } } /* If no vertex can be added to Hamiltonian Cycle constructed so far, then return false */ return false; } /* This function solves the Hamiltonian Cycle problem using Backtracking. It mainly uses hamCycleUtil() to solve the problem. It returns false if there is no Hamiltonian Cycle possible, otherwise return true and prints the path. Please note that there may be more than one solutions, this function prints one of the feasible solutions. */ bool hamCycle(bool graph[V][V]) { int *path = new int[V]; for (int i = 0; i < V; i++) path[i] = -1; /* Let us put vertex 0 as the first vertex in the path. If there is a Hamiltonian Cycle, then the path can be started from any point of the cycle as the graph is undirected */ path[0] = 0; if (hamCycleUtil(graph, path, 1) == false ) { cout << '
Solution does not exist'; return false; } printSolution(path); return true; } /* A utility function to print solution */ void printSolution(int path[]) { cout << 'Solution Exists:' ' Following is one Hamiltonian Cycle
'; for (int i = 0; i < V; i++) cout << path[i] << ' '; // Let us print the first vertex again // to show the complete cycle cout << path[0] << ' '; cout << endl; } // Driver Code int main() { /* Let us create the following graph (0)--(1)--(2) | / | | / | | / | (3)-------(4) */ bool graph1[V][V] = {{0, 1, 0, 1, 0}, {1, 0, 1, 1, 1}, {0, 1, 0, 0, 1}, {1, 1, 0, 0, 1}, {0, 1, 1, 1, 0}}; // Print the solution hamCycle(graph1); /* Let us create the following graph (0)--(1)--(2) | / | | / | | / | (3) (4) */ bool graph2[V][V] = {{0, 1, 0, 1, 0}, {1, 0, 1, 1, 1}, {0, 1, 0, 0, 1}, {1, 1, 0, 0, 0}, {0, 1, 1, 0, 0}}; // Print the solution hamCycle(graph2); return 0; } // This is code is contributed by rathbhupendra> C++ #include using namespace std; int main() { cout << 'GFG!'; return 0; }> C /* C program for solution of Hamiltonian Cycle problem using backtracking */ #include // Number of vertices in the graph #define V 5 void printSolution(int path[]); /* A utility function to check if the vertex v can be added at index 'pos' in the Hamiltonian Cycle constructed so far (stored in 'path[]') */ int isSafe(int v, int graph[V][V], int path[], int pos) { /* Check if this vertex is an adjacent vertex of the previously added vertex. */ if (graph [ path[pos-1] ][ v ] == 0) return 0; /* Check if the vertex has already been included. This step can be optimized by creating an array of size V */ for (int i = 0; i < pos; i++) if (path[i] == v) return 0; return 1; } /* A recursive utility function to solve hamiltonian cycle problem */ int hamCycleUtil(int graph[V][V], int path[], int pos) { /* base case: If all vertices are included in Hamiltonian Cycle */ if (pos == V) { // And if there is an edge from the last included vertex to the // first vertex if ( graph[ path[pos-1] ][ path[0] ] == 1 ) return 1; else return 0; } // Try different vertices as a next candidate in Hamiltonian Cycle. // We don't try for 0 as we included 0 as starting point in hamCycle() for (int v = 1; v < V; v++) { /* Check if this vertex can be added to Hamiltonian Cycle */ if (isSafe(v, graph, path, pos)) { path[pos] = v; /* recur to construct rest of the path */ if (hamCycleUtil (graph, path, pos+1) == 1) return 1; /* If adding vertex v doesn't lead to a solution, then remove it */ path[pos] = -1; } } /* If no vertex can be added to Hamiltonian Cycle constructed so far, then return false */ return 0; } /* This function solves the Hamiltonian Cycle problem using Backtracking. It mainly uses hamCycleUtil() to solve the problem. It returns false if there is no Hamiltonian Cycle possible, otherwise return true and prints the path. Please note that there may be more than one solutions, this function prints one of the feasible solutions. */ int hamCycle(int graph[V][V]) { int path[V]; for (int i = 0; i < V; i++) path[i] = -1; /* Let us put vertex 0 as the first vertex in the path. If there is a Hamiltonian Cycle, then the path can be started from any point of the cycle as the graph is undirected */ path[0] = 0; if ( hamCycleUtil(graph, path, 1) == 0 ) { printf('
Solution does not exist'); return 0; } printSolution(path); return 1; } /* A utility function to print solution */ void printSolution(int path[]) { printf ('Solution Exists:' ' Following is one Hamiltonian Cycle
'); for (int i = 0; i < V; i++) printf(' %d ', path[i]); // Let us print the first vertex again to show the complete cycle printf(' %d ', path[0]); printf('
'); } // driver program to test above function int main() { /* Let us create the following graph (0)--(1)--(2) | / | | / | | / | (3)-------(4) */ int graph1[V][V] = {{0, 1, 0, 1, 0}, {1, 0, 1, 1, 1}, {0, 1, 0, 0, 1}, {1, 1, 0, 0, 1}, {0, 1, 1, 1, 0}, }; // Print the solution hamCycle(graph1); /* Let us create the following graph (0)--(1)--(2) | / | | / | | / | (3) (4) */ int graph2[V][V] = {{0, 1, 0, 1, 0}, {1, 0, 1, 1, 1}, {0, 1, 0, 0, 1}, {1, 1, 0, 0, 0}, {0, 1, 1, 0, 0}, }; // Print the solution hamCycle(graph2); return 0; }> Java /* Java program for solution of Hamiltonian Cycle problem using backtracking */ class HamiltonianCycle { final int V = 5; int path[]; /* A utility function to check if the vertex v can be added at index 'pos'in the Hamiltonian Cycle constructed so far (stored in 'path[]') */ boolean isSafe(int v, int graph[][], int path[], int pos) { /* Check if this vertex is an adjacent vertex of the previously added vertex. */ if (graph[path[pos - 1]][v] == 0) return false; /* Check if the vertex has already been included. This step can be optimized by creating an array of size V */ for (int i = 0; i < pos; i++) if (path[i] == v) return false; return true; } /* A recursive utility function to solve hamiltonian cycle problem */ boolean hamCycleUtil(int graph[][], int path[], int pos) { /* base case: If all vertices are included in Hamiltonian Cycle */ if (pos == V) { // And if there is an edge from the last included // vertex to the first vertex if (graph[path[pos - 1]][path[0]] == 1) return true; else return false; } // Try different vertices as a next candidate in // Hamiltonian Cycle. We don't try for 0 as we // included 0 as starting point in hamCycle() for (int v = 1; v < V; v++) { /* Check if this vertex can be added to Hamiltonian Cycle */ if (isSafe(v, graph, path, pos)) { path[pos] = v; /* recur to construct rest of the path */ if (hamCycleUtil(graph, path, pos + 1) == true) return true; /* If adding vertex v doesn't lead to a solution, then remove it */ path[pos] = -1; } } /* If no vertex can be added to Hamiltonian Cycle constructed so far, then return false */ return false; } /* This function solves the Hamiltonian Cycle problem using Backtracking. It mainly uses hamCycleUtil() to solve the problem. It returns false if there is no Hamiltonian Cycle possible, otherwise return true and prints the path. Please note that there may be more than one solutions, this function prints one of the feasible solutions. */ int hamCycle(int graph[][]) { path = new int[V]; for (int i = 0; i < V; i++) path[i] = -1; /* Let us put vertex 0 as the first vertex in the path. If there is a Hamiltonian Cycle, then the path can be started from any point of the cycle as the graph is undirected */ path[0] = 0; if (hamCycleUtil(graph, path, 1) == false) { System.out.println('
Solution does not exist'); return 0; } printSolution(path); return 1; } /* A utility function to print solution */ void printSolution(int path[]) { System.out.println('Solution Exists: Following' + ' is one Hamiltonian Cycle'); for (int i = 0; i < V; i++) System.out.print(' ' + path[i] + ' '); // Let us print the first vertex again to show the // complete cycle System.out.println(' ' + path[0] + ' '); } // driver program to test above function public static void main(String args[]) { HamiltonianCycle hamiltonian = new HamiltonianCycle(); /* Let us create the following graph (0)--(1)--(2) | / | | / | | / | (3)-------(4) */ int graph1[][] = {{0, 1, 0, 1, 0}, {1, 0, 1, 1, 1}, {0, 1, 0, 0, 1}, {1, 1, 0, 0, 1}, {0, 1, 1, 1, 0}, }; // Print the solution hamiltonian.hamCycle(graph1); /* Let us create the following graph (0)--(1)--(2) | / | | / | | / | (3) (4) */ int graph2[][] = {{0, 1, 0, 1, 0}, {1, 0, 1, 1, 1}, {0, 1, 0, 0, 1}, {1, 1, 0, 0, 0}, {0, 1, 1, 0, 0}, }; // Print the solution hamiltonian.hamCycle(graph2); } } // This code is contributed by Abhishek Shankhadhar> Python # Python program for solution of # hamiltonian cycle problem class Graph(): def __init__(self, vertices): self.graph = [[0 for column in range(vertices)] for row in range(vertices)] self.V = vertices ''' Check if this vertex is an adjacent vertex of the previously added vertex and is not included in the path earlier ''' def isSafe(self, v, pos, path): # Check if current vertex and last vertex # in path are adjacent if self.graph[ path[pos-1] ][v] == 0: return False # Check if current vertex not already in path for vertex in path: if vertex == v: return False return True # A recursive utility function to solve # hamiltonian cycle problem def hamCycleUtil(self, path, pos): # base case: if all vertices are # included in the path if pos == self.V: # Last vertex must be adjacent to the # first vertex in path to make a cycle if self.graph[ path[pos-1] ][ path[0] ] == 1: return True else: return False # Try different vertices as a next candidate # in Hamiltonian Cycle. We don't try for 0 as # we included 0 as starting point in hamCycle() for v in range(1,self.V): if self.isSafe(v, pos, path) == True: path[pos] = v if self.hamCycleUtil(path, pos+1) == True: return True # Remove current vertex if it doesn't # lead to a solution path[pos] = -1 return False def hamCycle(self): path = [-1] * self.V ''' Let us put vertex 0 as the first vertex in the path. If there is a Hamiltonian Cycle, then the path can be started from any point of the cycle as the graph is undirected ''' path[0] = 0 if self.hamCycleUtil(path,1) == False: print ('Solution does not exist
') return False self.printSolution(path) return True def printSolution(self, path): print ('Solution Exists: Following', 'is one Hamiltonian Cycle') for vertex in path: print (vertex ) # Driver Code ''' Let us create the following graph (0)--(1)--(2) | / | | / | | / | (3)-------(4) ''' g1 = Graph(5) g1.graph = [ [0, 1, 0, 1, 0], [1, 0, 1, 1, 1], [0, 1, 0, 0, 1,],[1, 1, 0, 0, 1], [0, 1, 1, 1, 0], ] # Print the solution g1.hamCycle(); ''' Let us create the following graph (0)--(1)--(2) | / | | / | | / | (3) (4) ''' g2 = Graph(5) g2.graph = [ [0, 1, 0, 1, 0], [1, 0, 1, 1, 1], [0, 1, 0, 0, 1,], [1, 1, 0, 0, 0], [0, 1, 1, 0, 0], ] # Print the solution g2.hamCycle(); # This code is contributed by Divyanshu Mehta> C# // C# program for solution of Hamiltonian // Cycle problem using backtracking using System; public class HamiltonianCycle { readonly int V = 5; int []path; /* A utility function to check if the vertex v can be added at index 'pos'in the Hamiltonian Cycle constructed so far (stored in 'path[]') */ bool isSafe(int v, int [,]graph, int []path, int pos) { /* Check if this vertex is an adjacent vertex of the previously added vertex. */ if (graph[path[pos - 1], v] == 0) return false; /* Check if the vertex has already been included. This step can be optimized by creating an array of size V */ for (int i = 0; i < pos; i++) if (path[i] == v) return false; return true; } /* A recursive utility function to solve hamiltonian cycle problem */ bool hamCycleUtil(int [,]graph, int []path, int pos) { /* base case: If all vertices are included in Hamiltonian Cycle */ if (pos == V) { // And if there is an edge from the last included // vertex to the first vertex if (graph[path[pos - 1],path[0]] == 1) return true; else return false; } // Try different vertices as a next candidate in // Hamiltonian Cycle. We don't try for 0 as we // included 0 as starting point in hamCycle() for (int v = 1; v < V; v++) { /* Check if this vertex can be added to Hamiltonian Cycle */ if (isSafe(v, graph, path, pos)) { path[pos] = v; /* recur to construct rest of the path */ if (hamCycleUtil(graph, path, pos + 1) == true) return true; /* If adding vertex v doesn't lead to a solution, then remove it */ path[pos] = -1; } } /* If no vertex can be added to Hamiltonian Cycle constructed so far, then return false */ return false; } /* This function solves the Hamiltonian Cycle problem using Backtracking. It mainly uses hamCycleUtil() to solve the problem. It returns false if there is no Hamiltonian Cycle possible, otherwise return true and prints the path. Please note that there may be more than one solutions, this function prints one of the feasible solutions. */ int hamCycle(int [,]graph) { path = new int[V]; for (int i = 0; i < V; i++) path[i] = -1; /* Let us put vertex 0 as the first vertex in the path. If there is a Hamiltonian Cycle, then the path can be started from any point of the cycle as the graph is undirected */ path[0] = 0; if (hamCycleUtil(graph, path, 1) == false) { Console.WriteLine('
Solution does not exist'); return 0; } printSolution(path); return 1; } /* A utility function to print solution */ void printSolution(int []path) { Console.WriteLine('Solution Exists: Following' + ' is one Hamiltonian Cycle'); for (int i = 0; i < V; i++) Console.Write(' ' + path[i] + ' '); // Let us print the first vertex again // to show the complete cycle Console.WriteLine(' ' + path[0] + ' '); } // Driver code public static void Main(String []args) { HamiltonianCycle hamiltonian = new HamiltonianCycle(); /* Let us create the following graph (0)--(1)--(2) | / | | / | | / | (3)-------(4) */ int [,]graph1= {{0, 1, 0, 1, 0}, {1, 0, 1, 1, 1}, {0, 1, 0, 0, 1}, {1, 1, 0, 0, 1}, {0, 1, 1, 1, 0}, }; // Print the solution hamiltonian.hamCycle(graph1); /* Let us create the following graph (0)--(1)--(2) | / | | / | | / | (3) (4) */ int [,]graph2 = {{0, 1, 0, 1, 0}, {1, 0, 1, 1, 1}, {0, 1, 0, 0, 1}, {1, 1, 0, 0, 0}, {0, 1, 1, 0, 0}, }; // Print the solution hamiltonian.hamCycle(graph2); } } // This code contributed by Rajput-Ji> Javascript >
PHP // PHP program for solution of // Hamiltonian Cycle problem // using backtracking $V = 5; /* A utility function to check if the vertex v can be added at index 'pos' in the Hamiltonian Cycle constructed so far (stored in 'path[]') */ function isSafe($v, $graph, &$path, $pos) { /* Check if this vertex is an adjacent vertex of the previously added vertex. */ if ($graph[$path[$pos - 1]][$v] == 0) return false; /* Check if the vertex has already been included. This step can be optimized by creating an array of size V */ for ($i = 0; $i < $pos; $i++) if ($path[$i] == $v) return false; return true; } /* A recursive utility function to solve hamiltonian cycle problem */ function hamCycleUtil($graph, &$path, $pos) { global $V; /* base case: If all vertices are included in Hamiltonian Cycle */ if ($pos == $V) { // And if there is an edge from the // last included vertex to the first vertex if ($graph[$path[$pos - 1]][$path[0]] == 1) return true; else return false; } // Try different vertices as a next candidate in // Hamiltonian Cycle. We don't try for 0 as we // included 0 as starting point hamCycle() for ($v = 1; $v < $V; $v++) { /* Check if this vertex can be added to Hamiltonian Cycle */ if (isSafe($v, $graph, $path, $pos)) { $path[$pos] = $v; /* recur to construct rest of the path */ if (hamCycleUtil($graph, $path, $pos + 1) == true) return true; /* If adding vertex v doesn't lead to a solution, then remove it */ $path[$pos] = -1; } } /* If no vertex can be added to Hamiltonian Cycle constructed so far, then return false */ return false; } /* This function solves the Hamiltonian Cycle problem using Backtracking. It mainly uses hamCycleUtil() to solve the problem. It returns false if there is no Hamiltonian Cycle possible, otherwise return true and prints the path. Please note that there may be more than one solutions, this function prints one of the feasible solutions. */ function hamCycle($graph) { global $V; $path = array_fill(0, $V, 0); for ($i = 0; $i < $V; $i++) $path[$i] = -1; /* Let us put vertex 0 as the first vertex in the path. If there is a Hamiltonian Cycle, then the path can be started from any point of the cycle as the graph is undirected */ $path[0] = 0; if (hamCycleUtil($graph, $path, 1) == false) { echo('
Solution does not exist'); return 0; } printSolution($path); return 1; } /* A utility function to print solution */ function printSolution($path) { global $V; echo('Solution Exists: Following is '. 'one Hamiltonian Cycle
'); for ($i = 0; $i < $V; $i++) echo(' '.$path[$i].' '); // Let us print the first vertex again to show the // complete cycle echo(' '.$path[0].'
'); } // Driver Code /* Let us create the following graph (0)--(1)--(2) | / | | / | | / | (3)-------(4) */ $graph1 = array(array(0, 1, 0, 1, 0), array(1, 0, 1, 1, 1), array(0, 1, 0, 0, 1), array(1, 1, 0, 0, 1), array(0, 1, 1, 1, 0), ); // Print the solution hamCycle($graph1); /* Let us create the following graph (0)--(1)--(2) | / | | / | | / | (3) (4) */ $graph2 = array(array(0, 1, 0, 1, 0), array(1, 0, 1, 1, 1), array(0, 1, 0, 0, 1), array(1, 1, 0, 0, 0), array(0, 1, 1, 0, 0)); // Print the solution hamCycle($graph2); // This code is contributed by mits ?>> Uitvoer
Solution Exists: Following is one Hamiltonian Cycle 0 1 2 4 3 0 Solution does not exist>
Tijdcomplexiteit: O(N!), waarbij N het aantal hoekpunten is.
Hulpruimte: O(1), omdat er geen extra ruimte wordt gebruikt.
Opmerking: De bovenstaande code drukt altijd een cyclus af vanaf 0 . Het startpunt zou er niet toe moeten doen, omdat de cyclus vanaf elk punt kan worden gestart. Als u het startpunt wilt wijzigen, moet u twee wijzigingen aanbrengen in de bovenstaande code.
Pad wijzigen[0] = 0; naar pad[0] = s ; waar S is jouw nieuwe startpunt . Verander ook de lus voor (int v = 1; v