Horizontale lijnen worden gedefinieerd als lijnen die evenwijdig lopen aan de horizon of de grond, vandaar de naam horizontale lijn . De horizontale lijn heeft een helling van nul, dat wil zeggen dat de hellingshoek van deze lijnen nul graden is. Als de horizontale lijnen op de Cartesiaanse vlakken worden getekend, snijden ze alleen langs de y-as, omdat ze altijd evenwijdig aan de x-as lopen en deze nooit doorsnijden.
In dit artikel zullen we in detail leren over de horizontale lijn, de eigenschappen ervan, de helling van de horizontale lijn, de vergelijking van de horizontale lijn, voorbeelden en veelgestelde vragen met betrekking tot de horizontale lijnen.
Inhoudsopgave
- Horizontale lijndefinitie
- Helling van horizontale lijn
- Een horizontale lijn tekenen
- Horizontale lijnvergelijking
- Horizontale lijntest
- Horizontale en verticale lijnen
- Verschillen tussen verticale lijnen en horizontale lijnen
- Korte opmerking over horizontale lijn
- Voorbeelden van horizontale lijnen
Horizontale lijndefinitie
We weten dat een lijn een recht pad is dat twee of meer twee punten met elkaar verbindt en tot in het oneindige loopt. We definiëren horizontale lijnen dus als lijnen die parallel lopen aan de grond of de horizon en zich op een constante hoogte vanaf de grond bevinden.
Als we deze lijnen in het Cartesiaanse systeem uitzetten, zijn dit de lijnen die geen snijpunt op de x-as hebben, maar wel een snijpunt op de y-as. Horizontale lijnen hebben een helling van nul, dat wil zeggen dat ze geen hoek hebben met de x-as of de grond.
Horizontale lijnen vormen de basis van de verschillende objecten, vormen en figuren die we in de meetkunde bestuderen. Stel dat we een rechthoek, vierkant, driehoek, trapezium , enz., dan bestaat de basis van deze figuren meestal uit horizontale lijnen. We observeren ook horizontale leugens in het echte leven, aangezien de lijnen op de vloer en het dak van de kamers, de onderkant van de trap, enz. ook door de horizontale lijnen worden gemaakt.
Deze lijnen worden ook wel slaaplijnen genoemd, omdat ze geen verticale beweging hebben en altijd op een constante hoogte ten opzichte van de grond blijven. De onderstaande afbeelding toont de horizontale lijn.
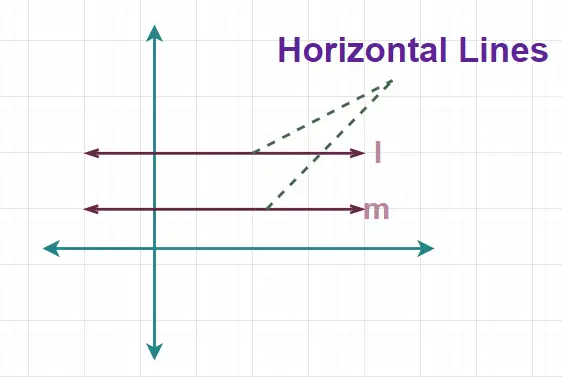
Hier, in de hierboven toegevoegde figuur, zijn de lijnen l en m horizontale lijnen.
Helling van horizontale lijn
We hebben al vermeld dat de helling van de horizontale lijn nul is . Laten we nu eens kijken hoe de helling van de horizontale lijn nul is. We berekenen de helling van een horizontale lijn met behulp van de formule:
Helling = stijgen/rennen
OF
Helling van lijn = verandering in y-coördinaat/verandering in x-coördinaat
mysql-telling
Waar Rise de hoogte is die de lijn wint terwijl hij van links naar rechts loopt, omdat we al weten dat de horizontale lijn evenwijdig is aan de x-as en altijd op een constante hoogte is, zeggen we dat deze lijnen geen stijging hebben, dus de helling van deze lijnen is,
Dus helling = 0/run = 0
Er wordt dus geconcludeerd dat de helling van de horizontale lijn nul is.
Een horizontale lijn tekenen
Horizontale lijnen kunnen eenvoudig worden getekend met behulp van de hieronder besproken stappen.
Stap 1: Neem een punt op het cartesiaanse vlak waarvoor we de horizontale lijn moeten vinden. Stel dat het punt (1, 2) is
Stap 2: Markeert de y-coördinaat van het punt. In dit geval is de y-coördinaat 2.
Stap 3: Markeer andere punten waar de y-coördinaat hetzelfde is als het punt in stap 1. Laat de andere punten (-2, 2), (0, 2) en (7, 2) zijn
Stap 4: Verbind alle punten om een lijnsegment te krijgen en verleng ze aan beide kanten om een horizontale lijn te krijgen.
Dit is de vereiste horizontale lijn die door het punt (1, 2) gaat en een helling van nul heeft.

Horizontale lijnvergelijking
We weten dat de vergelijking van de lijn in het 2D-coördinatensysteem is:
y = mx + c
Waar,
- m is de helling van de lijn
- c is het snijpunt op de y-as
We weten dat voor de horizontale lijn de helling nul is. Door deze waarde in de bovenstaande vergelijking te vervangen, krijgen we de vergelijking van de horizontale lijn:
y = 0x + c
y = c
Waar C is een constante.
De bovenstaande vergelijking y = c is dus de vergelijking van de horizontale lijn.
Deze vergelijking betekent dat de horizontale lijn een lijn is die door alle punten in de cartesiaanse lijn gaat waar de y-coördinaat gelijk is aan ‘c’. Deze lijnsnede heeft geen x-coördinaat en daarom snijdt deze lijn nooit de x-as en snijdt hij de y-as op punt (0, c).
We kunnen dus zeggen dat de vergelijking van de horizontale lijn is: y = c(constant) en deze gaat door het punt (a, c) waar a elke waarde kan aannemen en c altijd constant is.
Horizontale lijntest
Een test die wordt gebruikt om te definiëren of een functie een één-op-één-functie is of niet, is de Horizontale lijntest. Bij de horizontale lijntest tekenen we een horizontale lijn die door een bepaald punt van de functie gaat en als de lijnen de functie op een ander punt doorsnijden, dan is de functie GEEN één-op-één-functie. Om een functie één-op-één te laten zijn, moet deze dus de test voor de horizontale lijn doorstaan, dat wil zeggen dat elke horizontale lijn de functie slechts één keer hoeft te doorbreken.
We weten dat één-op-één-functies de functies zijn waarbij we voor elke waarde van x slechts één waarde van y hebben. Dus als de horizontale lijn door de functie gaat en deze slechts één keer doorsnijdt, kunnen we zeggen dat we voor de unieke waarde van y een unieke waarde van x hebben. Maar als de horizontale lijn de functie meerdere keren doorsnijdt, krijgen we twee waarden voor de unieke waarde van y, wat niet het geval is voor de één-op-één-functie.
Horizontale lijntest helpt ons te bepalen of een functie een één-één-functie is. Dit kan worden begrepen met behulp van de onderstaande afbeelding.

c reeks tekenreeksen
In de eerste afbeelding is de functie één-op-één omdat de horizontale lijn slechts door één punt van de functie gaat.
In de tweede afbeelding is de functie NIET één-op-één, aangezien de horizontale lijn door meer dan één punt van de functie gaat.
Horizontale en verticale lijnen
Horizontale lijnen zijn lijnen die evenwijdig lopen aan de grond of de horizon. Deze lijnen worden ook wel de slaaplijnen genoemd. In het cartesiaanse systeem zijn deze lijnen evenwijdig aan de x-as, terwijl dit voor de verticale lijnen de lijnen zijn die loodrecht op de horizontale lijnen staan, ze worden de staande lijnen genoemd. en zijn evenwijdig aan de y-as in het cartesiaanse systeem.
Horizontale lijnen zijn de lijnen die van links naar rechts lopen in het cartesiaanse systeem, terwijl verticale lijnen de lijnen zijn die op en neer lopen in het cartesiaanse systeem.
Verticale en horizontale lijnen staan loodrecht op elkaar. De onderstaande afbeelding toont een verticale en horizontale lijn.

Verschillen tussen verticale lijnen en horizontale lijnen
De verschillen tussen verticale lijnen en horizontale lijnen kunnen gemakkelijk worden begrepen door de onderstaande tabel te bestuderen.
| Horizontale lijn | Verticale lijn |
|---|---|
| Deze lijnen lopen evenwijdig aan de grond of de horizon. | Deze lijnen zijn loodrecht naar de grond of de horizon. |
| De helling van de horizontale lijn is nul. | De helling van de verticale lijn is niet gedefinieerd. |
| De horizontale lijn maakte een hoek van nul graden met de horizon. | Verticale lijn maakte een hoek van 90 graden met de horizon. |
| Vergelijking van de horizontale lijn die door het punt (h, k) gaat, is: y = k | Vergelijking van de verticale lijn die door het punt (h, k) gaat, is: x = h |
| Horizontale lijnen zijn evenwijdig aan de x-as in het cartesiaanse systeem. | Verticale lijnen zijn evenwijdig aan de y-as in het cartesiaanse systeem. |
| Voorbeelden die de horizontale lijnen vertegenwoordigen zijn:
| Voorbeelden die de verticale lijnen vertegenwoordigen zijn:
|
Korte opmerking over horizontale lijn
Een horizontale lijn in de wiskunde is perfect vlak, evenwijdig aan de horizon. Het loopt van links naar rechts en heeft een helling van 0. In de meetkunde wordt het weergegeven als een rechte lijn die twee willekeurige punten op dezelfde hoogte in een vlak verbindt. De vergelijking voor een horizontale lijn heeft de vorm (y = k), waarbij (k) een constante waarde is die de hoogte van de lijn op de y-as vertegenwoordigt.
Lees verder:
- Soorten lijnen
- Parallelle lijnen
- Hoe voeg ik een horizontale lijn toe in HTML?
- Hoe gebruik ik volledige horizontale regelafstand in HTML?
- Hoe u horizontale en verticale lijnen tekent in een Android-app met behulp van XML
Voorbeelden van horizontale lijnen
Voorbeeld 1: Zoek de vergelijking van de horizontale lijn die door het punt (1, -1) gaat.
Oplossing:
We weten dat de helling van de horizontale lijn m = 0 is.
Gegeven punt (1, -1)
Vergelijking van de lijn die door een punt gaat (x1, En1) en een helling (m) hebben is,
en en1= m(x – x1)
Als we de waarden in de bovenstaande vergelijking vervangen, krijgen we:
y – (-1) = 0(x – 1)
en + 1 = 0
ingesteld in Javay = -1
De vergelijking van de horizontale lijn die door het punt (1, -1) gaat, is dus: y = -1
Voorbeeld 2: Zoek de vergelijking van de horizontale lijn die door het punt (5, 9) gaat.
Oplossing:
We weten dat de helling van de horizontale lijn m = 0 is.
Gegeven punt (5, 9)
Vergelijking van de lijn die door een punt gaat (x1, En1) en een helling (m) hebben is,
en en1= m(x – x1)
Als we de waarden in de bovenstaande vergelijking vervangen, krijgen we:
y – (9) = 0(x – 5)
en – 9 = 0
j = 9
De vergelijking van de horizontale lijn die door het punt (5, 9) gaat, is dus: y = 9
shweta tiwari
Voorbeeld 3: Zoek de vergelijking van de horizontale lijn wanneer het y-snijpunt van de lijn 5 is.
Oplossing:
Vergelijking van de horizontale lijn is,
y = k
waar k is y-snijpunt
Gegeven
- k = 5
Vergelijking van de horizontale lijn,
j = 5
Dus de vergelijking horizontale lijn met y-snijpunt als 5 is, y = 5
Voorbeeld 4: Zoek de vergelijking van de horizontale lijn wanneer het y-snijpunt van de lijn -11/3 is.
Oplossing:
Vergelijking van de horizontale lijn is,
y = k
waar k is y-snijpunt
Gegeven
- k = -11/3
Vergelijking van de horizontale lijn,
y = -11/3
3j = -11
3j + 11 = 0
De vergelijking horizontale lijn met y-snijpunt als -11/3 is dus: 3y + 11 = 0
Horizontale lijnen – Veelgestelde vragen
Wat zijn horizontale lijnen?
Horizontale lijnen zijn lijnen die evenwijdig lopen aan de horizon of de grond. In het cartesiaanse systeem zijn horizontale lijnen evenwijdig aan de x-as.
Wat is de vergelijking van de horizontale lijn?
Vergelijking van de horizontale lijn is,
y = k
waar k is het snijpunt op de y-as.
Wat is de helling van een horizontale lijn?
De helling van de horizontale lijn is altijd gelijk aan nul, omdat deze een hoek van nul graden maakt met de x-as.
Wat zijn voorbeelden van horizontale lijnen?
Voorbeelden die de horizontale lijnen vertegenwoordigen zijn:
- Rechte weg
- Onderkant van trap
- Basis van elk figuur, enz.
Hoe worden de horizontale lijnen op de wereldbol genoemd?
Horizontale lijnen die over de aardbol lopen, worden breedtegraden genoemd en lopen parallel aan de evenaar.
Wat zijn de eigenschappen van horizontale lijnen?
Verschillende eigenschappen van de horizontale lijnen zijn,
Java Lambda-expressies
- Ze zijn evenwijdig aan de grond, de horizon en de x-as.
- Ze staan loodrecht op de y-as.
- De helling van de horizontale lijn is nul, enz.
Welke lijn is verticaal en horizontaal?
Een verticale lijn is evenwijdig aan de y-as en loopt recht op en neer in een coördinatenvlak, terwijl een horizontale lijn evenwijdig is aan de x-as en recht naar links en rechts loopt.
Wat is de helling van een horizontale en verticale lijn?
De helling van een lijn geeft de steilheid en richting aan. Het wordt berekend als de verhouding tussen de verticale verandering en de horizontale verandering tussen twee punten op de lijn.
Wat zijn de horizontale en verticale puntlijnen?
Horizontale lijnen strekken zich uit van links naar rechts of van rechts naar links en lopen parallel aan de x-as, terwijl verticale lijnen zich op en neer uitstrekken en parallel lopen aan de y-as. Deze twee soorten lijnen staan loodrecht op elkaar.
