Wat is gegevensstructuur:
Een datastructuur is een opslag die wordt gebruikt om gegevens op te slaan en te organiseren. Het is een manier om gegevens op een computer te ordenen, zodat deze efficiënt kunnen worden geopend en bijgewerkt.
Een datastructuur wordt niet alleen gebruikt voor het ordenen van de gegevens. Het wordt ook gebruikt voor het verwerken, ophalen en opslaan van gegevens. In vrijwel elk ontwikkeld programma of softwaresysteem worden verschillende basis- en geavanceerde typen datastructuren gebruikt. We moeten dus een goede kennis hebben van datastructuren.
Data structuren zijn een integraal onderdeel van computers die worden gebruikt voor de rangschikking van gegevens in het geheugen. Ze zijn essentieel en verantwoordelijk voor het efficiënt organiseren, verwerken, openen en opslaan van gegevens. Maar dit is niet alles. Verschillende soorten datastructuren hebben hun kenmerken, kenmerken, toepassingen, voordelen en nadelen. Dus hoe identificeer je een datastructuur die geschikt is voor een bepaalde taak? Wat wordt bedoeld met de term ‘datastructuur’? Hoeveel soorten datastructuren zijn er en waarvoor worden ze gebruikt?

Wat is gegevensstructuur: typen, classificaties en toepassingen
Wij hebben u gedekt. We hebben een volledige lijst gemaakt van alles over wat datastructuur is, wat de soorten datastructuren zijn, de classificatie van datastructuren, de toepassingen van elke datastructuur, enzovoort. In dit artikel bespreken we elk aspect van elke datastructuur, zodat u binnen enkele minuten de beste kunt kiezen.
Inhoudsopgave
- Wat is datastructuur?
- Hoe varieert de datastructuur per datatype?
- Classificatie van gegevensstructuur
- Arrays
- Gekoppelde lijst
- Stapel
- Wachtrij
- Boom
- Grafiek
- Conclusie
Hoe de gegevensstructuur varieert per gegevenstype:
We hebben al geleerd over de datastructuur. Wat er vaak gebeurt, is dat mensen in de war raken tussen datatype en datastructuur. Laten we dus een paar verschillen bekijken tussen gegevenstype en gegevensstructuur om het duidelijk te maken.
| Data type | Data structuur |
|---|---|
| Het datatype is de vorm van een variabele waaraan een waarde kan worden toegekend. Het definieert dat de specifieke variabele alleen de waarden van het gegeven gegevenstype zal toewijzen. | Datastructuur is een verzameling van verschillende soorten gegevens. Die volledige gegevens kunnen worden weergegeven met behulp van een object en kunnen in het hele programma worden gebruikt. |
| Het kan waarde bevatten, maar geen gegevens. Daarom is het gegevensloos. | Het kan meerdere soorten gegevens binnen één object bevatten. |
| De implementatie van een gegevenstype staat bekend als abstracte implementatie. een datum formatteren in Java | Implementatie van de datastructuur staat bekend als concrete implementatie. |
| Er is geen tijdscomplexiteit in het geval van gegevenstypen. | Bij datastructuurobjecten speelt tijdscomplexiteit een belangrijke rol. |
| Bij datatypen wordt de waarde van data niet opgeslagen, omdat deze alleen het type data vertegenwoordigt dat kan worden opgeslagen. | Terwijl in het geval van datastructuren de gegevens en de waarde ervan de ruimte in het hoofdgeheugen van de computer verwerven. Ook kan een datastructuur verschillende soorten en typen gegevens binnen één enkel object bevatten. |
| Voorbeelden van gegevenstypen zijn int, float, double, etc. json van Java-object | Voorbeelden van gegevensstructuren zijn stapel, wachtrij, boom, enz. |
Classificatie van gegevensstructuur:
Datastructuur heeft veel verschillende toepassingen in ons dagelijks leven. Er zijn veel verschillende datastructuren die worden gebruikt om verschillende wiskundige en logische problemen op te lossen. Door gebruik te maken van een datastructuur kan men in relatief korte tijd een zeer grote hoeveelheid gegevens ordenen en verwerken. Laten we eens kijken naar verschillende datastructuren die in verschillende situaties worden gebruikt.
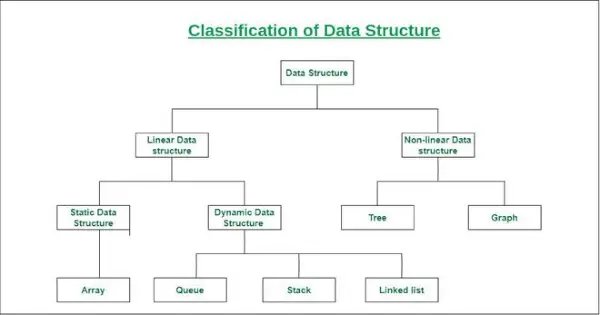
Classificatie van gegevensstructuur
- Lineaire datastructuur: Een datastructuur waarin data-elementen opeenvolgend of lineair zijn gerangschikt, waarbij elk element is gekoppeld aan de vorige en volgende aangrenzende elementen, wordt een lineaire datastructuur genoemd.
Voorbeelden van lineaire datastructuren zijn array, stack, wachtrij, gekoppelde lijst, enz.- Statische datastructuur: Statische datastructuur heeft een vaste geheugengrootte. Het is gemakkelijker om toegang te krijgen tot de elementen in een statische datastructuur.
Een voorbeeld van deze datastructuur is een array. - Dynamische datastructuur: In de dynamische datastructuur staat de grootte niet vast. Het kan willekeurig worden bijgewerkt tijdens de looptijd, wat als efficiënt kan worden beschouwd met betrekking tot de geheugen(ruimte)complexiteit van de code.
Voorbeelden van deze datastructuur zijn wachtrij, stapel, enz.
- Statische datastructuur: Statische datastructuur heeft een vaste geheugengrootte. Het is gemakkelijker om toegang te krijgen tot de elementen in een statische datastructuur.
- Niet-lineaire datastructuur: Datastructuren waarbij data-elementen niet opeenvolgend of lineair worden geplaatst, worden niet-lineaire datastructuren genoemd. In een niet-lineaire datastructuur kunnen we niet alle elementen in één keer doorlopen.
Voorbeelden van niet-lineaire datastructuren zijn bomen en grafieken.
Behoefte aan gegevensstructuur:
De structuur van de data en de synthese van het algoritme zijn relatief ten opzichte van elkaar. De gegevenspresentatie moet gemakkelijk te begrijpen zijn, zodat zowel de ontwikkelaar als de gebruiker de bewerking efficiënt kunnen implementeren.
Datastructuren bieden een eenvoudige manier om gegevens te organiseren, op te halen, te beheren en op te slaan.
Hier is een lijst met de behoeften aan gegevens.
- Het wijzigen van de datastructuur is eenvoudig.
- Het vergt minder tijd.
- Bespaar opslaggeheugenruimte.
- Gegevensrepresentatie is eenvoudig.
- Gemakkelijke toegang tot de grote database.
Arrays:
Een array is een lineaire gegevensstructuur en het is een verzameling items die zijn opgeslagen op aangrenzende geheugenlocaties. Het idee is om meerdere items van hetzelfde type bij elkaar op één plek op te slaan. Het maakt het mogelijk om in relatief korte tijd een grote hoeveelheid gegevens te verwerken. Het eerste element van de array wordt geïndexeerd door een subscript van 0. Er zijn verschillende bewerkingen mogelijk in een array, zoals zoeken, sorteren, invoegen, doorlopen, omkeren en verwijderen.

Array
Kenmerken van een array:
Een array heeft verschillende kenmerken, namelijk:
- Arrays gebruiken een op index gebaseerde gegevensstructuur waarmee elk element in een array gemakkelijk kan worden geïdentificeerd met behulp van de index.
- Als een gebruiker meerdere waarden van hetzelfde gegevenstype wil opslaan, kan de array efficiënt worden gebruikt.
- Een array kan ook complexe datastructuren verwerken door gegevens op te slaan in een tweedimensionale array.
- Een array wordt ook gebruikt om andere datastructuren te implementeren, zoals stapels, wachtrijen, heaps, hashtabellen, enz.
- Het zoekproces in een array kan heel eenvoudig worden uitgevoerd.
Bewerkingen uitgevoerd op array:
- Initialisatie : Een array kan worden geïnitialiseerd met waarden op het moment van declaratie of later met behulp van een toewijzingsinstructie.
- Toegang tot elementen: Elementen in een array zijn toegankelijk via hun index, die begint bij 0 en oploopt tot de grootte van de array min één.
- Zoeken naar elementen : Arrays kunnen worden doorzocht op een specifiek element met behulp van lineaire zoek- of binaire zoekalgoritmen.
- Elementen sorteren : Elementen in een array kunnen in oplopende of aflopende volgorde worden gesorteerd met behulp van algoritmen zoals bellensortering, invoegsortering of snelle sortering.
- Elementen invoegen: Elementen kunnen op een specifieke locatie in een array worden ingevoegd, maar deze bewerking kan tijdrovend zijn omdat hiervoor bestaande elementen in de array moeten worden verschoven.
- Elementen verwijderen: Elementen kunnen uit een array worden verwijderd door de elementen die erna komen te verschuiven om het gat op te vullen.
- Elementen bijwerken: Elementen in een array kunnen worden bijgewerkt of gewijzigd door een nieuwe waarde aan een specifieke index toe te wijzen.
- Doorkruisende elementen: De elementen in een array kunnen in volgorde worden doorlopen, waarbij elk element één keer wordt bezocht.
Dit zijn enkele van de meest voorkomende bewerkingen die op arrays worden uitgevoerd. De specifieke gebruikte bewerkingen en algoritmen kunnen variëren, afhankelijk van de vereisten van het probleem en de gebruikte programmeertaal.
Toepassingen van serie:
Verschillende toepassingen van een array zijn als volgt:
- Een array wordt gebruikt bij het oplossen van matrixproblemen.
- Databaserecords worden ook geïmplementeerd door een array.
- Het helpt bij het implementeren van een sorteeralgoritme.
- Het wordt ook gebruikt om andere datastructuren te implementeren, zoals stapels, wachtrijen, heaps, hashtabellen, enz.
- Een array kan worden gebruikt voor CPU-planning.
- Kan worden toegepast als opzoektabel op computers.
- Arrays kunnen worden gebruikt bij spraakverwerking waarbij elk spraaksignaal een array is.
- Het scherm van de computer wordt ook weergegeven door een array. Hier gebruiken we een multidimensionale array.
- De array wordt gebruikt in veel managementsystemen zoals een bibliotheek, studenten, parlement, enz.
- De array wordt gebruikt in het online ticketboekingssysteem. Contacten op een mobiele telefoon worden door deze array weergegeven.
- In spellen zoals online schaken, waar de speler zowel zijn zetten uit het verleden als zijn huidige zetten kan opslaan. Het geeft een hint van positie aan.
- Om afbeeldingen in een specifieke dimensie op te slaan in de Android Like 360*1200
Real-life toepassingen van Array:
- Een array wordt vaak gebruikt om gegevens op te slaan voor wiskundige berekeningen.
- Het wordt gebruikt bij beeldverwerking.
- Het wordt ook gebruikt bij recordbeheer.
- Boekpagina's zijn ook voorbeelden uit de praktijk van een array.
- Het wordt ook gebruikt bij het bestellen van dozen.
Wil je aan de slag met arrays? U kunt onze samengestelde artikelen en lijsten uitproberen voor de beste praktijken:
- Inleiding tot de arraygegevensstructuur
- Top 50 arraycoderingsproblemen voor interviews
- Oefen het Array-probleem op techcodeview.com
Gelinkte lijst:
Een gekoppelde lijst is een lineaire datastructuur waarin elementen niet op aangrenzende geheugenlocaties worden opgeslagen. De elementen in een gekoppelde lijst zijn gekoppeld met behulp van verwijzingen, zoals weergegeven in de onderstaande afbeelding:
Soorten gekoppelde lijsten:
- Enkelvoudig gekoppelde lijst
- Dubbel gelinkte lijst
- Circulair gekoppelde lijst
- Dubbel circulair gelinkte lijst

Gekoppelde lijst
Kenmerken van een gekoppelde lijst:
Een gekoppelde lijst heeft verschillende kenmerken, namelijk:
- Een gekoppelde lijst gebruikt extra geheugen om koppelingen op te slaan.
- Tijdens de initialisatie van de gekoppelde lijst hoeft u de grootte van de elementen niet te kennen.
- Gekoppelde lijsten worden gebruikt om stapels, wachtrijen, grafieken, enz. te implementeren.
- Het eerste knooppunt van de gekoppelde lijst wordt de Head genoemd.
- De volgende pointer van het laatste knooppunt wijst altijd naar NULL.
- In een gekoppelde lijst is invoegen en verwijderen eenvoudig mogelijk.
- Elk knooppunt van de gekoppelde lijst bestaat uit een pointer/link die het adres is van het volgende knooppunt.
- Gelinkte lijsten kunnen op elk moment gemakkelijk kleiner of groter worden.
Bewerkingen uitgevoerd op de gekoppelde lijst:
Een gekoppelde lijst is een lineaire gegevensstructuur waarbij elk knooppunt een waarde en een verwijzing naar het volgende knooppunt bevat. Hier volgen enkele veelvoorkomende bewerkingen die worden uitgevoerd op gekoppelde lijsten:
- Initialisatie: Een gekoppelde lijst kan worden geïnitialiseerd door een hoofdknooppunt te maken met een verwijzing naar het eerste knooppunt. Elk volgend knooppunt bevat een waarde en een verwijzing naar het volgende knooppunt.
- Elementen invoegen: Elementen kunnen aan de kop, de staart of op een specifieke positie in de gekoppelde lijst worden ingevoegd.
- Elementen verwijderen : Elementen kunnen uit de gekoppelde lijst worden verwijderd door de referentie van het vorige knooppunt bij te werken zodat deze naar het volgende knooppunt verwijst, waardoor het huidige knooppunt effectief uit de lijst wordt verwijderd.
- Zoeken naar elementen : Gekoppelde lijsten kunnen worden doorzocht op een specifiek element door te beginnen bij het hoofdknooppunt en de verwijzingen naar de volgende knooppunten te volgen totdat het gewenste element is gevonden.
- Elementen bijwerken : Elementen in een gekoppelde lijst kunnen worden bijgewerkt door de waarde van een specifiek knooppunt te wijzigen.
- Doorkruisende elementen: De elementen in een gekoppelde lijst kunnen worden doorlopen door te beginnen bij het hoofdknooppunt en de verwijzingen naar de volgende knooppunten te volgen totdat het einde van de lijst is bereikt.
- Een gekoppelde lijst omkeren : De gekoppelde lijst kan worden omgekeerd door de referenties van elk knooppunt bij te werken, zodat ze naar het vorige knooppunt verwijzen in plaats van naar het volgende knooppunt.
Dit zijn enkele van de meest voorkomende bewerkingen die worden uitgevoerd op gekoppelde lijsten. De specifieke gebruikte bewerkingen en algoritmen kunnen variëren, afhankelijk van de vereisten van het probleem en de gebruikte programmeertaal.
Toepassingen van de gekoppelde lijst:
Verschillende toepassingen van gekoppelde lijsten zijn als volgt:
- Gekoppelde lijsten worden gebruikt om stapels, wachtrijen, grafieken, enz. te implementeren.
- Gekoppelde lijsten worden gebruikt om rekenkundige bewerkingen uit te voeren op lange gehele getallen.
- Het wordt gebruikt voor de weergave van schaarse matrices.
- Het wordt gebruikt bij de gekoppelde toewijzing van bestanden.
- Het helpt bij geheugenbeheer.
- Het wordt gebruikt bij de weergave van polynomiale manipulatie, waarbij elke polynomiale term een knooppunt in de gekoppelde lijst vertegenwoordigt.
- Gekoppelde lijsten worden gebruikt om afbeeldingscontainers weer te geven. Gebruikers kunnen eerdere, huidige en volgende afbeeldingen bezoeken.
- Ze worden gebruikt om de geschiedenis van de bezochte pagina op te slaan.
- Ze worden gebruikt om ongedaan gemaakte bewerkingen uit te voeren.
- Linked wordt gebruikt bij de ontwikkeling van software, waarbij ze de juiste syntaxis van een tag aangeven.
- Gekoppelde lijsten worden gebruikt om feeds van sociale media weer te geven.
Real-Life toepassingen van een gekoppelde lijst:
- Bij Round-Robin-planning wordt een gekoppelde lijst gebruikt om de beurt in multiplayer-spellen bij te houden.
- Het wordt gebruikt in de afbeeldingsviewer. De vorige en volgende afbeeldingen zijn met elkaar verbonden en zijn daarom toegankelijk via de vorige en volgende knoppen.
- In een muziekafspeellijst zijn nummers gekoppeld aan het vorige en volgende nummer.
Wilt u aan de slag met een gekoppelde lijst? U kunt onze samengestelde artikelen en lijsten uitproberen voor de beste praktijken:
- Inleiding tot de gegevensstructuur van gekoppelde lijsten
- Top 20 gekoppelde lijst interviewvragen
- Oefen het probleem met de gekoppelde lijst op techcodeview.com
Stapel:
Stack is een lineaire datastructuur die een bepaalde volgorde volgt waarin de bewerkingen worden uitgevoerd. De volgorde is LIFO (Laatste in, eerst uit) . Het invoeren en ophalen van gegevens is slechts vanaf één kant mogelijk. Het invoeren en ophalen van gegevens wordt ook wel push- en pop-operatie in een stapel genoemd. Er zijn verschillende bewerkingen mogelijk in een stapel, zoals het omkeren van een stapel met behulp van recursie, sorteren, het verwijderen van het middelste element van een stapel, enz.

Stapel
Kenmerken van een stapel:
Stack heeft verschillende kenmerken, namelijk:
- Stack wordt gebruikt in veel verschillende algoritmen, zoals de Toren van Hanoi, het doorkruisen van bomen, recursie, enz.
- Stack wordt geïmplementeerd via een array of gekoppelde lijst.
- Het volgt de Last In First Out-bewerking, d.w.z. een element dat als eerste wordt ingevoegd, komt als laatste binnen en omgekeerd.
- Het invoegen en verwijderen wordt aan één uiteinde uitgevoerd, d.w.z. vanaf de bovenkant van de stapel.
- Als in de stapel de toegewezen ruimte voor de stapel vol is en iemand nog steeds probeert meer elementen toe te voegen, zal dit leiden tot een stapeloverloop.
Toepassingen van stapel:
Verschillende toepassingen van Stack zijn als volgt:
- De stapelgegevensstructuur wordt gebruikt bij de evaluatie en conversie van rekenkundige uitdrukkingen.
- Het wordt gebruikt voor het controleren van haakjes.
- Bij het omkeren van een string wordt ook de stapel gebruikt.
- Stack wordt gebruikt bij geheugenbeheer.
- Het wordt ook gebruikt voor het verwerken van functieaanroepen.
- De stapel wordt gebruikt om expressies van infix naar postfix te converteren.
- De stapel wordt gebruikt om zowel ongedaan- als opnieuw-bewerkingen in tekstverwerkers uit te voeren.
- De stapel wordt gebruikt in virtuele machines zoals JVM.
- De stapel wordt gebruikt in de mediaspelers. Handig om het volgende en vorige nummer af te spelen.
- De stapel wordt gebruikt bij recursiebewerkingen.
Bewerking uitgevoerd op stapel;
Een stapel is een lineaire datastructuur die het Last-In-First-Out (LIFO)-principe implementeert. Hier volgen enkele veelvoorkomende bewerkingen die op stapels worden uitgevoerd:
- Duw : Elementen kunnen bovenop de stapel worden geduwd, waardoor een nieuw element bovenaan de stapel wordt toegevoegd.
- Knal : Het bovenste element kan van de stapel worden verwijderd door een pop-operatie uit te voeren, waardoor effectief het laatste element wordt verwijderd dat op de stapel is geduwd.
- Kijkje: Het bovenste element kan worden geïnspecteerd zonder het van de stapel te verwijderen door middel van een kijkoperatie.
- Is leeg : Er kan worden gecontroleerd of de stapel leeg is.
- Maat : Het aantal elementen in de stapel kan worden bepaald met behulp van een groottebewerking.
Dit zijn enkele van de meest voorkomende bewerkingen die op stapels worden uitgevoerd. De specifieke gebruikte bewerkingen en algoritmen kunnen variëren, afhankelijk van de vereisten van het probleem en de gebruikte programmeertaal. Stapels worden vaak gebruikt in toepassingen zoals het evalueren van uitdrukkingen, het implementeren van functieaanroepstapels in computerprogramma's en vele andere.
Real-life toepassingen van Stack:
- Een voorbeeld uit de praktijk van een stapel is de laag eetborden die boven elkaar zijn geplaatst. Wanneer u een bord van de stapel verwijdert, kunt u het bord naar de bovenkant van de stapel brengen. Maar dit is precies de plaat die het laatst op de stapel is gelegd. Als je de plaat onderaan de stapel wilt hebben, moet je alle platen erboven verwijderen om erbij te kunnen.
- Browsers gebruiken stapelgegevensstructuren om eerder bezochte sites bij te houden.
- Oproeplog in mobiel maakt ook gebruik van de stapelgegevensstructuur.
Wil je aan de slag met Stack? U kunt onze samengestelde artikelen en lijsten uitproberen voor de beste praktijken:
np.nullen
- Oefen het stapelprobleem op techcodeview.com
Wachtrij:
Wachtrij is een lineaire gegevensstructuur die een bepaalde volgorde volgt waarin de bewerkingen worden uitgevoerd. De volgorde is Eerst in, eerst uit (FIFO) d.w.z. het als eerste opgeslagen gegevensitem zal als eerste worden benaderd. Hierbij gebeurt het invoeren en ophalen van gegevens niet slechts vanaf één kant. Een voorbeeld van een wachtrij is een rij consumenten voor een hulpbron waarbij de consument die het eerst kwam, als eerste wordt bediend. Er worden verschillende bewerkingen uitgevoerd op een wachtrij, zoals het omkeren van een wachtrij (met of zonder gebruik van recursie), het omkeren van de eerste K-elementen van een wachtrij, enz. Een paar basisbewerkingen die in de wachtrij worden uitgevoerd zijn in de wachtrij plaatsen, uit de wachtrij halen, vooraan, achteraan, enz.
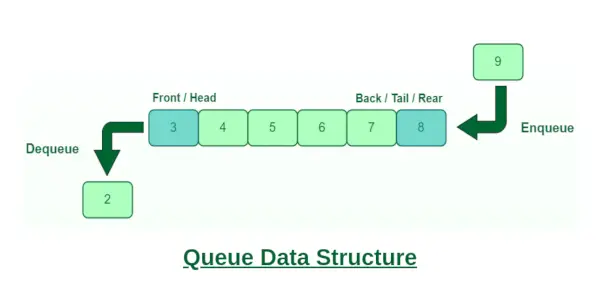
Wachtrij
Kenmerken van een wachtrij:
De wachtrij heeft verschillende kenmerken, namelijk:
- De wachtrij is een FIFO-structuur (First In First Out).
- Om het laatste element van de wachtrij te verwijderen, moeten alle elementen die vóór het nieuwe element in de wachtrij zijn ingevoegd, worden verwijderd.
- Een wachtrij is een geordende lijst met elementen van vergelijkbare gegevenstypen.
Toepassingen van wachtrij:
Verschillende toepassingen van Queue zijn als volgt:
- Wachtrij wordt gebruikt voor het afhandelen van websiteverkeer.
- Het helpt om de afspeellijst in mediaspelers te behouden.
- Wachtrij wordt in besturingssystemen gebruikt voor het afhandelen van interrupts.
- Het helpt bij het verwerken van verzoeken op een enkele gedeelde bron, zoals een printer, CPU-taakplanning, enz.
- Het wordt gebruikt bij de asynchrone overdracht van gegevens, b.v. pijpen, bestands-IO en sockets.
- Wachtrijen worden gebruikt voor taakplanning in het besturingssysteem.
- Op sociale media wordt voor het uploaden van meerdere foto's of video's een wachtrij gebruikt.
- Voor het verzenden van een e-mailwachtrij wordt gebruik gemaakt van de datastructuur.
- Om het websiteverkeer in één keer af te handelen, worden wachtrijen gebruikt.
- In Windows-besturingssysteem, om tussen meerdere applicaties te schakelen.
Bewerking uitgevoerd in wachtrij:
Een wachtrij is een lineaire gegevensstructuur die het First-In-First-Out (FIFO)-principe implementeert. Hier volgen enkele veelvoorkomende bewerkingen die op wachtrijen worden uitgevoerd:
- In de wachtrij plaatsen : Elementen kunnen achteraan de wachtrij worden toegevoegd, waardoor een nieuw element aan het einde van de wachtrij wordt toegevoegd.
- Overeenkomstig : Het voorste element kan uit de wachtrij worden verwijderd door een dequeue-bewerking uit te voeren, waarbij effectief het eerste element wordt verwijderd dat aan de wachtrij is toegevoegd.
- Kijkje : Het frontelement kan worden geïnspecteerd zonder het uit de wachtrij te verwijderen door middel van een kijkoperatie.
- Is leeg : Er kan worden gecontroleerd of de wachtrij leeg is.
- Maat : Het aantal elementen in de wachtrij kan worden bepaald met behulp van een groottebewerking.
Dit zijn enkele van de meest voorkomende bewerkingen die op wachtrijen worden uitgevoerd. De specifieke gebruikte bewerkingen en algoritmen kunnen variëren, afhankelijk van de vereisten van het probleem en de gebruikte programmeertaal. Wachtrijen worden vaak gebruikt in toepassingen zoals het plannen van taken, het beheren van de communicatie tussen processen en vele andere.
Real-life toepassingen van wachtrij:
- Een praktijkvoorbeeld van een wachtrij is een eenrichtingsweg met één rijstrook, waarbij het voertuig dat als eerste binnenkomt, als eerste vertrekt.
- Een realistischer voorbeeld is te zien in de rij bij de loketten.
- Een kassalijn in een winkel is ook een voorbeeld van een wachtrij.
- Mensen op een roltrap
Wil je aan de slag met Queue? U kunt onze samengestelde artikelen en lijsten uitproberen voor de beste praktijken:
- Oefenwachtrijprobleem op techcodeview.com
Boom:
Een boom is een niet-lineaire en hiërarchische gegevensstructuur waarbij de elementen in een boomachtige structuur zijn gerangschikt. In een boom wordt het bovenste knooppunt het hoofdknooppunt genoemd. Elk knooppunt bevat een aantal gegevens en gegevens kunnen van elk type zijn. Het bestaat uit een centraal knooppunt, structurele knooppunten en subknooppunten die via randen zijn verbonden. Verschillende boomdatastructuren maken een snellere en gemakkelijkere toegang tot de gegevens mogelijk, omdat het een niet-lineaire datastructuur is. Een boom heeft verschillende terminologieën zoals knooppunt, wortel, rand, hoogte van een boom, graad van een boom, enz.
Er zijn verschillende soorten Boomachtigen
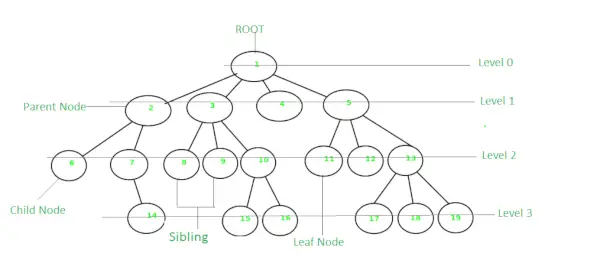
Boom
Kenmerken van een boom:
De boom heeft verschillende kenmerken, namelijk:
- Een boom wordt ook wel een recursieve datastructuur genoemd.
- In een boom kan de Hoogte van de wortel worden gedefinieerd als het langste pad van het wortelknooppunt naar het bladknooppunt.
- In een boom kan men ook de diepte berekenen vanaf de bovenkant tot elk knooppunt. Het wortelknooppunt heeft een diepte van 0.
Toepassingen van boom:
Verschillende toepassingen van Tree zijn als volgt:
- Heap is een boomgegevensstructuur die wordt geïmplementeerd met behulp van arrays en wordt gebruikt om prioriteitswachtrijen te implementeren.
- B-Tree en B+ Tree worden gebruikt om indexering in databases te implementeren.
- Syntax Tree helpt bij het scannen, parseren, genereren van code en evalueren van rekenkundige expressies in het ontwerp van Compiler.
- K-D Tree is een ruimtepartitioneringsboom die wordt gebruikt om punten in de K-dimensionale ruimte te ordenen.
- Spanningsbomen worden gebruikt in routers in computernetwerken.
Bewerking uitgevoerd op boom:
Een boom is een niet-lineaire gegevensstructuur die bestaat uit knooppunten die met elkaar zijn verbonden door randen. Hier volgen enkele veelvoorkomende bewerkingen op bomen:
- Plaatsing : Nieuwe knooppunten kunnen aan de boom worden toegevoegd om een nieuwe tak te creëren of om de hoogte van de boom te vergroten.
- Verwijdering : Knooppunten kunnen uit de boom worden verwijderd door de referenties van het bovenliggende knooppunt bij te werken om de verwijzing naar het huidige knooppunt te verwijderen.
- Zoekopdracht : Er kan naar elementen in een boom worden gezocht door te beginnen bij het hoofdknooppunt en de boom te doorkruisen op basis van de waarde van het huidige knooppunt totdat het gewenste knooppunt is gevonden.
- Traversaal : De elementen in een boom kunnen op verschillende manieren worden doorlopen, waaronder in volgorde, vóór de bestelling en na de bestelling.
- Hoogte : De hoogte van de boom kan worden bepaald door het aantal randen vanaf het wortelknooppunt tot het verste bladknooppunt te tellen.
- Diepte : De diepte van een knooppunt kan worden bepaald door het aantal randen vanaf het hoofdknooppunt tot het huidige knooppunt te tellen.
- Balanceren : De boom kan uitgebalanceerd worden om ervoor te zorgen dat de hoogte van de boom geminimaliseerd wordt en de verdeling van de knooppunten zo gelijkmatig mogelijk is.
Dit zijn enkele van de meest voorkomende bewerkingen die aan bomen worden uitgevoerd. De specifieke gebruikte bewerkingen en algoritmen kunnen variëren, afhankelijk van de vereisten van het probleem en de gebruikte programmeertaal. Bomen worden vaak gebruikt in toepassingen zoals het zoeken, sorteren en opslaan van hiërarchische gegevens.
Real-life toepassingen van Tree:
- In het echte leven helpt de boomdatastructuur bij de ontwikkeling van games.
- Het helpt ook bij het indexeren in databases.
- Een beslissingsboom is een efficiënt hulpmiddel voor machinaal leren, dat vaak wordt gebruikt bij beslissingsanalyse. Het heeft een stroomdiagramachtige structuur die helpt gegevens te begrijpen.
- Domain Name Server maakt ook gebruik van een boomdatastructuur.
- Het meest voorkomende gebruik van een boom is elke sociale netwerksite.
Wil je aan de slag met Boom? U kunt onze samengestelde artikelen en lijsten uitproberen voor de beste praktijken:
- Top 50 Tree-interviewvragen
- Oefen het Boomprobleem op techcodeview.com
Grafiek:
Een grafiek is een niet-lineaire gegevensstructuur die bestaat uit hoekpunten (of knooppunten) en randen. Het bestaat uit een eindige reeks hoekpunten en een reeks randen die een paar knooppunten verbinden. De grafiek wordt gebruikt om de meest uitdagende en complexe programmeerproblemen op te lossen. Het heeft verschillende terminologieën: pad, graad, aangrenzende hoekpunten, verbonden componenten, enz.
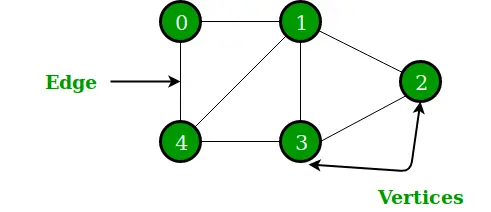
Grafiek
Kenmerken van grafiek:
De grafiek heeft verschillende kenmerken, namelijk:
- De maximale afstand van een hoekpunt tot alle andere hoekpunten wordt beschouwd als de excentriciteit van dat hoekpunt.
- Het hoekpunt met minimale excentriciteit wordt beschouwd als het centrale punt van de grafiek.
- De minimumwaarde van excentriciteit van alle hoekpunten wordt beschouwd als de straal van een verbonden grafiek.
Toepassingen van grafiek:
Verschillende toepassingen van grafieken zijn als volgt:
- De grafiek wordt gebruikt om de stroom van de berekeningen weer te geven.
- Het wordt gebruikt bij het modelleren van grafieken.
- Het besturingssysteem maakt gebruik van Resource Allocation Graph.
- Wordt ook gebruikt op het World Wide Web, waar de webpagina's de knooppunten vertegenwoordigen.
Bewerking uitgevoerd op grafiek:
Een grafiek is een niet-lineaire gegevensstructuur bestaande uit knooppunten en randen. Hier volgen enkele veelvoorkomende bewerkingen die op grafieken worden uitgevoerd:
- Hoekpunt toevoegen: Er kunnen nieuwe hoekpunten aan de grafiek worden toegevoegd om een nieuw knooppunt weer te geven.
- Rand toevoegen: Randen kunnen tussen hoekpunten worden toegevoegd om een relatie tussen knooppunten weer te geven.
- Hoekpunt verwijderen : Hoekpunten kunnen uit de grafiek worden verwijderd door de referenties van aangrenzende hoekpunten bij te werken om de verwijzing naar het huidige hoekpunt te verwijderen.
- Rand verwijderen : Randen kunnen worden verwijderd door de referenties van de aangrenzende hoekpunten bij te werken om de verwijzing naar de huidige rand te verwijderen.
- Diepte-eerst zoeken (DFS) : Een grafiek kan worden doorlopen met behulp van een diepte-eerst-zoekopdracht door de hoekpunten op een diepte-eerst-manier te bezoeken.
- B readth-First Search (BFS): Een grafiek kan worden doorlopen met behulp van een breedte-eerst-zoekopdracht door de hoekpunten eerst in de breedte te bezoeken.
- Kortste weg: Het kortste pad tussen twee hoekpunten kan worden bepaald met behulp van algoritmen zoals het algoritme van Dijkstra of het A*-algoritme.
- Verbonden componenten : De verbonden componenten van een grafiek kunnen worden bepaald door reeksen hoekpunten te vinden die met elkaar zijn verbonden, maar niet met andere hoekpunten in de grafiek.
- Cyclusdetectie : Cycli in een grafiek kunnen worden gedetecteerd door te controleren op achterranden tijdens een diepte-eerst-zoekopdracht.
Dit zijn enkele van de meest voorkomende bewerkingen die op grafieken worden uitgevoerd. De specifieke gebruikte bewerkingen en algoritmen kunnen variëren, afhankelijk van de vereisten van het probleem en de gebruikte programmeertaal. Grafieken worden vaak gebruikt in toepassingen zoals computernetwerken, sociale netwerken en routeringsproblemen.
Real-life toepassingen van Graph:
- Een van de meest voorkomende voorbeelden van een grafiek in de echte wereld is Google Maps, waar steden zich bevinden als hoekpunten en paden die deze hoekpunten verbinden zich bevinden als randen van de grafiek.
- Een sociaal netwerk is ook een voorbeeld uit de praktijk van een grafiek waarin elke persoon op het netwerk een knooppunt is en al hun vriendschappen op het netwerk de randen van de grafiek vormen.
- Een grafiek wordt ook gebruikt om moleculen in de natuur- en scheikunde te bestuderen.
Wil je aan de slag met Grafiek? U kunt onze samengestelde artikelen en lijsten uitproberen voor de beste praktijken:
Ankita Lokhande leeftijd
- Inleiding tot de structuur van grafiekgegevens
- Top 50 grafiek-interviewvragen
- Oefen het grafiekprobleem op techcodeview.com
Voordelen van datastructuur:
- Verbeterde gegevensorganisatie en opslagefficiëntie.
- Sneller ophalen en manipuleren van gegevens.
- Vergemakkelijkt het ontwerp van algoritmen voor het oplossen van complexe problemen.
- Vereenvoudigt de taak van het bijwerken en onderhouden van de gegevens.
- Biedt een beter inzicht in de relaties tussen gegevenselementen.
Nadeel van datastructuur:
- Verhoogde reken- en geheugenoverhead.
- Moeilijkheden bij het ontwerpen en implementeren van complexe datastructuren.
- Beperkte schaalbaarheid en flexibiliteit.
- Complexiteit bij het debuggen en testen.
- Moeilijkheden bij het wijzigen van bestaande datastructuren.
Referentie:
Datastructuren zijn te vinden in verschillende computerwetenschappelijke leerboeken en online bronnen. Enkele populaire teksten zijn onder meer:
- Inleiding tot algoritmen door Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest en Clifford Stein.
- Datastructuren en algoritmeanalyse in Java door Mark Allen Weiss.
- De algoritmeontwerphandleiding door Steven S. Skiena.
- Online bronnen zoals Coursera, Udemy en Khan Academy bieden ook cursussen over datastructuren en algoritmen.
Conclusie
Hoewel dit de meest bekende en gebruikte datastructuren zijn, zijn er ook enkele andere vormen van datastructuren die in de informatica worden gebruikt, zoals beleidsgebaseerde datastructuren , enz. Maar welke datastructuur u ook kiest, elke structuur heeft zijn voor- en nadelen. Zonder de kennis daarvan kan het erg kostbaar zijn om het verkeerde type datastructuur te kiezen. Het is dus erg belangrijk om de noodzaak van de situatie te begrijpen en vervolgens te beslissen welk soort datastructuur het beste bij de taak past.
