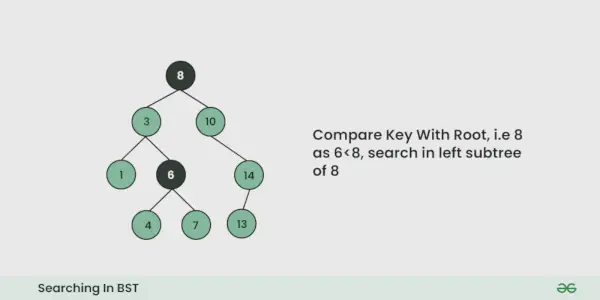
Gegeven een BST , de taak is om hierin een knooppunt te zoeken BST .
Als u een waarde in BST zoekt, beschouw deze dan als een gesorteerde array. Nu kunnen we eenvoudig een zoekbewerking uitvoeren in BST met behulp van Binair zoekalgoritme .
Algoritme om naar een sleutel te zoeken in een bepaalde binaire zoekboom:
Stel dat we naar het nummer willen zoeken X, Wij beginnen bij de wortel. Dan:
- We vergelijken de te zoeken waarde met de waarde van de wortel.
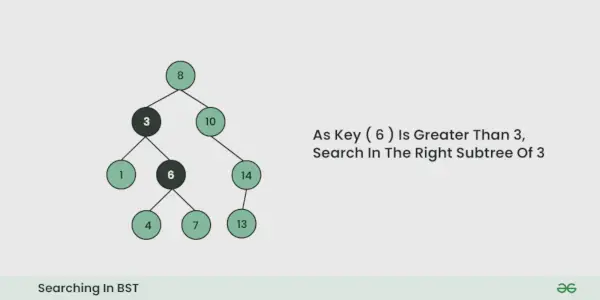
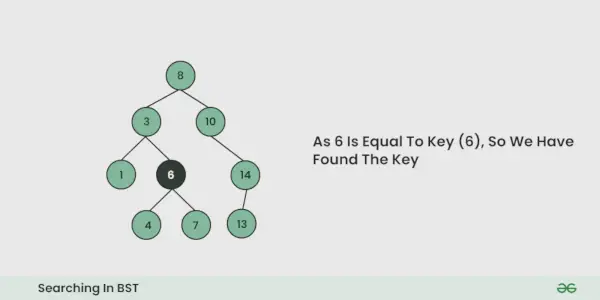
- Als het gelijk is, zijn we klaar met zoeken. Als het kleiner is, weten we dat we naar de linker subboom moeten gaan, omdat in een binaire zoekboom alle elementen in de linker subboom kleiner zijn en alle elementen in de rechter subboom groter zijn.
- Herhaal de bovenstaande stap totdat er geen verplaatsing meer mogelijk is
- Als er bij een iteratie een sleutel wordt gevonden, retourneert u True. Anders vals.
Illustratie van zoeken in een BST:
Zie de onderstaande afbeelding voor een beter begrip:
Aanbevolen praktijkZoek een knooppunt in BSTTProbeer het!
Programma om zoeken in BST te implementeren:
C++
// C++ function to search a given key in a given BST> #include> using> namespace> std;> struct> node {> >int> key;> >struct> node *left, *right;> };> // A utility function to create a new BST node> struct> node* newNode(>int> item)> {> >struct> node* temp> >=>new> struct> node;> >temp->sleutel = item;> >temp->links = temp->rechts = NULL;> >return> temp;> }> // A utility function to insert> // a new node with given key in BST> struct> node* insert(>struct> node* node,>int> key)> {> >// If the tree is empty, return a new node> >if> (node == NULL)> >return> newNode(key);> >// Otherwise, recur down the tree> >if> (key key)> >node->links = invoegen(knooppunt->links, sleutel);> >else> if> (key>knooppunt->sleutel)> >node->rechts = invoegen(knooppunt->rechts, sleutel);> >// Return the (unchanged) node pointer> >return> node;> }> // Utility function to search a key in a BST> struct> node* search(>struct> node* root,>int> key)> > >// Base Cases: root is null or key is present at root> >if> (root == NULL> // Driver Code> int> main()> {> >struct> node* root = NULL;> >root = insert(root, 50);> >insert(root, 30);> >insert(root, 20);> >insert(root, 40);> >insert(root, 70);> >insert(root, 60);> >insert(root, 80);> >// Key to be found> >int> key = 6;> >// Searching in a BST> >if> (search(root, key) == NULL)> >cout << key <<>' not found'> << endl;> >else> >cout << key <<>' found'> << endl;> >key = 60;> >// Searching in a BST> >if> (search(root, key) == NULL)> >cout << key <<>' not found'> << endl;> >else> >cout << key <<>' found'> << endl;> >return> 0;> }> |
>
>
JavaScript-trim-subtekenreeks
C
// C function to search a given key in a given BST> #include> #include> struct> node {> >int> key;> >struct> node *left, *right;> };> // A utility function to create a new BST node> struct> node* newNode(>int> item)> {> >struct> node* temp> >= (>struct> node*)>malloc>(>sizeof>(>struct> node));> >temp->sleutel = item;> >temp->links = temp->rechts = NULL;> >return> temp;> }> // A utility function to insert> // a new node with given key in BST> struct> node* insert(>struct> node* node,>int> key)> {> >// If the tree is empty, return a new node> >if> (node == NULL)> >return> newNode(key);> >// Otherwise, recur down the tree> >if> (key key)> >node->links = invoegen(knooppunt->links, sleutel);> >else> if> (key>knooppunt->sleutel)> >node->rechts = invoegen(knooppunt->rechts, sleutel);> >// Return the (unchanged) node pointer> >return> node;> }> // Utility function to search a key in a BST> struct> node* search(>struct> node* root,>int> key)> > // Driver Code> int> main()> {> >struct> node* root = NULL;> >root = insert(root, 50);> >insert(root, 30);> >insert(root, 20);> >insert(root, 40);> >insert(root, 70);> >insert(root, 60);> >insert(root, 80);> >// Key to be found> >int> key = 6;> >// Searching in a BST> >if> (search(root, key) == NULL)> >printf>(>'%d not found
'>, key);> >else> >printf>(>'%d found
'>, key);> >key = 60;> >// Searching in a BST> >if> (search(root, key) == NULL)> >printf>(>'%d not found
'>, key);> >else> >printf>(>'%d found
'>, key);> >return> 0;> }> |
>
>
Java
// Java program to search a given key in a given BST> class> Node {> >int> key;> >Node left, right;> >public> Node(>int> item) {> >key = item;> >left = right =>null>;> >}> }> class> BinarySearchTree {> >Node root;> >// Constructor> >BinarySearchTree() {> >root =>null>;> >}> >// A utility function to insert> >// a new node with given key in BST> >Node insert(Node node,>int> key) {> >// If the tree is empty, return a new node> >if> (node ==>null>) {> >node =>new> Node(key);> >return> node;> >}> >// Otherwise, recur down the tree> >if> (key node.left = insert(node.left, key); else if (key>knooppunt.sleutel) knooppunt.rechts = invoegen(knooppunt.rechts, sleutel); // Retourneer het (ongewijzigde) knooppunt-pointer-retourknooppunt; } // Hulpprogrammafunctie om een sleutel te zoeken in een BST-knooppuntzoekopdracht (knooppuntroot, int-sleutel) // Stuurprogrammacode public static void main (String [] args) { BinarySearchTree tree = new BinarySearchTree (); // Knooppunten invoegen tree.root = tree.insert(tree.root, 50); boom.insert(boom.root, 30); boom.insert(boom.root, 20); boom.insert(boom.root, 40); boom.insert(boom.root, 70); boom.insert(boom.root, 60); boom.insert(boom.root, 80); // Te vinden sleutel int key = 6; // Zoeken in een BST if (tree.search(tree.root, key) == null) System.out.println(key + 'not found'); anders System.out.println(sleutel + 'gevonden'); sleutel = 60; // Zoeken in een BST if (tree.search(tree.root, key) == null) System.out.println(key + 'not found'); anders System.out.println(sleutel + 'gevonden'); } }> |
>
>
Python3
# Python3 function to search a given key in a given BST> class> Node:> ># Constructor to create a new node> >def> __init__(>self>, key):> >self>.key>=> key> >self>.left>=> None> >self>.right>=> None> # A utility function to insert> # a new node with the given key in BST> def> insert(node, key):> ># If the tree is empty, return a new node> >if> node>is> None>:> >return> Node(key)> ># Otherwise, recur down the tree> >if> key node.left = insert(node.left, key) elif key>node.key: node.right = insert(node.right, key) # Retourneert de (ongewijzigde) knooppuntaanwijzer return node # Hulpprogrammafunctie om een sleutel te zoeken in een BST def-zoekopdracht (root, sleutel): # Basisgevallen: root is null of sleutel is aanwezig in de root als root Geen is of root.key == sleutel: return root # Sleutel is groter dan de sleutel van root als root.key return search(root.right, key) # Sleutel is kleiner dan root 's key return search(root.left, key) # Stuurprogrammacode if __name__ == '__main__': root = Geen root = insert(root, 50) insert(root, 30) insert(root, 20) insert (root, 40) insert(root, 70) insert(root, 60) insert(root, 80) # Te vinden sleutel sleutel = 6 # Zoeken in een BST als zoeken(root, sleutel) Geen is: print(sleutel, 'niet gevonden') else: print(key, 'found') key = 60 # Zoeken in een BST als search(root, key) Geen is: print(key, 'not found') else: print(sleutel, 'gevonden')> |
>
>
C#
// C# function to search a given key in a given BST> using> System;> public> class> Node {> >public> int> key;> >public> Node left, right;> }> public> class> BinaryTree {> >// A utility function to create a new BST node> >public> Node NewNode(>int> item)> >{> >Node temp =>new> Node();> >temp.key = item;> >temp.left = temp.right =>null>;> >return> temp;> >}> >// A utility function to insert> >// a new node with given key in BST> >public> Node Insert(Node node,>int> key)> >{> >// If the tree is empty, return a new node> >if> (node ==>null>)> >return> NewNode(key);> >// Otherwise, recur down the tree> >if> (key node.left = Insert(node.left, key); else if (key>node.key) node.right = Invoegen(node.right, sleutel); // Retourneer het (ongewijzigde) knooppunt-pointer-retourknooppunt; } // Utility-functie om een sleutel te zoeken in een BST public Node Search (Node root, int key) // Basisgevallen: root is null of sleutel is aanwezig in root if (root == null // Driver Code public static void Main () { Knooppuntwortel = nul; BinaryTree bt = nieuwe BinaryTree(); root = bt.Insert(root, 30); , 40); bt.Insert(root, 70); bt.Insert(root, 60); bt.Insert(root, 80); // Te vinden sleutel int sleutel = 6 // Zoeken in een BST if ( bt.Search(root, key) == null) Console.WriteLine(sleutel + 'niet gevonden'); else Console.WriteLine(sleutel + 'gevonden'); if (bt.Search(root, sleutel) == null) Console.WriteLine(sleutel + 'niet gevonden'); else Console.WriteLine(sleutel + 'gevonden'} }> |
>
>
Javascript
// Javascript function to search a given key in a given BST> class Node {> >constructor(key) {> >this>.key = key;> >this>.left =>null>;> >this>.right =>null>;> >}> }> // A utility function to insert> // a new node with given key in BST> function> insert(node, key) {> >// If the tree is empty, return a new node> >if> (node ===>null>) {> >return> new> Node(key);> >}> >// Otherwise, recur down the tree> >if> (key node.left = insert(node.left, key); } else if (key>knooppunt.sleutel) { knooppunt.rechts = invoegen(knooppunt.rechts, sleutel); } // Retourneer het (ongewijzigde) knooppunt-pointer-retourknooppunt; } // Hulpprogramma-functie om een sleutel te zoeken in een BST-functie search(root, key) {// Basisgevallen: root is null of sleutel is aanwezig in root if (root === null || root.key === sleutel ) { retourwortel; } // Sleutel is groter dan root's sleutel if (root.key return search(root.right, key); } // Sleutel is kleiner dan root's key return search(root.left, key); } // Stuurprogrammacode laat root = null; root = insert(root, 50); insert(root, 30); 60); insert(root, 80); // Te vinden sleutel let key = 6; // Zoeken in een BST if (search(root, key) === null) { console.log(key + 'not gevonden'); } else { console.log(sleutel + ' gevonden'); sleutel = 60; // Zoeken in een BST if (search(root, key) === null) { console.log( sleutel + 'niet gevonden'} else { console.log(sleutel + 'gevonden' }>'>). |
>6 not found 60 found>
Tijdcomplexiteit: O(h), waarbij h de hoogte van de BST is.
Hulpruimte: O(h), waarbij h de hoogte van de BST is. Dit komt omdat de maximale hoeveelheid ruimte die nodig is om de recursiestapel op te slaan zou zijn H .
Gerelateerde Links:
- Binaire zoekboom invoegbewerking
- Binaire zoekboomverwijderingsbewerking