De beperkingen van traditionele binaire zoekbomen kunnen frustrerend zijn. Maak kennis met de B-Tree, de veelzijdige datastructuur die met gemak grote hoeveelheden gegevens kan verwerken. Als het gaat om het opslaan en doorzoeken van grote hoeveelheden gegevens, kunnen traditionele binaire zoekbomen onpraktisch worden vanwege hun slechte prestaties en hoog geheugengebruik. B-Trees, ook bekend als B-Tree of Balanced Tree, zijn een soort zelfbalancerende boom die speciaal is ontworpen om deze beperkingen te overwinnen.
In tegenstelling tot traditionele binaire zoekbomen worden B-Trees gekenmerkt door het grote aantal sleutels dat ze in één knooppunt kunnen opslaan. Daarom worden ze ook wel grote sleutelbomen genoemd. Elk knooppunt in een B-Tree kan meerdere sleutels bevatten, waardoor de boom een grotere vertakkingsfactor kan hebben en dus een geringere hoogte. Deze geringe hoogte leidt tot minder schijf-I/O, wat resulteert in snellere zoek- en invoegbewerkingen. B-Trees zijn bijzonder geschikt voor opslagsystemen met trage, omvangrijke gegevenstoegang, zoals harde schijven, flashgeheugen en cd-roms.
B-Trees handhaaft het evenwicht door ervoor te zorgen dat elk knooppunt een minimum aantal sleutels heeft, zodat de boom altijd in evenwicht is. Dit evenwicht garandeert dat de tijdscomplexiteit voor bewerkingen zoals invoegen, verwijderen en zoeken altijd O(log n) is, ongeacht de oorspronkelijke vorm van de boom.
Tijdcomplexiteit van B-Tree:
| Meneer Nee. | Algoritme | Tijdcomplexiteit |
|---|---|---|
| 1. | Zoekopdracht | O(logboek n) |
| 2. | Invoegen | O(logboek n) |
| 3. | Verwijderen | O(logboek n) |
Opmerking: n is het totale aantal elementen in de B-boom
char + int in Java
Eigenschappen van B-Tree:
- Alle bladeren bevinden zich op hetzelfde niveau.
- B-Tree wordt gedefinieerd door de term minimale graad ‘ T ‘. De waarde van ' T ‘ hangt af van de grootte van het schijfblok.
- Elk knooppunt behalve de wortel moet minimaal t-1-sleutels bevatten. De root mag minimaal 1 sleutel.
- Alle knooppunten (inclusief root) mogen maximaal ( 2*t – 1 ) sleutels.
- Het aantal kinderen van een knooppunt is gelijk aan het aantal sleutels erin plus 1 .
- Alle sleutels van een knooppunt worden in oplopende volgorde gesorteerd. Het kind tussen twee sleutels k1 En k2 bevat alle toetsen in het bereik vanaf k1 En k2 .
- B-Tree groeit en krimpt vanaf de wortel, wat anders is dan Binary Search Tree. Binaire zoekbomen groeien naar beneden en krimpen ook naar beneden.
- Net als bij andere gebalanceerde binaire zoekbomen is de tijdscomplexiteit voor het zoeken, invoegen en verwijderen O(log n).
- Het invoegen van een knooppunt in B-Tree gebeurt alleen bij Leaf Node.
Hieronder volgt een voorbeeld van een B-Tree met een minimale bestelling van 5
Opmerking: dat in praktische B-Trees de waarde van de minimale bestelling veel meer dan 5 is.

We kunnen in het bovenstaande diagram zien dat alle bladknooppunten zich op hetzelfde niveau bevinden en dat alle niet-bladknooppunten geen lege subboom hebben en sleutels hebben die één minder zijn dan het aantal van hun kinderen.
Interessante feiten over B-Trees:
- De minimale hoogte van de B-Tree die kan bestaan met n aantal knooppunten en m is het maximale aantal kinderen van een knooppunt dat kan hebben:
- De maximale hoogte van de B-Tree die kan bestaan met n aantal knooppunten en t is het minimale aantal kinderen dat een niet-rootknooppunt kan hebben is:
En
Traversatie in B-boom:
Traversal is ook vergelijkbaar met Inorder-traversal van Binary Tree. We beginnen bij het meest linkse kind, drukken het meest linkse kind recursief af en herhalen vervolgens hetzelfde proces voor de overige kinderen en sleutels. Druk uiteindelijk recursief het meest rechtse kind af.
Zoekoperatie in B-Tree:
Zoeken is vergelijkbaar met zoeken in de binaire zoekboom. Stel dat de sleutel die moet worden doorzocht k is.
- Begin bij de wortel en ga recursief naar beneden.
- Voor elk bezocht niet-bladknooppunt,
- Als het knooppunt de sleutel heeft, retourneren we het knooppunt eenvoudigweg.
- Anders keren we terug naar het juiste kind (het kind dat zich net voor de eerste grotere sleutel bevindt) van het knooppunt.
- Als we een bladknooppunt bereiken en k niet vinden in het bladknooppunt, retourneer dan NULL.
Het zoeken in een B-Tree is vergelijkbaar met het zoeken in een binaire boom. Het algoritme is vergelijkbaar en gaat gepaard met recursie. Op elk niveau wordt de zoekopdracht geoptimaliseerd alsof de sleutelwaarde niet aanwezig is in het bereik van de ouder, maar de sleutel wel aanwezig is in een andere vertakking. Omdat deze waarden de zoekopdracht beperken, worden ze ook wel grenswaarden of scheidingswaarden genoemd. Als we een bladknooppunt bereiken en de gewenste sleutel niet vinden, wordt NULL weergegeven.
Algoritme voor het zoeken naar een element in een B-boom: -
C++
struct> Node {> >int> n;> >int> key[MAX_KEYS];> >Node* child[MAX_CHILDREN];> >bool> leaf;> };> Node* BtreeSearch(Node* x,>int> k) {> >int> i = 0;> >while> (i n && k>x->toets[i]) {> >i++;> >}> >if> (i n && k == x->sleutel[i]) {> >return> x;> >}> >if> (x->blad) {> >return> nullptr;> >}> >return> BtreeSearch(x->kind[i], k);> }> |
>
>
C
BtreeSearch(x, k)> >i = 1> > >// n[x] means number of keys in x node> >while> i ? n[x] and k ? keyi[x]> >do> i = i + 1> >if> i n[x] and k = keyi[x]> >then>return> (x, i)> >if> leaf [x]> >then>return> NIL> >else> >return> BtreeSearch(ci[x], k)> |
>
>
Java
class> Node {> >int> n;> >int>[] key =>new> int>[MAX_KEYS];> >Node[] child =>new> Node[MAX_CHILDREN];> >boolean> leaf;> }> Node BtreeSearch(Node x,>int> k) {> >int> i =>0>;> >while> (i = x.key[i]) {> >i++;> >}> >if> (i return x; } if (x.leaf) { return null; } return BtreeSearch(x.child[i], k); }> |
>
>
Python3
class> Node:> >def> __init__(>self>):> >self>.n>=> 0> >self>.key>=> [>0>]>*> MAX_KEYS> >self>.child>=> [>None>]>*> MAX_CHILDREN> >self>.leaf>=> True> def> BtreeSearch(x, k):> >i>=> 0> >while> i and k>= x.key[i]: i += 1 als i en k == x.key[i]: return x if x.leaf: return Geen return BtreeSearch(x.child[i], k)> |
>
>
C#
class> Node {> >public> int> n;> >public> int>[] key =>new> int>[MAX_KEYS];> >public> Node[] child =>new> Node[MAX_CHILDREN];> >public> bool> leaf;> }> Node BtreeSearch(Node x,>int> k) {> >int> i = 0;> >while> (i = x.key[i]) {> >i++;> >}> >if> (i return x; } if (x.leaf) { return null; } return BtreeSearch(x.child[i], k); }> |
>
>
Javascript
// Define a Node class with properties n, key, child, and leaf> class Node {> >constructor() {> >this>.n = 0;> >this>.key =>new> Array(MAX_KEYS);> >this>.child =>new> Array(MAX_CHILDREN);> >this>.leaf =>false>;> >}> }> // Define a function BtreeSearch that takes in a Node object x and an integer k> function> BtreeSearch(x, k) {> >let i = 0;> >while> (i = x.key[i]) {> >i++;> >}> >if> (i return x; } if (x.leaf) { return null; } return BtreeSearch(x.child[i], k); }> |
>
>
Voorbeelden:
Java initialiseert array
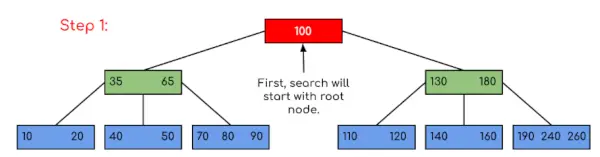
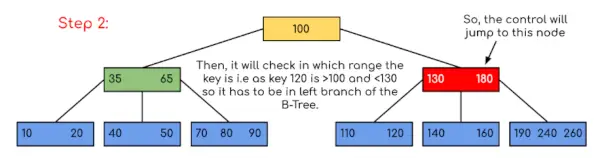
Invoer: Zoek 120 in de gegeven B-Tree.
Oplossing:
Java-pseudocode
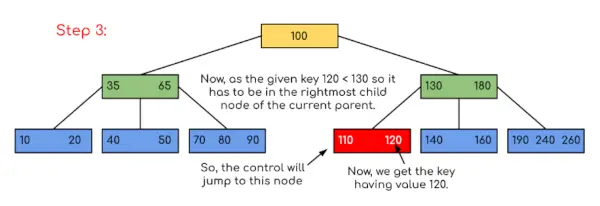
In dit voorbeeld kunnen we zien dat onze zoekopdracht werd verkleind door alleen de kans te beperken dat de sleutel met de waarde aanwezig zou kunnen zijn. Op dezelfde manier, als we in het bovenstaande voorbeeld naar 180 moeten zoeken, stopt de besturing bij stap 2 omdat het programma zal ontdekken dat de sleutel 180 aanwezig is in het huidige knooppunt. En op dezelfde manier, als het 90 moet opzoeken, dan zal het als 90 <100 automatisch naar de linker subboom gaan, en daarom zal de controlestroom op dezelfde manier verlopen als getoond in het bovenstaande voorbeeld.
Hieronder vindt u de implementatie van de bovenstaande aanpak:
C++
// C++ implementation of search() and traverse() methods> #include> using> namespace> std;> // A BTree node> class> BTreeNode {> >int>* keys;>// An array of keys> >int> t;>// Minimum degree (defines the range for number> >// of keys)> >BTreeNode** C;>// An array of child pointers> >int> n;>// Current number of keys> >bool> leaf;>// Is true when node is leaf. Otherwise false> public>:> >BTreeNode(>int> _t,>bool> _leaf);>// Constructor> >// A function to traverse all nodes in a subtree rooted> >// with this node> >void> traverse();> >// A function to search a key in the subtree rooted with> >// this node.> >BTreeNode*> >search(>int> k);>// returns NULL if k is not present.> >// Make the BTree friend of this so that we can access> >// private members of this class in BTree functions> >friend> class> BTree;> };> // A BTree> class> BTree {> >BTreeNode* root;>// Pointer to root node> >int> t;>// Minimum degree> public>:> >// Constructor (Initializes tree as empty)> >BTree(>int> _t)> >{> >root = NULL;> >t = _t;> >}> >// function to traverse the tree> >void> traverse()> >{> >if> (root != NULL)> >root->traverse();> >}> >// function to search a key in this tree> >BTreeNode* search(>int> k)> >{> >return> (root == NULL) ? NULL : root->zoek(k);> >}> };> // Constructor for BTreeNode class> BTreeNode::BTreeNode(>int> _t,>bool> _leaf)> {> >// Copy the given minimum degree and leaf property> >t = _t;> >leaf = _leaf;> >// Allocate memory for maximum number of possible keys> >// and child pointers> >keys =>new> int>[2 * t - 1];> >C =>new> BTreeNode*[2 * t];> >// Initialize the number of keys as 0> >n = 0;> }> // Function to traverse all nodes in a subtree rooted with> // this node> void> BTreeNode::traverse()> {> >// There are n keys and n+1 children, traverse through n> >// keys and first n children> >int> i;> >for> (i = 0; i // If this is not leaf, then before printing key[i], // traverse the subtree rooted with child C[i]. if (leaf == false) C[i]->traverse(); uit<< ' ' << keys[i]; } // Print the subtree rooted with last child if (leaf == false) C[i]->traverse(); } // Functie om sleutel k te zoeken in een subboom die is geroot met dit knooppunt BTreeNode* BTreeNode::search(int k) {// Vind de eerste sleutel groter dan of gelijk aan k int i = 0; terwijl (i toetsen[i]) i++; // Als de gevonden sleutel gelijk is aan k, retourneer dit knooppunt als (keys[i] == k) dit retourneert; // Als de sleutel hier niet wordt gevonden en dit een leaf-knooppunt is, als (leaf == true) NULL retourneert; // Ga naar de juiste subretour C[i]->search(k); }> |
>
>
Java
// Java program to illustrate the sum of two numbers> // A BTree> class> Btree {> >public> BTreeNode root;>// Pointer to root node> >public> int> t;>// Minimum degree> >// Constructor (Initializes tree as empty)> >Btree(>int> t)> >{> >this>.root =>null>;> >this>.t = t;> >}> >// function to traverse the tree> >public> void> traverse()> >{> >if> (>this>.root !=>null>)> >this>.root.traverse();> >System.out.println();> >}> >// function to search a key in this tree> >public> BTreeNode search(>int> k)> >{> >if> (>this>.root ==>null>)> >return> null>;> >else> >return> this>.root.search(k);> >}> }> // A BTree node> class> BTreeNode {> >int>[] keys;>// An array of keys> >int> t;>// Minimum degree (defines the range for number> >// of keys)> >BTreeNode[] C;>// An array of child pointers> >int> n;>// Current number of keys> >boolean> >leaf;>// Is true when node is leaf. Otherwise false> >// Constructor> >BTreeNode(>int> t,>boolean> leaf)> >{> >this>.t = t;> >this>.leaf = leaf;> >this>.keys =>new> int>[>2> * t ->1>];> >this>.C =>new> BTreeNode[>2> * t];> >this>.n =>0>;> >}> >// A function to traverse all nodes in a subtree rooted> >// with this node> >public> void> traverse()> >{> >// There are n keys and n+1 children, traverse> >// through n keys and first n children> >int> i =>0>;> >for> (i =>0>; i <>this>.n; i++) {> >// If this is not leaf, then before printing> >// key[i], traverse the subtree rooted with> >// child C[i].> >if> (>this>.leaf ==>false>) {> >C[i].traverse();> >}> >System.out.print(keys[i] +>' '>);> >}> >// Print the subtree rooted with last child> >if> (leaf ==>false>)> >C[i].traverse();> >}> >// A function to search a key in the subtree rooted with> >// this node.> >BTreeNode search(>int> k)> >{>// returns NULL if k is not present.> >// Find the first key greater than or equal to k> >int> i =>0>;> >while> (i keys[i])> >i++;> >// If the found key is equal to k, return this node> >if> (keys[i] == k)> >return> this>;> >// If the key is not found here and this is a leaf> >// node> >if> (leaf ==>true>)> >return> null>;> >// Go to the appropriate child> >return> C[i].search(k);> >}> }> |
>
>
Python3
# Create a node> class> BTreeNode:> >def> __init__(>self>, leaf>=>False>):> >self>.leaf>=> leaf> >self>.keys>=> []> >self>.child>=> []> # Tree> class> BTree:> >def> __init__(>self>, t):> >self>.root>=> BTreeNode(>True>)> >self>.t>=> t> ># Insert node> >def> insert(>self>, k):> >root>=> self>.root> >if> len>(root.keys)>=>=> (>2> *> self>.t)>-> 1>:> >temp>=> BTreeNode()> >self>.root>=> temp> >temp.child.insert(>0>, root)> >self>.split_child(temp,>0>)> >self>.insert_non_full(temp, k)> >else>:> >self>.insert_non_full(root, k)> ># Insert nonfull> >def> insert_non_full(>self>, x, k):> >i>=> len>(x.keys)>-> 1> >if> x.leaf:> >x.keys.append((>None>,>None>))> >while> i>>=> 0> and> k[>0>] 0]: x.keys[i + 1] = x.keys[i] i -= 1 x.keys[i + 1] = k else: while i>= 0 en k[0] 0]: i -= 1 i += 1 if len(x.child[i].keys) == (2 * self.t) - 1: self.split_child(x, i) if k[0]> x.keys[i][0]: i += 1 self.insert_non_full(x.child[i], k) # Splits het kind def split_child(self, x, i): t = zelf .t y = x.child[i] z = BTreeNode(y.leaf) x.child.insert(i + 1, z) x.keys.insert(i, y.keys[t - 1]) z.keys = y.keys[t: (2 * t) - 1] y.keys = y.keys[0: t - 1] indien niet y.leaf: z.child = y.child[t: 2 * t] y. child = y.child[0: t - 1] # Print de boom def print_tree(self, x, l=0): print('Level ', l, ' ', len(x.keys), end=':') voor i in x.keys: print(i, end=' ') print() l += 1 als len(x.child)> 0: voor i in x.child: self.print_tree(i, l) # Zoeksleutel in de boom def search_key(self, k, x=None): als x niet Geen is: i = 0 terwijl i |
>
>
C#
// C# program to illustrate the sum of two numbers> using> System;> // A BTree> class> Btree {> >public> BTreeNode root;>// Pointer to root node> >public> int> t;>// Minimum degree> >// Constructor (Initializes tree as empty)> >Btree(>int> t)> >{> >this>.root =>null>;> >this>.t = t;> >}> >// function to traverse the tree> >public> void> traverse()> >{> >if> (>this>.root !=>null>)> >this>.root.traverse();> >Console.WriteLine();> >}> >// function to search a key in this tree> >public> BTreeNode search(>int> k)> >{> >if> (>this>.root ==>null>)> >return> null>;> >else> >return> this>.root.search(k);> >}> }> // A BTree node> class> BTreeNode {> >int>[] keys;>// An array of keys> >int> t;>// Minimum degree (defines the range for number> >// of keys)> >BTreeNode[] C;>// An array of child pointers> >int> n;>// Current number of keys> >bool> leaf;>// Is true when node is leaf. Otherwise false> >// Constructor> >BTreeNode(>int> t,>bool> leaf)> >{> >this>.t = t;> >this>.leaf = leaf;> >this>.keys =>new> int>[2 * t - 1];> >this>.C =>new> BTreeNode[2 * t];> >this>.n = 0;> >}> >// A function to traverse all nodes in a subtree rooted> >// with this node> >public> void> traverse()> >{> >// There are n keys and n+1 children, traverse> >// through n keys and first n children> >int> i = 0;> >for> (i = 0; i <>this>.n; i++) {> >// If this is not leaf, then before printing> >// key[i], traverse the subtree rooted with> >// child C[i].> >if> (>this>.leaf ==>false>) {> >C[i].traverse();> >}> >Console.Write(keys[i] +>' '>);> >}> >// Print the subtree rooted with last child> >if> (leaf ==>false>)> >C[i].traverse();> >}> >// A function to search a key in the subtree rooted with> >// this node.> >public> BTreeNode search(>int> k)> >{>// returns NULL if k is not present.> >// Find the first key greater than or equal to k> >int> i = 0;> >while> (i keys[i])> >i++;> >// If the found key is equal to k, return this node> >if> (keys[i] == k)> >return> this>;> >// If the key is not found here and this is a leaf> >// node> >if> (leaf ==>true>)> >return> null>;> >// Go to the appropriate child> >return> C[i].search(k);> >}> }> // This code is contributed by Rajput-Ji> |
>
>
Javascript
// Javascript program to illustrate the sum of two numbers> // A BTree> class Btree> {> >// Constructor (Initializes tree as empty)> >constructor(t)> >{> >this>.root =>null>;> >this>.t = t;> >}> > >// function to traverse the tree> >traverse()> >{> >if> (>this>.root !=>null>)> >this>.root.traverse();> >document.write(>' '>);> >}> > >// function to search a key in this tree> >search(k)> >{> >if> (>this>.root ==>null>)> >return> null>;> >else> >return> this>.root.search(k);> >}> > }> // A BTree node> class BTreeNode> {> >// Constructor> >constructor(t,leaf)> >{> >this>.t = t;> >this>.leaf = leaf;> >this>.keys =>new> Array(2 * t - 1);> >this>.C =>new> Array(2 * t);> >this>.n = 0;> >}> >// A function to traverse all nodes in a subtree rooted with this node> >traverse()> >{> >// There are n keys and n+1 children, traverse through n keys> >// and first n children> >let i = 0;> >for> (i = 0; i <>this>.n; i++) {> > >// If this is not leaf, then before printing key[i],> >// traverse the subtree rooted with child C[i].> >if> (>this>.leaf ==>false>) {> >C[i].traverse();> >}> >document.write(keys[i] +>' '>);> >}> > >// Print the subtree rooted with last child> >if> (leaf ==>false>)> >C[i].traverse();> >}> > >// A function to search a key in the subtree rooted with this node.> >search(k)>// returns NULL if k is not present.> >{> > >// Find the first key greater than or equal to k> >let i = 0;> >while> (i keys[i])> >i++;> > >// If the found key is equal to k, return this node> >if> (keys[i] == k)> >return> this>;> > >// If the key is not found here and this is a leaf node> >if> (leaf ==>true>)> >return> null>;> > >// Go to the appropriate child> >return> C[i].search(k);> >}> }> // This code is contributed by patel2127> |
>
>
Opmerking: De bovenstaande code bevat niet het stuurprogramma. In ons volgende bericht op www.nv.nl bespreken we het volledige programma B-boom inbrengen .
Er zijn twee conventies om een B-Tree te definiëren: de ene is het definiëren op basis van minimale graad, de tweede is het definiëren in volgorde. We hebben de conventie voor het minimumdiploma gevolgd en zullen hetzelfde volgen in de komende berichten op B-Tree. De variabelenamen die in het bovenstaande programma worden gebruikt, blijven ook hetzelfde
aaneenschakeling van tekenreeksen
Toepassingen van B-Trees:
- Het wordt gebruikt in grote databases om toegang te krijgen tot gegevens die op de schijf zijn opgeslagen
- Met de B-Tree kunt u in aanzienlijk minder tijd zoeken naar gegevens in een dataset
- Met de indexeringsfunctie kan indexering op meerdere niveaus worden bereikt.
- De meeste servers gebruiken ook de B-tree-aanpak.
- B-Trees worden in CAD-systemen gebruikt om geometrische gegevens te organiseren en te doorzoeken.
- B-Trees worden ook op andere gebieden gebruikt, zoals natuurlijke taalverwerking, computernetwerken en cryptografie.
Voordelen van B-Trees:
- B-Trees hebben een gegarandeerde tijdscomplexiteit van O(log n) voor basisbewerkingen zoals invoegen, verwijderen en zoeken, waardoor ze geschikt zijn voor grote datasets en realtime toepassingen.
- B-Trees zijn zelfbalancerend.
- Hoge gelijktijdigheid en hoge doorvoer.
- Efficiënt opslaggebruik.
Nadelen van B-Trees:
- B-Trees zijn gebaseerd op schijfgebaseerde datastructuren en kunnen een hoog schijfgebruik hebben.
- Niet in alle gevallen het beste.
- Langzaam in vergelijking met andere datastructuren.
Invoegen en verwijderen:
B-boom inbrengen
B-boom verwijderen