De XOR of exclusieve OF-poort is een speciaal type logische poort dat in digitale elektronica wordt gebruikt om de exclusieve OF-bewerking uit te voeren. De XOR-poort neemt twee ingangen en produceert een uitgang afhankelijk van de combinatie van de twee toegepaste ingangen.

In dit artikel wordt het volledige uitgelegd theorie van de XOR-poort samen met zijn waarheidstabel , Booleaanse expressie , logisch symbool , schakelschema , en meer.

Inhoudsopgave

• Wat is XOR-poort?
• Constructie van XOR-poort met behulp van transistor
• Opgelost voorbeeld van XOR Gate
• Toepassingen van XOR Gate
• Voor-en nadelen

Wat is XOR-poort?

In digitale electronica , is er een logisch circuit genaamd XOR Gate dat twee inputs nodig heeft en een output produceert die het resultaat is van de exclusieve OR-bewerking die wordt uitgevoerd op de combinatie van inputs. Deze logische poort produceert een hoge of logische 1-uitvoer wanneer beide ingangen niet gelijk zijn, anders produceert hij een logische 0-uitvoer.

Operaties van XOR Gate

De werking van de XOR-poort kunnen we als volgt uitleggen:

Retourneert 1, als het aantal logische hoge invoer oneven is.

shellscript uitvoerbaar maken

Retourneert 0, als het aantal logische hoge invoer even is.

Stel dat we twee ingangen hebben, A en B, en de uitgang heet X, dan is de uitdrukking:

De Booleaanse expressie van XOR Gate is als volgt:

string naar int java

X = A’B + AB’

Symbool van XOR-poort

Het logische symbool van de XOR-poort wordt getoond in de volgende afbeelding. In deze figuur vertegenwoordigen de variabelen A en B de invoerregels en A’B + AB’ is de uitvoer van de XOR-poort.

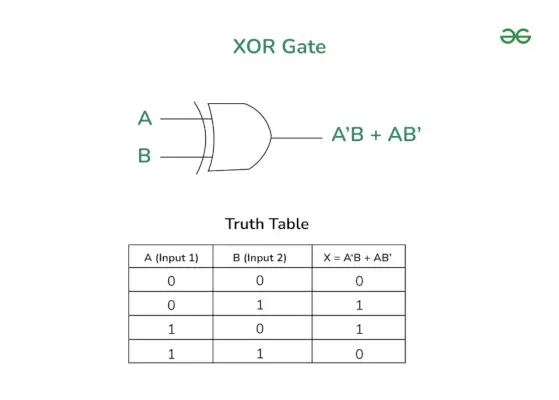
XOR Gate Logic-symbool en waarheidstabel

Waarheidstabel van XOR Gate

De waarheidstabel van een XOR-poort wordt hieronder gegeven. Deze tabel toont de relatie tussen invoer en uitvoer van de XOR-poort. Dit biedt ook informatie over de werking van de XOR-poort voor verschillende invoercombinaties.

Het is belangrijk op te merken dat we geen enkele XOR-poort hebben met drie of meer invoerlijnen. Er zijn slechts twee XOR-poorten met ingangen. Maar als we een XOR-poort nodig hebben die meer dan twee ingangslijnen heeft, combineren we eenvoudigweg meerdere XOR-poorten met twee ingangen om de gewenste XOR-poort te verkrijgen.

Constructie van XOR-poort met behulp van transistor

Wij kunnen exclusief implementeren OF poort met behulp van een transistor. Hier is het circuit dat de verbinding toont van verschillende circuitelementen die worden gecombineerd om de XOR-bewerking te implementeren.

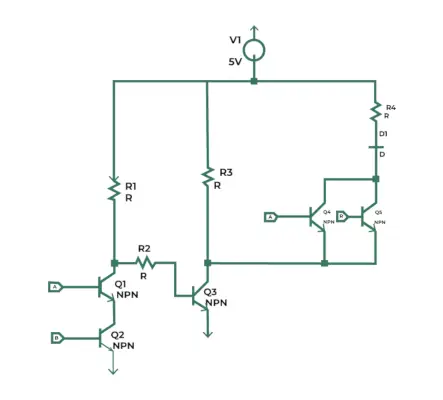
XOR-poort met NPN-transistor

Werking van het circuit

We zullen dit circuit begrijpen met behulp van verschillende invoerscenario's in het geval van een XOR-poort met 2 ingangen:

GEVAL I: Wanneer beide ingangen nul zijn. (A=0, B=0)

Wanneer zowel de ingangen A als B nul zijn dan transistors Q1,Q2,Q4 en Q5 zijn open circuit, dus de LED zal niet gloeien omdat zowel Q4 als Q5 open zijn, dus de negatieve pin van de LED is niet met aarde verbonden.

GEVAL II: Wanneer één ingang logisch hoog is en de andere logisch laag (A=1, B=0)

In dit geval kunnen we gemakkelijk zien dat Q4 nu als een gesloten circuit werkt. Dus de negatieve pin van de LED is via Q4 verbonden met Q3 en uiteindelijk is deze verbonden met aarde, zodat in dit geval de LED gaat branden.

superscript in illustrator

GEVAL III – Wanneer één ingang logisch hoog is en de andere logisch laag (A=0, B=1)

In dit geval kunnen we gemakkelijk zien dat Q5 nu als een gesloten circuit werkt. Dus de negatieve pin van de LED is via Q5 verbonden met Q3 en uiteindelijk is deze verbonden met aarde, zodat in dit geval de LED gaat branden.

GEVAL IV – Wanneer beide ingangen logisch hoog zijn. (A=1, B=1)

In dit geval, wanneer zowel A als B logisch hoog zijn, worden transistor Q1 en Q2 ook geactiveerd, dan zal de stroom rechtstreeks van de +5V-overgang naar aarde gaan via de transistoren Q1 en Q2, en niet in het pad terechtkomen waar Q3 is aangesloten als een resultaattransistor Q3 zal nu fungeren als open circuit en uiteindelijk als negatieve pin LED is losgekoppeld van de aarde, zodat de LED niet gaat branden.

matrices in c-programmering

Toepassingen van XOR Gate

Hier zijn enkele toepassingen van de XOR Gate:

1. Data encryptie: XOR-poorten worden gebruikt in algoritmen voor gegevenscodering. Omdat het wordt gebruikt om gegevens te combineren met een geheime sleutel, wordt het door onbevoegden erg moeilijk te kraken.
2. Vergelijkingscircuits: Het wordt gebruikt in het comparatorcircuit om te controleren of de twee binaire waarden gelijk zijn of niet. Wat betreft hetzelfde type van zowel de ingang geeft het uitgang 0 als voor verschillende ingangen geeft het uitgang 1.
3. Binair optellen en aftrekken: Het helpt bij het bepalen van de som van elk bit en ook bij het combineren met andere logische poorten het afhandelen van leenoperaties.
4. Slippers wisselen: In T-slippers het is gewend aan het circuit dat schakelt bij elke passerende klokpuls.

Enkele andere toepassingen van XOR-poorten zijn adresdecodering, beveiliging en toegangscontrole, het genereren van willekeurige getallen, kloksynchronisatie , frequentiedelercircuits enz.

Voor- en nadelen van XOR Gate

Hier volgt een lijst met de voor- en nadelen van XOR Gate:

Voordelen van XOR Gate

• Het helpt om te detecteren of er een oneven aantal ‘1’ is in de reeks invoer.
• XOR-poorten voeren de exclusieve OF-bewerking uit, wat een fundamentele bewerking is digitale logica .

Nadelen van XOR Gate

• XOR-poort is een complex poortcircuit en als het wordt aangesloten op het circuit dat we gebruiken, veroorzaakt het een verhoogd stroomverbruik en een hogere circuitcomplexiteit.
• Het leidt tot een toename van de voortplantingsvertraging van het circuit.
• Bij het vergroten van het aantal ingangen wordt het circuit steeds complexer, waardoor het moeilijk wordt om fouten te onderhouden en op te sporen.

Opgelost voorbeeld van XOR Gate

Zoek een enkel getal uit een reeks getallen, gegeven het feit dat elk element twee keer voorkomt, behalve dat ene element.

Oplossing: We weten dat XOR van twee dezelfde bits ‘0’ oplevert, dus hier kunnen we zien dat als we de elementen XOR gebruiken, alle elementen die twee keer voorkomen, ‘0’ worden en dat het enige resterende element ons antwoord zou zijn.

Vind ik leuk uit [7,2,2,3,3,4,4,5,5,6,6]

Als we elk van de bovenstaande elementen XOR geven, zullen elementen die een even aantal keren voorkomen '0' opleveren en elementen die een oneven aantal keren voorkomen, de uitvoer opleveren. Uiteindelijk krijgen we 7 als uitvoer, omdat dit element slechts één keer voorkomt en andere elementen een even aantal keren voorkomen.

Conclusie

In dit artikel hebben we geleerd over de XOR-poort. XOR Gate neemt Booleaanse waarden als invoer en retourneert ‘1’ als het aantal logische hoge invoer oneven is en retourneert 0 als het aantal logische hoge invoer even is.

In dit artikel worden de waarheidstabel, de symbolische weergave, het opgeloste voorbeeld en toepassingen uitgelegd die helpen bij een beter begrip van het artikel.

Actrice Rakul Preet Singh

XOR Gate – Veelgestelde vragen

Is XOR-poort een universele logische poort?

Geen enkele XOR-poort is geen universele logische poort, maar kan worden geïmplementeerd door middel van universele logische poorten.

Waarom zijn XOR en XNOR speciale poorten?

XOR- en XNOR-poorten zijn speciaal omdat ze exclusieve operaties uitvoeren essentieel voor foutdetectie, correctie en binaire rekenkunde, waardoor ze fundamenteel zijn in digitale logica en computergebruik.

Wat is XOR voor 2 ingangen?

Voor 2 ingangen, een XOR (exclusief OF) poort voert 1 uit als en slechts als een van de ingangen 1 is en de andere 0. Als beide ingangen hetzelfde zijn, is de uitgang 0.

Wat is het symbool van XOR?

Het symbool voor Exclusief OR(XOR) is ⊕.

Kan XOR 4 ingangen hebben?

Ja, een XOR-poort kan meer dan twee ingangen hebben. In het geval van een XOR-poort met 4 ingangen, de uitvoer is 1 als een oneven aantal ingangen 1 is. Als het aantal 1-en in de ingangen even is, is de uitvoer 0.

Kunnen XOR-poorten worden gebruikt voor optellen en aftrekken?

Ja, XOR-poorten kunnen worden gebruikt om binair optellen en aftrekken uit te voeren in combinatie met andere logische poorten en carry-circuits. Ze zijn essentiële componenten in binaire rekenkundige bewerkingen.

Hoe gedragen XOR-poorten zich in termen van binaire logica en waarheidstabellen?

XOR-poorten vertonen gedrag dat vergelijkbaar is met binaire optelling modulo 2 (bitsgewijze exclusieve OR) en worden gebruikt om binaire gegevens te vergelijken en te manipuleren.