TRAPEZIUMREGEL: DEFINITIE, FORMULE, VOORBEELDEN EN VEELGESTELDE VRAGEN

De trapeziumregel is een van de fundamentele regels van integratie die wordt gebruikt om de basisdefinitie van integratie te definiëren. Het is een veelgebruikte regel en de trapeziumregel wordt zo genoemd omdat hij het gebied onder de curve aangeeft door de curve in kleine trapeziums te verdelen in plaats van in rechthoeken.

Over het algemeen vinden we het gebied onder de curve door het gebied in kleinere rechthoeken te verdelen en vervolgens de som van alle rechthoeken te vinden, maar bij de trapeziumregel wordt het gebied onder de curve verdeeld in trapezoïden, en vervolgens wordt hun som berekend. De trapeziumregel wordt gebruikt om de waarde van de definitieve integralen in numerieke analyse te vinden. Deze regel wordt ook wel de trapeziumregel of de trapeziumregel genoemd. Laten we in dit artikel meer in detail leren over de trapeziumregel, de formule en het bewijs ervan, het voorbeeld en andere.

Wat is de trapeziumregel?

De trapeziumregel is een regel die wordt gebruikt om de waarde van de bepaalde integraal van de vorm te vinden^B∫_Af(x)dx. We weten dat de waarde van de bepaalde integraal^B∫_Af(x) dx is het gebied dat wordt ingesloten onder de curve y = f(x) en de x-as in het interval a en b op de x-as. We berekenen dit gebied door het volledige gebied in verschillende kleine rechthoeken te verdelen en vervolgens de som ervan te berekenen.

Bij de trapeziumregel wordt, zoals de naam doet vermoeden, het gebied onder de curve verdeeld in verschillende trapezoïden en vervolgens wordt hun som gevonden om het oppervlak van de curve te krijgen. De trapeziumregel geeft niet de beste benadering van het gebied onder de curve dan de regel van Simpson, maar toch is het resultaat nauwkeurig genoeg en deze regel is een veelgebruikte regel in de calculus.

Trapeziumvormige regelformule

De trapeziumregelformule is de formule die wordt gebruikt om het gebied onder de curve te vinden. Om nu het gebied onder de curve te vinden met behulp van de trapeziumregel,

Laat y = f(x) een continue curve zijn, gedefinieerd op het gesloten interval [a, b]. Nu verdelen we het gesloten interval [a, b] in n gelijke subintervallen, waarbij elk de breedte heeft van:

Δx = (b – a)/n

Zoals dat,

een = x₀ ₁ ₂<⋯ _N= geb

Met behulp van de trapeziumregelformule kunnen we het gebied onder de curve als volgt vinden:

∫^B_Af(x) dx = Oppervlakte onder de curve = (Δx/2) [y₀+ 2 (en₁+ en₂+ en₃+ ….. + en_n-1) + j_N]

waar, j₀, En₁, En₂,…. En_Nzijn de waarden van de functie bij respectievelijk x = 1, 2, 3, ….., n.

Afleiding van de trapeziumvormige regelformule

De trapeziumregelformule voor het berekenen van het gebied onder de curve wordt afgeleid door het gebied onder de curve in verschillende trapezoïden te verdelen en vervolgens hun som te vinden.

Stelling:

Laat f(x) een continue functie zijn, gedefinieerd op het interval (a, b). Nu verdelen we de intervallen (a, b) in n gelijke subintervallen waarbij de breedte van elk interval is,

Δx = (b – a)/n

zodat a = x₀ ₁ ₂ ₃<….._N= geb

Dan is de trapeziumregelformule:

∫^B_Af(x) dx ≈ △x/2 [f(x₀) + 2f(x₁) + 2f(x₂) +….2f(x_n-1) + f(x_N)]

waar, x_i= a + i△x

Als n → ∞ geeft de RHS van de uitdrukking de definitieve integraal $int_{a}^{b}f(x) dx$

Bewijs:

Deze formule wordt bewezen door het gebied onder de gegeven curve, zoals weergegeven in de bovenstaande figuur, in verschillende trapeziums te verdelen. Het eerste trapezium heeft een hoogte Δx en de lengte van evenwijdige bases is f(x₀) en f(x₁)

De oppervlakte van het eerste trapezium = (1/2) Δx [f(x₀) + f(x₁)]

Op dezelfde manier is de oppervlakte van de resterende trapeziums (1/2)Δx [f(x₁) + f(x₂)], (1/2)Δx [f(x₂) + f(x₃)], enzovoort.

Nu kunnen we zeggen dat,

∫^B_Af(x) dx ≈ (1/2)Δx (f(x₀)+f(x₁) ) + (1/2)Δx (f(x₁)+f(x₂) ) + (1/2)Δx (f(x₂)+f(x₃) ) + … + (1/2)Δx (f(x_n-1) + f(x_N))

Na vereenvoudiging krijgen we:

∫^B_Af(x) dx≈ (Δx/2) (f(x₀)+2 v(x₁)+2 v(x₂)+2 v(x₃)+ … +2f(x_n-1) + f(x_N))

Zo is de trapeziumregel bewezen.

rasterindeling

Hoe trapeziumregel toepassen?

De trapeziumregel bepaalt het gebied onder de curve door het gebied onder de curve in verschillende trapeziums te verdelen en vervolgens de som van alle trapeziums te vinden. De trapeziumregel is niet de perfecte benadering van de waarde van de bepaalde integraal, aangezien deze de kwadratische benadering gebruikt.

We moeten de waarde van de bepaalde integraal, ∫, vinden^B_Af(x)dx. De waarde van de definitieve integraal kan worden berekend met behulp van de trapeziumregel door de onderstaande stappen te volgen:

Stap 1: Markeer de waarde van subintervallen, n en intervallen a en b.

Stap 2: Vind de breedte van het subinterval (△x) met behulp van de formule △x = (b – a)/n

Stap 3: Zet alle waarden in de trapeziumregelformule en vind bij benadering de oppervlakte van de gegeven curve die de definitieve integraal ∫ vertegenwoordigt^B_Af(x)dx

∫ ^B _A f(x) dx ≈ (Δx/2) (f(x ₀ )+2 v(x ₁ )+2 v(x ₂ )+2 v(x ₃ )+ … +2f(x _n-1 ) + f(x _N ))

waar, X _i = a + i△x

Sommatienotatie van trapeziumregel

We weten dat de oppervlakte van een trapezium feitelijk het gemiddelde is van de lengtes van de evenwijdige zijden vermenigvuldigd met de hoogte. Overweeg dus in dit geval een trapezium voor de i^einterval,

$A_{i} = frac{f(x_{i}) + f(x_{i-1})}{2}Delta x$

Omdat de totale oppervlakte de som is van alle oppervlakten,

EEN = EEN₁+ EEN₂+ ….+ A_N

⇒ EEN = $som_{i = 1}^{i = n} A_{i}$

⇒ EEN = $sum_{i = 1}^{i = n}frac{f(x_{i}) + f(x_{i-1})}{2}Delta x$

Dit wordt de sigmanotatie of sommatienotatie van de trapeziumsommen genoemd.

Riemann-sommen

De Riemann vat het werk samen rond het idee om het gebied onder de curve in verschillende rechthoekige delen te verdelen. Naarmate het aantal rechthoeken toeneemt, komt het gebied steeds dichter bij het huidige gebied. In de onderstaande afbeelding is er een functie f(x). Het gebied onder deze functie is verdeeld in vele rechthoeken. Het totale gebied onder de curve is de som van de oppervlakten van alle rechthoeken.

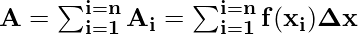
Merk op dat in de bovenstaande afbeelding het rechteruiteinde van de rechthoeken de curve raakt. Dit worden rechts-Riemann-sommen genoemd.

In een ander geval, wanneer het linkeruiteinde van de rechthoeken de curve raakt, zoals weergegeven in de onderstaande afbeelding, worden dit linker Riemann-sommen genoemd.

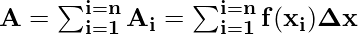
Laten we zeggen dat Δx de breedte is van het interval. Breedte n is het aantal intervallen zoals hierboven vermeld. Vervolgens wordt het gebied van de curve weergegeven door de som gegeven door,

$vet{A = som^{i = n}_{i = 1}A_{i} = som^{i = n}_{i = 1}f(x_{i})Delta x}$

Middelste puntsommen

In de Riemann-sommen raakt het linkeruiteinde of het rechteruiteinde van de rechthoek de curve. In dit geval raakt het middelpunt van de rechthoek de curve. Al het andere is hetzelfde als Riemann-sommen. De onderstaande figuur toont de functie f(x) en verschillende rechthoeken in de middelpuntssommen.

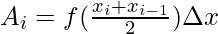
Laten we zeggen A_igeeft het gebied van de i aan^erechthoek. De oppervlakte van deze rechthoek is in dit geval:

constructeur in Java

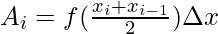
$A_{i} = f(frac{x_i + x_{i-1}}{2}) Delta x$

Nu wordt de totale oppervlakte in de sommatienotatie gegeven door,

$vet{A = som^{i = n}_{i = 1}A_{i} = som^{i = n}_{i = 1}f(frac{x_{i} + x_{ i-1}}{2})Delta x}$

Lees verder,

Integratieformules
Integratie door onderdelen
Differentiatie- en integratieformule

Opgelost voorbeeld van de trapeziumregel

Voorbeeld 1: Zoek de oppervlakte omsloten door de functie f(x) tussen x = 0 tot x = 4 met 4 intervallen.

f(x) = 4

Oplossing:

Hier geldt a = 0, b = 4 en n = 4.

$Delta x= frac{b - a}{n} = Delta x = frac{4 - 0}{4} = Delta x = 1$

$x_{i} = a + iDelta x = x_{i} = 0 + ik = x_{i} = ik$

De trapeziumregel voor n = 4 is:

$T_n = frac{Delta x}{2}(f(x_0) + 2f(x_1) + 2f(x_2) + 2f(x_3) + f(x_4))$

Vervanging van de waarden in deze vergelijking,

$T_n = frac{Delta x}{2}(f(x_0) + 2f(x_1) + 2f(x_2) + 2f(x_3) + f(x_4)) = frac{1}{2}( f(0) + 2f(1) + 2f(2) + 2f(3) + f(4)) = frac{1}{2}(4 + 2(4) + 2(4) + 2(4 ) + 4) = 16$

Voorbeeld 2: Zoek de oppervlakte omsloten door de functie f(x) tussen x = 0 tot x = 3 met 3 intervallen.

f(x) = x

Oplossing:

Hier geldt a = 0, b = 3 en n = 3.

$Delta x= frac{b - a}{n} = Delta x = frac{3 - 0}{3} = Delta x = 1$

$x_{i} = a + iDelta x = x_{i} = 0 + ik = x_{i} = ik$

De trapeziumregel voor n = 3 is:

$T_n = frac{Delta x}{2}(f(x_0) + 2f(x_1) + 2f(x_2) + f(x_3))$

Vervanging van de waarden in deze vergelijking,

$T_n = frac{Delta x}{2}(f(x_0) + 2f(x_1) + 2f(x_2) + f(x_3)) Rechtspijl T_n= frac{1}{2}(f( 0) + 2f(1) + 2f(2) + f(3)) Pijl naar rechts T_n= frac{1}{2}(0 + 2 + 2(2) + 2(3)) Pijl naar rechts T_n= frac{1}{2}(2 + 4 + 6) = 6$

Voorbeeld 3: Zoek de oppervlakte omsloten door de functie f(x) tussen x = 0 tot x = 2 met 2 intervallen.

f(x) = 2x

Oplossing:

Hier geldt a = 0, b = 2 en n = 2.

$Delta x= frac{b - a}{n} = Delta x = frac{2 - 0}{2} = Delta x = 1$

$x_{i} = a + iDelta x = x_{i} = 0 + ik = x_{i} = ik$

De trapeziumregel voor n = 2 is:

$T_n = frac{Delta x}{2}(f(x_0) + 2f(x_1) + f(x_2))$

Vervanging van de waarden in deze vergelijking,

$T_n = frac{Delta x}{2}(f(x_0) + 2f(x_1) + f(x_2)) Rechtspijl T_n= frac{1}{2}(f(0) + 2f( 1) + f(2)) Rechtspijl T_n= frac{1}{2}(0 + 2(2) + 1(4)) Rechtspijl T_n= frac{1}{2}( 8) = 4$

Voorbeeld 4: Zoek de oppervlakte omsloten door de functie f(x) tussen x = 0 tot x = 3 met 3 intervallen.

f(x) = x ²

Oplossing:

Hier geldt a = 0, b = 3 en n = 3.

$Delta x= frac{b - a}{n} = Delta x = frac{3 - 0}{3} = Delta x = 1$

$x_{i} = a + iDelta x = x_{i} = 0 + ik = x_{i} = ik$

De trapeziumregel voor n = 3 is:

$T_n = frac{Delta x}{2}(f(x_0) + 2f(x_1) + 2f(x_2) + f(x_3))$

Vervanging van de waarden in deze vergelijking,
hritik roshan-leeftijd

$T_n = frac{Delta x}{2}(f(x_0) + 2f(x_1) + 2f(x_2) + f(x_3)) Rechtspijl T_n= frac{1}{2}(f( 0) + 2f(1) + 2f(2) + f(3)) Pijl naar rechts T_n= frac{1}{2}(0 + 2(1) + 2(4) + 2(9)) Pijl naar rechts T_n= frac{1}{2}(2 + 8 + 18) = 14$

Voorbeeld 5: Zoek de oppervlakte omsloten door de functie f(x) tussen x = 0 tot x = 4 met 4 intervallen.

f(x) = x ³ + 1

Oplossing:

Hier geldt a = 0, b = 4 en n = 4.

$Delta x= frac{b - a}{n} = Delta x = frac{4 - 0}{4} = Delta x = 1$

$x_{i} = a + iDelta x = x_{i} = 0 + ik = x_{i} = ik$

De trapeziumregel voor n = 4 is:

$T_n = frac{Delta x}{2}(f(x_0) + 2f(x_1) + 2f(x_2) + 2f(x_3) + f(x_4))$

Vervanging van de waarden in deze vergelijking,

$T_n = frac{Delta x}{2}(f(x_0) + 2f(x_1) + 2f(x_2) + 2f(x_3) + f(x_4)) Rechtspijl T_n = frac{1}{ 2}(f(0) + 2f(1) + 2f(2) + 2f(3) + f(4)) Rechtspijl T_n= frac{1}{2}(1 + 2(2) + 2(9) + 2(28) + (65) ) Pijl naar rechts T_n= frac{1}{2}(1 + 4 + 18 + 56 + 65) Pijl naar rechts T_n= 72$

Voorbeeld 6: Zoek de oppervlakte omsloten door de functie f(x) tussen x = 0 tot x = 4 met 4 intervallen.

f(x) = e ^X

Oplossing:

Hier geldt a = 0, b = 4 en n = 4.

$Delta x= frac{b - a}{n} = Delta x = frac{4 - 0}{4} = Delta x = 1$

$x_{i} = a + iDelta x = x_{i} = 0 + ik = x_{i} = ik$

De trapeziumregel voor n = 4 is:

$T_n = frac{Delta x}{2}(f(x_0) + 2f(x_1) + 2f(x_2) + 2f(x_3) + f(x_4))$

Vervanging van de waarden in deze vergelijking,

$T_n = frac{Delta x}{2}(f(x_0) + 2f(x_1) + 2f(x_2) + 2f(x_3) + f(x_4)) Rechtspijl T_n= frac{1}{ 2}(f(0) + 2f(1) + 2f(2) + 2f(3) + f(4)) Rechtspijl T_n= frac{1}{2}(e^0 + 2e + 2e ^2 + 2e^3 + e^4 ) Rightarrow T_n= frac{1}{2} + e + e^2 + e^3 + frac{e^4}{2}$

Toepassingen van de trapeziumregel

Numerieke integratie:

De primaire toepassing van de trapeziumregel is het benaderen van bepaalde integralen. Het wordt gebruikt wanneer de integratie van een functie een uitdaging is en een numerieke benadering haalbaarder is. De trapeziumregel maakt vaak deel uit van meer geavanceerde numerieke integratietechnieken.

Natuurkunde en techniek:

In de natuurkunde en techniek kan de trapeziumregel worden toegepast om grootheden zoals verplaatsing, snelheid en versnelling te berekenen. Wanneer experimentele gegevens bijvoorbeeld met discrete tijdsintervallen worden verzameld, kan de trapeziumregel worden gebruikt om het gebied onder de curve te schatten, waardoor een benadering van de integraal ontstaat.

Economie en Financiën:

De trapeziumregel kan worden toegepast bij financiële modellering om de contante waarde van toekomstige kasstromen te schatten. Dit is vooral handig bij DCF-analyses (Discounted Cash Flow), waarbij het doel is om de netto contante waarde van een investering te berekenen.

Statistieken:

In de statistiek kan de trapeziumregel worden gebruikt om het gebied te schatten onder waarschijnlijkheidsdichtheidsfuncties of cumulatieve verdelingsfuncties. Dit is met name handig in gevallen waarin de exacte vorm van de verdeling onbekend of complex is.

Veelgestelde vragen over de trapeziumregel

Vraag 1: Wat is de trapeziumregel?

Antwoord:

De trapeziumregel is de regel die wordt gebruikt om de definitieve integraal te vinden. Het verdeelt het gebied onder de curve in verschillende trapeziums en vervolgens wordt hun individuele oppervlakte gevonden en vervolgens wordt de som berekend om de waarde van de definitieve integraal te krijgen.

Vraag 2: Wat is de trapeziumregelformule?

Antwoord:

De trapeziumregelformule is:

∫ ^B _A f(x)dx = (Δx/2) (f(x ₀ )+2 v(x ₁ )+2 v(x ₂ )+2 v(x ₃ )+ … +2f(x _n-1 ) + f(x _N ))

Vraag 3: Waarom wordt dit de trapeziumregelformule genoemd?

Antwoord:

De trapeziumregelformule wordt de trapeziumregel genoemd omdat deze het gebied onder de curve in verschillende trapezoïden verdeelt en vervolgens hun oppervlakte wordt berekend door de som van de trapezoïden te vinden.

Vraag 4: Wat is het verschil tussen de trapeziumregel en de Riemann-sommenregel?

Antwoord:

Het belangrijkste verschil tussen de trapeziumregel en de Riemann-somregel is dat de trapeziumregel het gebied onder de curve verdeelt als de trapeziums en vervolgens het gebied vindt door hun som te nemen, terwijl de Riemann-sommen het gebied onder de curve verdelen als het trapezium en vindt vervolgens het gebied door hun som te nemen.