logo

TechCodeview

Sterk verbonden componenten

Sterk verbonden componenten (SCC's) zijn een fundamenteel concept in grafentheorie en algoritmen. In een gerichte graaf is a Sterk verbonden component is een subset van hoekpunten waarbij elk hoekpunt in de subset bereikbaar is vanaf elk ander hoekpunt in dezelfde subset door de gerichte randen te doorlopen. Het vinden van de SCC's van een grafiek kan belangrijke inzichten verschaffen in de structuur en connectiviteit van de grafiek, met toepassingen op verschillende gebieden, zoals analyse van sociale netwerken, webcrawlen en netwerkroutering . Deze tutorial onderzoekt de definitie, eigenschappen en efficiënte algoritmen voor het identificeren van sterk verbonden componenten in grafiekgegevensstructuren

Java vermelden

Inhoudsopgave



Wat zijn Strongly Connected Components (SCC's)?

A sterk verbonden onderdeel van een gerichte graaf is een maximale subgraaf waarin elk paar hoekpunten onderling bereikbaar is. Dit betekent dat er voor elke twee knooppunten A en B in deze subgraaf een pad is van A naar B en een pad van B naar A.

Bijvoorbeeld: De onderstaande grafiek heeft twee sterk verbonden componenten {1,2,3,4} en {5,6,7}, aangezien er een pad is van elk hoekpunt naar elk ander hoekpunt in dezelfde sterk verbonden component.

scc_fianldrawio

Sterk verbonden component



Waarom zijn sterk verbonden componenten (SCC's) belangrijk?

Het begrijpen van SCC's is cruciaal voor verschillende toepassingen, zoals:

  • Netwerk analyse : Identificatie van clusters van nauw met elkaar verbonden knooppunten.
  • Webcrawlers optimaliseren : bepalen van delen van de webgrafiek die nauw met elkaar verbonden zijn.
  • Afhankelijkheidsresolutie : In software: begrijpen welke modules van elkaar afhankelijk zijn.

Verschil tussen verbonden en sterk verbonden componenten ( SCC's)

Connectiviteit in een ongerichte grafiek verwijst naar de vraag of twee hoekpunten van elkaar bereikbaar zijn of niet. Er wordt gezegd dat twee hoekpunten met elkaar zijn verbonden als er een pad tussen zit. In de tussentijd Sterk verbonden is alleen van toepassing op gerichte grafieken . Een subgraaf van een gerichte graaf wordt beschouwd als een Sterk verbonden componenten (SCC) dan en slechts dan als voor elk paar hoekpunten A En B , er bestaat een pad van A naar B en een pad van B naar A . Laten we eens kijken waarom de standaard dfs-methode om aangesloten componenten te vinden in een grafiek kan niet worden gebruikt om sterk verbonden componenten te bepalen.

Beschouw de volgende grafiek:



scc_fianldrawio

Laten we nu beginnen met een dfs bel vanaf hoekpunt 1 om andere hoekpunten te bezoeken.

dfs_finaldrawio

Waarom kan de conventionele DFS-methode niet worden gebruikt om de sterk verbonden componenten te vinden?

Alle hoekpunten kunnen worden bereikt vanaf hoekpunt 1. Maar de hoekpunten 1 en 5,6,7 kunnen zich niet in dezelfde sterk verbonden component bevinden, omdat er geen gericht pad is van hoekpunt 5,6 of 7 naar hoekpunt 1. De grafiek heeft twee sterk verbonden componenten. verbonden componenten {1,2,3,4} en {5,6,7}. De conventionele dfs-methode kan dus niet worden gebruikt om de sterk verbonden componenten te vinden.

verander de naam directory linux

Twee sterk verbonden componenten verbinden via een unidirectionele rand

Twee verschillende verbonden componenten worden één enkele component als er een rand wordt toegevoegd tussen een hoekpunt van de ene component naar een hoekpunt van een andere component. Maar dit is niet het geval bij sterk verbonden componenten. Twee sterk verbonden componenten worden geen enkele sterk verbonden component als er slechts een unidirectionele rand is van de ene SCC naar de andere SCC.

tekenreeks als array

unidrawi-(2)

Brute force-aanpak voor het vinden van sterk verbonden componenten

De eenvoudige methode is om voor elk hoekpunt i (dat geen deel uitmaakt van een sterk component) de hoekpunten te vinden die het deel zullen zijn van een sterk verbonden component die hoekpunt i bevat. Twee hoekpunten i en j zullen zich in dezelfde sterk verbonden component bevinden als er een gericht pad is van hoekpunt i naar hoekpunt j en omgekeerd.

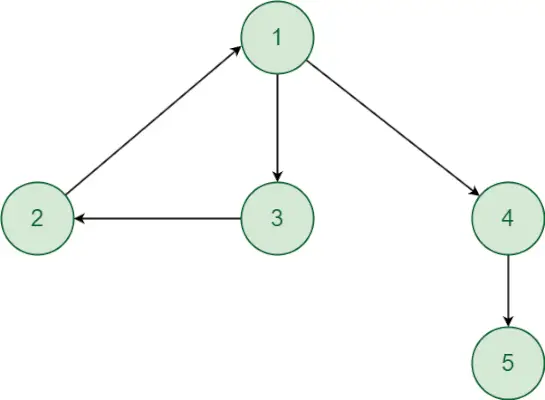
Laten we de aanpak begrijpen met behulp van het volgende voorbeeld:

voorbeeld tekenen

  • Beginnend met hoekpunt 1. Er is een pad van hoekpunt 1 naar hoekpunt 2 en omgekeerd. Op dezelfde manier is er een pad van hoekpunt 1 naar hoekpunt 3 en omgekeerd. Dus hoekpunt 2 en 3 zullen zich in dezelfde sterk verbonden component bevinden als hoekpunt 1. Hoewel er een gericht pad is van hoekpunt 1 naar hoekpunt 4 en hoekpunt 5. Maar er is geen gericht pad van hoekpunt 4,5 naar hoekpunt 1, dus hoekpunt 4 en 5 zullen zich niet in dezelfde Sterk Verbonden Component bevinden als hoekpunt 1. Vertex 1,2 en 3 vormen dus een Sterk Verbonden Component.
  • Voor Vertex 2 en 3 is de Sterk Verbonden Component al bepaald.
  • Voor hoekpunt 4 is er een pad van hoekpunt 4 naar hoekpunt 5, maar er is geen pad van hoekpunt 5 naar hoekpunt 4. Hoekpunt 4 en 5 bevinden zich dus niet in dezelfde sterk verbonden component. Zowel Vertex 4 als Vertex 5 zullen dus deel uitmaken van Single Strongly Connected Component.
  • Er zullen dus 3 sterk verbonden componenten zijn: {1,2,3}, {4} en {5}.

Hieronder vindt u de implementatie van bovenstaande aanpak:

C++ 
#include  using namespace std; class GFG { public:  // dfs Function to reach destination  bool dfs(int curr, int des, vector>& bijvoeglijk naamwoord, vector & vis) {// If curr node is de bestemming return true if (curr == des) { return true;  } vis[curr] = 1;  for (auto x: adj[curr]) { if (!vis[x]) { if (dfs(x, des, adj, vis)) { return true;  } } } return false;  } // Om te bepalen of er een pad is van bron naar // bestemming bool isPath(int src, int des, vector>& bijvoeglijk naamwoord) { vector vis(adj.grootte() + 1, 0);  return dfs(src, des, adj, vis);  } // Functie om alle sterk verbonden // componenten van een grafiek terug te geven.  vector> vindSCC(int n, vector>& a) {// Slaat alle sterk verbonden componenten op.  vector> ans;  // Slaat op of een hoekpunt deel uitmaakt van een Strongly // Connected Component-vector is_scc(n + 1, 0);  vector> bijvoeglijk naamwoord(n + 1);  voor (int i = 0; ik< a.size(); i++) {  adj[a[i][0]].push_back(a[i][1]);  }  // Traversing all the vertices  for (int i = 1; i <= n; i++) {  if (!is_scc[i]) {  // If a vertex i is not a part of any SCC  // insert it into a new SCC list and check  // for other vertices whether they can be  // thr part of thidl ist.  vector scc;  scc.push_back(i);  voor (int j = ik + 1; j<= n; j++) {  // If there is a path from vertex i to  // vertex j and vice versa put vertex j  // into the current SCC list.  if (!is_scc[j] && isPath(i, j, adj)  && isPath(j, i, adj)) {  is_scc[j] = 1;  scc.push_back(j);  }  }  // Insert the SCC containing vertex i into  // the final list.  ans.push_back(scc);  }  }  return ans;  } }; // Driver Code Starts int main() {  GFG obj;  int V = 5;  vector> randen{ { 1, 3 }, { 1, 4 }, { 2, 1 }, { 3, 2 }, { 4, 5 } };  vector> ans = obj.findSCC(V, randen);  uit<< 'Strongly Connected Components are:
';  for (auto x : ans) {  for (auto y : x) {  cout << y << ' ';  }  cout << '
';  } }>
Java 
import java.util.ArrayList; import java.util.List; class GFG {  // dfs Function to reach destination  boolean dfs(int curr, int des, List> bijvoeglijk naamwoord, Lijst vis) {// If curr node is de bestemming return true if (curr == des) { return true;  } vis.set(curr, 1);  for (int x: adj.get(curr)) { if (vis.get(x) == 0) { if (dfs(x, des, adj, vis)) { return true;  } } } return false;  } // Om aan te geven of er een pad is van bron naar // bestemming boolean isPath(int src, int des, List> bijvoeglijk naamwoord) { Lijst vis = nieuwe ArrayList(adj.size() + 1);  voor (int i = 0; ik<= adj.size(); i++) {  vis.add(0);  }  return dfs(src, des, adj, vis);  }  // Function to return all the strongly connected  // component of a graph.  List> findSCC(int n, Lijst> a) {// Slaat alle sterk verbonden componenten op.  Lijst> ans = nieuwe ArrayList();  // Slaat op of een hoekpunt deel uitmaakt van een Strongly // Connected Component List is_scc = nieuwe ArrayList(n + 1);  voor (int i = 0; ik<= n; i++) {  is_scc.add(0);  }  List> bijvoeglijk naamwoord = nieuwe ArrayList();  voor (int i = 0; ik<= n; i++) {  adj.add(new ArrayList());  }  for (List edge : a) { bijvoeglijk naamwoord.get(edge.get(0)).add(edge.get(1));  } // Alle hoekpunten doorlopen voor (int i = 1; i<= n; i++) {  if (is_scc.get(i) == 0) {  // If a vertex i is not a part of any SCC  // insert it into a new SCC list and check  // for other vertices whether they can be  // the part of this list.  List scc = nieuwe ArrayList();  scc.add(i);  voor (int j = ik + 1; j<= n; j++) {  // If there is a path from vertex i to  // vertex j and vice versa, put vertex j  // into the current SCC list.  if (is_scc.get(j) == 0 && isPath(i, j, adj)  && isPath(j, i, adj)) {  is_scc.set(j, 1);  scc.add(j);  }  }  // Insert the SCC containing vertex i into  // the final list.  ans.add(scc);  }  }  return ans;  } } public class Main {  public static void main(String[] args) {  GFG obj = new GFG();  int V = 5;  List> randen = nieuwe ArrayList();  randen.add(nieuwe ArrayList(Lijst.van(1, 3)));  randen.add(nieuwe ArrayList(Lijst.van(1, 4)));  randen.add(nieuwe ArrayList(Lijst.van(2, 1)));  randen.add(nieuwe ArrayList(Lijst.van(3, 2)));  randen.add(nieuwe ArrayList(Lijst.van(4, 5)));  Lijst> ans = obj.findSCC(V, randen);  System.out.println('Sterk verbonden componenten zijn:');  voor (Lijst x: ans) { for (int y: x) { Systeem.out.print(y + ' ');  } Systeem.out.println();  } } } // Deze code is bijgedragen door shivamgupta310570>
Python 
class GFG: # dfs Function to reach destination def dfs(self, curr, des, adj, vis): # If current node is the destination, return True if curr == des: return True vis[curr] = 1 for x in adj[curr]: if not vis[x]: if self.dfs(x, des, adj, vis): return True return False # To tell whether there is a path from source to destination def isPath(self, src, des, adj): vis = [0] * (len(adj) + 1) return self.dfs(src, des, adj, vis) # Function to return all the strongly connected components of a graph. def findSCC(self, n, a): # Stores all the strongly connected components. ans = [] # Stores whether a vertex is a part of any Strongly Connected Component is_scc = [0] * (n + 1) adj = [[] for _ in range(n + 1)] for i in range(len(a)): adj[a[i][0]].append(a[i][1]) # Traversing all the vertices for i in range(1, n + 1): if not is_scc[i]: # If a vertex i is not a part of any SCC, insert it into a new SCC list # and check for other vertices whether they can be part of this list. scc = [i] for j in range(i + 1, n + 1): # If there is a path from vertex i to vertex j and vice versa, # put vertex j into the current SCC list. if not is_scc[j] and self.isPath(i, j, adj) and self.isPath(j, i, adj): is_scc[j] = 1 scc.append(j) # Insert the SCC containing vertex i into the final list. ans.append(scc) return ans # Driver Code Starts if __name__ == '__main__': obj = GFG() V = 5 edges = [ [1, 3], [1, 4], [2, 1], [3, 2], [4, 5] ] ans = obj.findSCC(V, edges) print('Strongly Connected Components are:') for x in ans: for y in x: print(y, end=' ') print() # This code is contributed by shivamgupta310570>
C# 
using System; using System.Collections.Generic; class GFG {  // dfs Function to reach destination  public bool Dfs(int curr, int des, List> bijvoeglijk naamwoord, Lijst vis) {// Als curr node de bestemming is, return true if (curr == des) { return true;  } vis[curr] = 1;  foreach (var x in adj[curr]) { if (vis[x] == 0) { if (Dfs(x, des, adj, vis)) { return true;  } } } return false;  } // Om aan te geven of er een pad is van bron naar bestemming public bool IsPath(int src, int des, List> bijvoeglijk naamwoord) { var show = nieuwe lijst (adj. Aantal + 1);  voor (int i = 0; ik< adj.Count + 1; i++)  {  vis.Add(0);  }  return Dfs(src, des, adj, vis);  }  // Function to return all the strongly connected components of a graph  public List> VindSCC(int n, Lijst> a) {// Slaat alle sterk verbonden componenten op var ans = new List>();  // Slaat op of een hoekpunt deel uitmaakt van een sterk verbonden component var isScc = new List (n + 1);  voor (int i = 0; ik< n + 1; i++)  {  isScc.Add(0);  }  var adj = new List>(n+1);  voor (int i = 0; ik< n + 1; i++)  {  adj.Add(new List ());  } voor (int i = 0; i< a.Count; i++)  {  adj[a[i][0]].Add(a[i][1]);  }  // Traversing all the vertices  for (int i = 1; i <= n; i++)  {  if (isScc[i] == 0)  {  // If a vertex i is not a part of any SCC  // insert it into a new SCC list and check  // for other vertices whether they can be  // the part of this list.  var scc = new List ();  scc.Toevoegen(i);  voor (int j = ik + 1; j<= n; j++)  {  // If there is a path from vertex i to  // vertex j and vice versa, put vertex j  // into the current SCC list.  if (isScc[j] == 0 && IsPath(i, j, adj) && IsPath(j, i, adj))  {  isScc[j] = 1;  scc.Add(j);  }  }  // Insert the SCC containing vertex i into  // the final list.  ans.Add(scc);  }  }  return ans;  } } // Driver Code Starts class Program {  static void Main(string[] args)  {  GFG obj = new GFG();  int V = 5;  List> randen = nieuwe lijst> { nieuwe lijst { 1, 3 }, nieuwe lijst { 1, 4 }, nieuwe lijst { 2, 1 }, nieuwe lijst { 3, 2 }, nieuwe lijst { 4, 5 } };  Lijst> ans = obj.FindSCC(V, randen);  Console.WriteLine('Sterk verbonden componenten zijn:');  foreach (var x in ans) { foreach (var y in x) { Console.Write(y + ' ');  } Console.WriteLine();  } } } // Deze code is bijgedragen door shivamgupta310570>
Javascript 
class GFG {  // Function to reach the destination using DFS  dfs(curr, des, adj, vis) {  // If the current node is the destination, return true  if (curr === des) {  return true;  }  vis[curr] = 1;  for (let x of adj[curr]) {  if (!vis[x]) {  if (this.dfs(x, des, adj, vis)) {  return true;  }  }  }  return false;  }  // Check whether there is a path from source to destination  isPath(src, des, adj) {  const vis = new Array(adj.length + 1).fill(0);  return this.dfs(src, des, adj, vis);  }  // Function to find all strongly connected components of a graph  findSCC(n, a) {  // Stores all strongly connected components  const ans = [];  // Stores whether a vertex is part of any Strongly Connected Component  const is_scc = new Array(n + 1).fill(0);  const adj = new Array(n + 1).fill().map(() =>[]);  voor (laat i = 0; i< a.length; i++) {  adj[a[i][0]].push(a[i][1]);  }  // Traversing all the vertices  for (let i = 1; i <= n; i++) {  if (!is_scc[i]) {  // If a vertex i is not part of any SCC,  // insert it into a new SCC list and check  // for other vertices that can be part of this list.  const scc = [i];  for (let j = i + 1; j <= n; j++) {  // If there is a path from vertex i to  // vertex j and vice versa, put vertex j  // into the current SCC list.  if (!is_scc[j] && this.isPath(i, j, adj) && this.isPath(j, i, adj)) {  is_scc[j] = 1;  scc.push(j);  }  }  // Insert the SCC containing vertex i into the final list.  ans.push(scc);  }  }  return ans;  } } // Driver Code Starts const obj = new GFG(); const V = 5; const edges = [  [1, 3], [1, 4], [2, 1], [3, 2], [4, 5] ]; const ans = obj.findSCC(V, edges); console.log('Strongly Connected Components are:'); for (let x of ans) {  console.log(x.join(' ')); } // This code is contributed by shivamgupta310570>
Uitvoer 
Strongly Connected Components are: 1 2 3 4 5>

Tijdcomplexiteit: O(n * (n + m)), omdat we voor elk paar hoekpunten controleren of er een pad tussen bestaat.
Hulpruimte: O (N)

string naar geheel getal converteren

Efficiënte aanpak voor het vinden van sterk verbonden componenten (SCC's)

Om SCC's in een grafiek te vinden, kunnen we algoritmen gebruiken zoals Het algoritme van Kosaraju of Het algoritme van Tarjan . Laten we deze algoritmen stap voor stap verkennen.

1. Het algoritme van Kosaraju :

Het algoritme van Kosaraju omvat twee hoofdfasen:

  1. Diepte-eerst zoeken (DFS) uitvoeren op de originele grafiek :
    • We voeren eerst een DFS uit op de originele grafiek en registreren de eindtijden van knooppunten (dat wil zeggen het tijdstip waarop de DFS klaar is met het volledig verkennen van een knooppunt).
  2. DFS uitvoeren op de getransponeerde grafiek :
    • Vervolgens keren we de richting van alle randen in de grafiek om om de getransponeerde grafiek te creëren.
    • Vervolgens voeren we een DFS uit op de getransponeerde grafiek, waarbij we knooppunten beschouwen in afnemende volgorde van hun eindtijden geregistreerd in de eerste fase.
    • Elke DFS-traversal in deze fase levert ons één SCC op.

Hier is een vereenvoudigde versie van het algoritme van Kosaraju:

  1. DFS op originele grafiek : Eindtijden vastleggen.
  2. Transponeer de grafiek : Draai alle randen om.
  3. DFS op getransponeerde grafiek : Verwerk knooppunten in volgorde van afnemende eindtijden om SCC's te vinden.

2. Het algoritme van Tarjan :

Het algoritme van Tarjan is efficiënter omdat het SCC's in één enkele DFS-pas vindt met behulp van een stapel en wat extra boekhouding:

  1. DFS-doorgang : houd tijdens de DFS een index bij voor elk knooppunt en de kleinste index (low-link-waarde) die vanaf het knooppunt kan worden bereikt.
  2. Stapel : houd de knooppunten bij die zich momenteel in de recursiestapel bevinden (een deel van de huidige SCC wordt onderzocht).
  3. SCC's identificeren : Wanneer de low-link-waarde van een knooppunt gelijk is aan de index, betekent dit dat we een SCC hebben gevonden. Haal alle knooppunten uit de stapel totdat we het huidige knooppunt bereiken.

Hier is een vereenvoudigd overzicht van het algoritme van Tarjan:

  1. Initialiserenindex>naar 0.
  2. Voer voor elk niet-bezocht knooppunt DFS uit.
    • Stel de index en de low-link-waarde van het knooppunt in.
    • Duw het knooppunt op de stapel.
    • Voor elk aangrenzend knooppunt voert u DFS uit als deze niet wordt bezocht, of werkt u de low-link-waarde bij als deze zich in de stapel bevindt.
    • Als de low-link-waarde van het knooppunt gelijk is aan de index, knalt u knooppunten uit de stapel om een ​​SCC te vormen.

Conclusie

Begrijpen en vinden sterk verbonden componenten in een gerichte grafiek is essentieel voor veel toepassingen in de informatica. van Kosaraju En Die van Tarjan algoritmen zijn efficiënte manieren om SCC's te identificeren, elk met hun eigen aanpak en voordelen. Door deze concepten onder de knie te krijgen, kun je de structuur en het gedrag van complexe netwerken beter analyseren en optimaliseren.