Een NFA kan nul, één of meer dan één zet vanuit een bepaalde status op een bepaald invoersymbool hebben. Een NFA kan ook NULL-zetten hebben (zetten zonder invoersymbool). Aan de andere kant heeft DFA één en slechts één beweging vanuit een bepaalde staat op een bepaald invoersymbool.

Stappen voor het converteren van NFA naar DFA:

Stap 1: Converteer de gegeven NFA naar de equivalente transitietabel
Om de NFA naar de equivalente transitietabel te converteren, moeten we alle toestanden, invoersymbolen en de transitieregels vermelden. De overgangsregels worden weergegeven in de vorm van een matrix, waarbij de rijen de huidige status vertegenwoordigen, de kolommen het invoersymbool vertegenwoordigen en de cellen de volgende status vertegenwoordigen.

Stap 2: Maak de startstatus van de DFA
De startstatus van de DFA is de verzameling van alle mogelijke startstatussen in de NFA. Deze set wordt de epsilon-afsluiting van de startstatus van de NFA genoemd. De epsilon-afsluiting is de verzameling van alle toestanden die vanaf de starttoestand kunnen worden bereikt door het volgen van epsilon (?)-overgangen.

np waar

Stap 3: Maak de overgangstabel van de DFA
De overgangstabel van de DFA is vergelijkbaar met de overgangstabel van de NFA, maar in plaats van individuele staten vertegenwoordigen de rijen en kolommen reeksen staten. Voor elk invoersymbool bevat de corresponderende cel in de transitietabel de epsilon-afsluiting van de reeks toestanden die zijn verkregen door het volgen van de transitieregels in de transitietabel van de NFA.

Stap 4: Maak de eindstatussen van de DFA
De eindtoestanden van de DFA zijn de reeksen staten die ten minste één eindtoestand uit de NFA bevatten.

Stap 5: Vereenvoudig de DFA
De in de voorgaande stappen verkregen DFA kan onnodige toestanden en overgangen bevatten. Om de DFA te vereenvoudigen, kunnen we de volgende technieken gebruiken:

10 1 miljoen

• Onbereikbare staten verwijderen: staten die niet vanuit de startstatus kunnen worden bereikt, kunnen uit de DFA worden verwijderd.
• Verwijder dode staten: staten die niet tot een definitieve status kunnen leiden, kunnen uit de DFA worden verwijderd.
• Equivalente staten samenvoegen: staten die dezelfde overgangsregels hebben voor alle invoersymbolen kunnen worden samengevoegd tot één enkele staat.

Stap 6: Herhaal stap 3-5 totdat geen verdere vereenvoudiging meer mogelijk is
Na het vereenvoudigen van de DFA herhalen we stap 3-5 totdat verdere vereenvoudiging niet meer mogelijk is. De uiteindelijk verkregen DFA is het geminimaliseerde DFA-equivalent aan de gegeven NFA.

Voorbeeld: Beschouw de volgende NFA, weergegeven in figuur 1.

Hieronder volgen de verschillende parameters voor NFA. Q = { q0, q1, q2 } ? = ( een, b ) F = { q2 } ? (Overgangsfunctie van NFA)

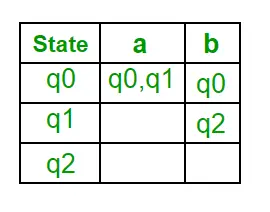
Stap 1: Q’ = ? Stap 2: Q’ = {q0} Stap 3: Zoek voor elke toestand in Q’ de toestanden voor elk invoersymbool. Momenteel is de status in Q’ q0. Vind zetten vanaf q0 op invoersymbool a en b met behulp van de transitiefunctie van NFA en update de transitietabel van DFA. ?’ (Overgangsfunctie van DFA)

Nu wordt { q0, q1 } als één enkele toestand beschouwd. Aangezien de invoer ervan niet in Q’ staat, voegt u deze toe aan Q’. Dus Q' = { q0, { q0, q1 } } Nu zijn bewegingen van toestand { q0, q1 } op verschillende invoersymbolen niet aanwezig in de overgangstabel van DFA, we zullen het als volgt berekenen: ?' , een ) = ? (q0, a) ? ? ( q1, a ) = { q0, q1 } ?’ ( { q0, q1 }, b ) = ? (q0, b) ? ? ( q1, b ) = { q0, q2 } Nu gaan we de transitietabel van DFA bijwerken. ?’ (Overgangsfunctie van DFA)

arp-a-opdracht

Nu wordt { q0, q2 } als één enkele toestand beschouwd. Aangezien de invoer ervan niet in Q’ staat, voegt u deze toe aan Q’. Dus Q' = { q0, { q0, q1 }, { q0, q2 } } Nu zijn bewegingen van toestand {q0, q2} op verschillende invoersymbolen niet aanwezig in de overgangstabel van DFA, we zullen het als volgt berekenen: ?' ({ q0, q2 }, een ) = ? (q0, a) ? ? ( q2, a ) = { q0, q1 } ?’ ( { q0, q2 }, b ) = ? (q0, b) ? ? ( q2, b ) = { q0 } Nu gaan we de transitietabel van DFA bijwerken. ?’ (Overgangsfunctie van DFA)

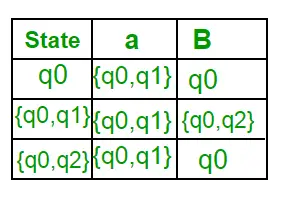
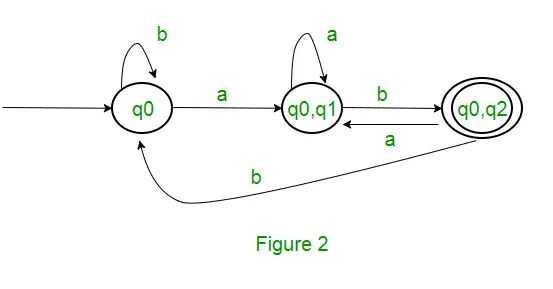
Omdat er geen nieuwe status wordt gegenereerd, zijn we klaar met de conversie. De eindstatus van DFA zal de status zijn die q2 als component heeft, d.w.z. {q0, q2} Hieronder volgen de verschillende parameters voor DFA. Q’ = { q0, { q0, q1 }, { q0, q2 } } ? = ( a, b ) F = { { q0, q2 } } en overgangsfunctie ?’ zoals hierboven weergegeven. De uiteindelijke DFA voor bovenstaande NFA is weergegeven in Figuur 2.

Opmerking : Soms is het niet eenvoudig om reguliere expressies naar DFA te converteren. Eerst kunt u reguliere expressies naar NFA converteren en vervolgens NFA naar DFA.

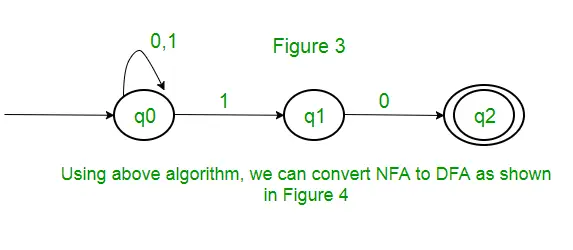
Vraag : Het aantal toestanden in de minimaal deterministische eindige automaat dat overeenkomt met de reguliere expressie (0 + 1)* (10) is ____________.

Oplossing : Eerst zullen we een NFA maken voor de bovenstaande uitdrukking. Om een ​​NFA te maken voor (0 + 1)*, zal NFA zich in dezelfde status q0 bevinden op invoersymbool 0 of 1. Vervolgens voegen we voor aaneenschakeling twee zetten toe (q0 tot q1 voor 1 en q1 tot q2 voor 0) zoals weergegeven in Figuur 3.

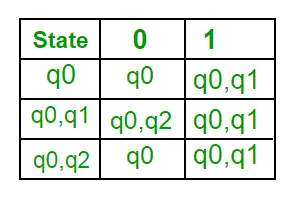
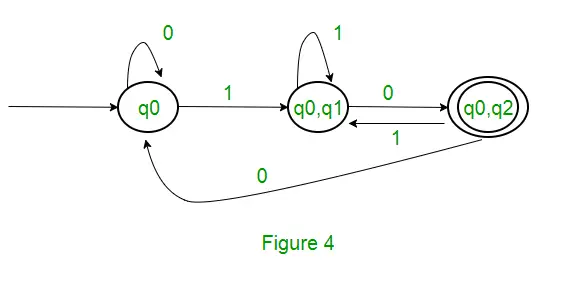
Dit artikel is bijgedragen door Sonal Tuteja.