Binaire zoekboom is een datastructuur die in de computerwetenschappen wordt gebruikt voor het ordenen en opslaan van gegevens op een gesorteerde manier. De binaire zoekboom volgt alle eigenschappen van de binaire boom en zijn links child bevat waarden die kleiner zijn dan het bovenliggende knooppunt en de rechts child bevat waarden die groter zijn dan het bovenliggende knooppunt. Deze hiërarchische structuur maakt efficiënt werken mogelijk Zoeken , Plaatsing , En Verwijdering bewerkingen op de gegevens die in de boom zijn opgeslagen.
Binaire zoekboom
Inhoudsopgave
- Wat is binaire zoekboom?
- Eigenschappen van binaire zoekboom
- Omgaan met dubbele waarden in de binaire zoekboom
- Operaties uitgevoerd op een BST
- 1. Een knooppunt zoeken in BST
- 2. Voeg een knooppunt in een BST in
- 3. Verwijder een knooppunt van BST
- 4. Traversal (in volgorde van BST)
- Toepassingen van BST
- Voordelen
- Nadelen
- FAQ’s (veelgestelde vragen) over de binaire zoekboom:
Wat is binaire zoekboom?
Binaire zoekboom (BST) is een speciaal soort binaire boom waarbij het linkerkind van een knooppunt een waarde heeft die kleiner is dan de waarde van het knooppunt en het rechterkind een waarde heeft die groter is dan de waarde van het knooppunt. Deze eigenschap wordt de BST-eigenschap genoemd en maakt het mogelijk om efficiënt elementen in de boom te zoeken, in te voegen en te verwijderen.
Eigenschappen van binaire zoekboom:
- De linker subboom van een knooppunt bevat alleen knooppunten met sleutels die kleiner zijn dan de sleutel van het knooppunt.
- De rechter subboom van een knooppunt bevat alleen knooppunten met sleutels die groter zijn dan de sleutel van het knooppunt.
- Dit betekent dat alles links van de wortel kleiner is dan de waarde van de wortel en dat alles rechts van de wortel groter is dan de waarde van de wortel. Dankzij deze prestaties is binair zoeken heel eenvoudig.
- De linker en rechter subboom moeten elk ook een binaire zoekboom zijn.
- Er mogen geen dubbele knooppunten zijn (BST kan dubbele waarden hebben met verschillende verwerkingsbenaderingen)
Omgaan met dubbele waarden in de binaire zoekboom:
- We moeten een consistent proces volgen, d.w.z. de dubbele waarde links opslaan of de dubbele waarde rechts van de root opslaan, maar wees consistent met uw aanpak.
Basisbewerkingen in de binaire zoekboom:
1. Een knooppunt zoeken in BST:
Zoeken in BST betekent het lokaliseren van een specifiek knooppunt in de datastructuur. In de binaire zoekboom is het zoeken naar een knooppunt eenvoudig vanwege de specifieke volgorde. De stappen voor het zoeken naar een knooppunt in de binaire zoekboom worden als volgt weergegeven:
- Vergelijk eerst het te doorzoeken element met het hoofdelement van de boom.
- Als root overeenkomt met het doelelement, retourneer dan de locatie van het knooppunt.
- Als het niet overeenkomt, controleer dan of het item kleiner is dan het hoofdelement. Als het kleiner is dan het hoofdelement, ga dan naar de linker subboom.
- Als het groter is dan het hoofdelement, ga dan naar de rechter subboom.
- Herhaal de bovenstaande procedure recursief totdat de match is gevonden.
- Als het element niet wordt gevonden of niet aanwezig is in de boom, retourneert u NULL.
Laten we nu het zoeken in de binaire boom begrijpen aan de hand van een voorbeeld:
niet-deterministische eindige automaten
Hieronder wordt een BST gegeven en moeten we zoeken naar element 6.
Code:
Hieronder ziet u de implementatie van zoeken in BST:
C++ // C++ function to search a given key in a given BST #include using namespace std; struct node { int key; struct node *left, *right; }; // A utility function to create a new BST node struct node* newNode(int item) { struct node* temp = new struct node; temp->sleutel = artikel; temp->links = temp->rechts = NULL; retourtemperatuur; } // Een hulpprogrammafunctie om in te voegen // een nieuw knooppunt met een bepaalde sleutel in BST struct node* insert(struct node* node, int key) {// Als de boom leeg is, retourneert u een nieuw knooppunt if (node == NULL ) return newNode(sleutel); // Anders ga je terug in de boom als (key< node->sleutel) knooppunt->links = invoegen(knooppunt->links, sleutel); else if (sleutel> knooppunt->sleutel) knooppunt->rechts = insert(knooppunt->rechts, sleutel); // Retourneer het (ongewijzigde) knooppunt-pointer-retourknooppunt; } // Hulpprogrammafunctie om een sleutel te zoeken in een BST struct node* search(struct node* root, int key) root->key == key) return root; // Sleutel is groter dan de sleutel van root if (root->key< key) return search(root->rechts, sleutel); // Sleutel is kleiner dan de sleutelretourzoekopdracht van root (root->left, key);> C // C function to search a given key in a given BST #include #include struct node { int key; struct node *left, *right; }; // A utility function to create a new BST node struct node* newNode(int item) { struct node* temp = (struct node*)malloc(sizeof(struct node)); temp->sleutel = artikel; temp->links = temp->rechts = NULL; retourtemperatuur; } // Een hulpprogrammafunctie om in te voegen // een nieuw knooppunt met een bepaalde sleutel in BST struct node* insert(struct node* node, int key) {// Als de boom leeg is, retourneert u een nieuw knooppunt if (node == NULL ) return newNode(sleutel); // Anders ga je terug in de boom als (key< node->sleutel) knooppunt->links = invoegen(knooppunt->links, sleutel); else if (sleutel> knooppunt->sleutel) knooppunt->rechts = insert(knooppunt->rechts, sleutel); // Retourneer het (ongewijzigde) knooppunt-pointer-retourknooppunt; } // Hulpprogrammafunctie om een sleutel te zoeken in een BST struct node* search(struct node* root, int key)> Java // Java program to search a given key in a given BST class Node { int key; Node left, right; public Node(int item) { key = item; left = right = null; } } class BinarySearchTree { Node root; // Constructor BinarySearchTree() { root = null; } // A utility function to insert // a new node with given key in BST Node insert(Node node, int key) { // If the tree is empty, return a new node if (node == null) { node = new Node(key); return node; } // Otherwise, recur down the tree if (key < node.key) node.left = insert(node.left, key); else if (key>knooppunt.sleutel) knooppunt.rechts = invoegen(knooppunt.rechts, sleutel); // Retourneer het (ongewijzigde) knooppunt-pointer-retourknooppunt; } // Hulpprogrammafunctie om een sleutel te zoeken in een BST-knooppuntzoekopdracht (knooppuntroot, int-sleutel) // Basisgevallen: root is null of sleutel is aanwezig in root if (root == null> Python # Python3 function to search a given key in a given BST class Node: # Constructor to create a new node def __init__(self, key): self.key = key self.left = None self.right = None # A utility function to insert # a new node with the given key in BST def insert(node, key): # If the tree is empty, return a new node if node is None: return Node(key) # Otherwise, recur down the tree if key < node.key: node.left = insert(node.left, key) elif key>node.key: node.right = insert(node.right, key) # Retourneert de (ongewijzigde) knooppuntaanwijzer return node # Hulpprogrammafunctie om een sleutel te zoeken in een BST def-zoekopdracht (root, sleutel): # Basisgevallen: root is null of sleutel is aanwezig in de root als root Geen is of root.key == sleutel: return root # Sleutel is groter dan de sleutel van root als root.key< key: return search(root.right, key) # Key is smaller than root's key return search(root.left, key)>
JavaScript // Javascript function to search a given key in a given BST class Node { constructor(key) { this.key = key; this.left = null; this.right = null; } } // A utility function to insert // a new node with given key in BST function insert(node, key) { // If the tree is empty, return a new node if (node === null) { return new Node(key); } // Otherwise, recur down the tree if (key < node.key) { node.left = insert(node.left, key); } else if (key>knooppunt.sleutel) { knooppunt.rechts = invoegen(knooppunt.rechts, sleutel); } // Retourneer het (ongewijzigde) knooppunt-pointer-retourknooppunt; } // Hulpprogramma-functie om een sleutel te zoeken in een BST-functie search(root, key) {// Basisgevallen: root is null of sleutel is aanwezig in root if (root === null || root.key === sleutel ) { retourwortel; } // Sleutel is groter dan de sleutel van root if (root.key< key) { return search(root.right, key); } // Key is smaller than root's key return search(root.left, key); }>
2. Voeg een knooppunt in een BST in :
Er wordt altijd een nieuwe sleutel in de vleugel gestoken. Begin met het zoeken naar een sleutel vanaf de wortel tot een bladknooppunt. Zodra een bladknooppunt is gevonden, wordt het nieuwe knooppunt toegevoegd als een onderliggend knooppunt van het bladknooppunt.
Code:
Hieronder ziet u de implementatie van het invoegen van een enkel knooppunt in de binaire zoekboom:
C++ // Given Node Structure struct node { int key; struct node *left, *right; }; // Function to create a new BST node struct node* newNode(int item) { struct node* temp = (struct node*)malloc( sizeof(struct node)); temp->sleutel = artikel; temp->links = temp->rechts = NULL; retourtemperatuur; } // Functie om een nieuw knooppunt in te voegen met // gegeven sleutel in BST struct node* insert(struct node* node, int key) {// Als de boom leeg is, retourneer dan een nieuw knooppunt if (node == NULL) return newNode(sleutel); // Anders ga je terug in de boom als (key< node->sleutel) { knooppunt->links = invoegen(knooppunt->links, sleutel); } else if (sleutel> knooppunt->sleutel) { knooppunt->rechts = insert(knooppunt->rechts, sleutel); } // Retourneer het retourknooppunt van de knooppuntaanwijzer; }> C // Given Node Structure struct node { int key; struct node *left, *right; }; // Function to create a new BST node struct node* newNode(int item) { struct node* temp = (struct node*)malloc( sizeof(struct node)); temp->sleutel = artikel; temp->links = temp->rechts = NULL; retourtemperatuur; } // Functie om een nieuw knooppunt in te voegen met // gegeven sleutel in BST struct node* insert(struct node* node, int key) {// Als de boom leeg is, retourneer dan een nieuw knooppunt if (node == NULL) return newNode(sleutel); // Anders ga je terug in de boom als (key< node->sleutel) { knooppunt->links = invoegen(knooppunt->links, sleutel); } else if (sleutel> knooppunt->sleutel) { knooppunt->rechts = insert(knooppunt->rechts, sleutel); } // Retourneer het retourknooppunt van de knooppuntaanwijzer; }> Java class GFG { // Given Node Structure static class node { int key; node left, right; }; // Function to create a new BST node static node newNode(int item) { node temp = new node(); temp.key = item; temp.left = temp.right = null; return temp; } // Function to insert a new node with // given key in BST static node insert(node node, int key) { // If the tree is empty, return a new node if (node == null) return newNode(key); // Otherwise, recur down the tree if (key < node.key) { node.left = insert(node.left, key); } else if (key>knooppunt.sleutel) { knooppunt.rechts = invoegen(knooppunt.rechts, sleutel); } // Retourneer het knooppunt retourknooppunt; } }> Python3 # Given Node Structure class Node: def __init__(self, key): self.key = key self.left = None self.right = None # Function to insert a new node with # given key in BST def insert(node, key): # If the tree is empty, return a new node if node is None: return Node(key) # Otherwise, recur down the tree if key < node.key: node.left = insert(node.left, key) elif key>node.key: node.right = insert(node.right, key) # Retourneert de knooppuntaanwijzer return node>
Javascript // Given Node Structure class Node { constructor(key){ this.key = key; this.left = null; this.right = null; } } // Function to insert a new node with // given key in BST function insert(node, key) { // If the tree is empty, return a new node if (node == null) return new Node(key); // Otherwise, recur down the tree if (key < node.key) { node.left = insert(node.left, key); } else if (key>knooppunt.sleutel) { knooppunt.rechts = invoegen(knooppunt.rechts, sleutel); } // Retourneer het retourknooppunt van de knooppuntaanwijzer; }> Tijdcomplexiteit: O(N), waarbij N het aantal knooppunten van de BST is
Hulpruimte: O(1)
3. Verwijder een knooppunt van BST :
Het wordt gebruikt om een knooppunt met een specifieke sleutel uit de BST te verwijderen en de nieuwe BST terug te sturen.
Verschillende scenario's voor het verwijderen van het knooppunt:
Java-keuzelijst
Het knooppunt dat moet worden verwijderd, is het bladknooppunt :
Het is eenvoudig, je kunt het gewoon op nul zetten.
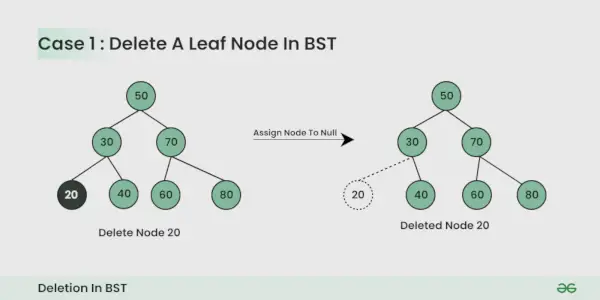
Het te verwijderen knooppunt heeft één onderliggend knooppunt :
U kunt het knooppunt gewoon vervangen door het onderliggende knooppunt.
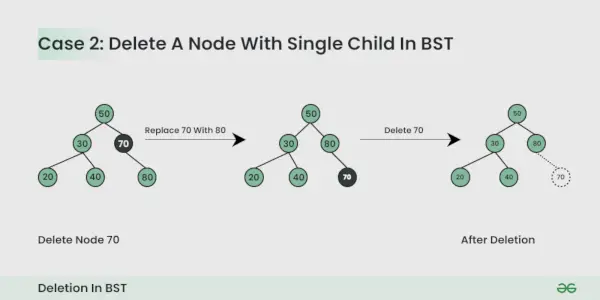
Het te verwijderen knooppunt heeft twee onderliggende knooppunten :
Hier moeten we het verwijderen van het knooppunt is zo dat de resulterende boom de eigenschappen van een BST volgt. De truc is om de niet-geordende opvolger van het knooppunt te vinden. Kopieer de inhoud van de niet-geordende opvolger naar het knooppunt en verwijder de niet-geordende opvolger.
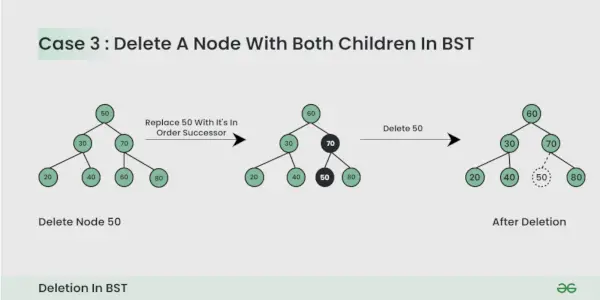
Zorg voor de volgende zaken bij het verwijderen van een knooppunt van een BST:
- Moet uitzoeken wat de vervanging zal zijn van het knooppunt dat moet worden verwijderd.
- Wilt u een minimale verstoring van de bestaande boomstructuur
- Kan het vervangende knooppunt uit de verwijderde knooppunten linker- of rechtersubboom halen.
- Als we if uit de linker deelboom nemen, moeten we de grootste waarde in de linker deelboom nemen.
- Als we if uit de rechter deelboom nemen, moeten we de kleinste waarde in de rechter deelboom nemen.
Code:
Hieronder ziet u de implementatie van de verwijdering in BST:
C++ // C++ program to delete // a node of BST // Given Node node struct node { int key; struct node *left, *right; }; // Function to create a new BST node struct node* newNode(int item) { struct node* temp = (struct node*)malloc( sizeof(struct node)); temp->sleutel = artikel; temp->links = temp->rechts = NULL; retourtemperatuur; } // Functie om een nieuw knooppunt in te voegen met // gegeven sleutel in BST struct node* insert(struct node* node, int key) {// Als de boom leeg is, retourneer dan een nieuw knooppunt if (node == NULL) return newNode(sleutel); // Anders ga je terug in de boom als (key< node->sleutel) { knooppunt->links = invoegen(knooppunt->links, sleutel); } else if (sleutel> knooppunt->sleutel) { knooppunt->rechts = insert(knooppunt->rechts, sleutel); } // Retourneer het retourknooppunt van de knooppuntaanwijzer; } // Functie die het knooppunt retourneert met minimum // sleutelwaarde gevonden in die boom struct node* minValueNode(struct node* node) { struct node* current = node; // Loop naar beneden om het meest linkse blad te vinden terwijl (current && current->left != NULL) current = current->left; retourstroom; } // Functie die de sleutel verwijdert en // retourneert de nieuwe root struct node* deleteNode(struct node* root, int key) {// base Case if (root == NULL) return root; // Als de te verwijderen sleutel // kleiner is dan de sleutel van de root, // dan ligt deze in de linker subboom if (key< root->sleutel) { root->left = deleteNode(root->left, key); } // Als de te verwijderen sleutel // groter is dan de sleutel van de root, // dan ligt deze in de rechter subboom else if (key> root->key) { root->right = deleteNode(root-> rechts, sleutel); } // Als de sleutel hetzelfde is als de sleutel van root, // dan is dit het knooppunt // dat moet worden verwijderd else {/ // Knooppunt met slechts één kind // of geen kind if (root->left == NULL) { struct node* temp = root->rechts; gratis(root); retourtemperatuur; } else if (root->right == NULL) { struct node* temp = root->left; gratis(root); retourtemperatuur; } // Knooppunt met twee kinderen: // Haal de opvolger in de juiste volgorde op (kleinste // in de rechter subboom) struct node* temp = minValueNode(root->right); // Kopieer de // inhoud van de opvolger naar dit knooppunt root->key = temp->key; // Verwijder de opvolger root->right = deleteNode(root->right, temp->key); } return root; }> C // C program to delete // a node of BST // Given Node node struct node { int key; struct node *left, *right; }; // Function to create a new BST node struct node* newNode(int item) { struct node* temp = (struct node*)malloc( sizeof(struct node)); temp->sleutel = artikel; temp->links = temp->rechts = NULL; retourtemperatuur; } // Functie om een nieuw knooppunt in te voegen met // gegeven sleutel in BST struct node* insert(struct node* node, int key) {// Als de boom leeg is, retourneer dan een nieuw knooppunt if (node == NULL) return newNode(sleutel); // Anders ga je terug in de boom als (key< node->sleutel) { knooppunt->links = invoegen(knooppunt->links, sleutel); } else if (sleutel> knooppunt->sleutel) { knooppunt->rechts = insert(knooppunt->rechts, sleutel); } // Retourneer het retourknooppunt van de knooppuntaanwijzer; } // Functie die het knooppunt retourneert met minimum // sleutelwaarde gevonden in die boom struct node* minValueNode(struct node* node) { struct node* current = node; // Loop naar beneden om het meest linkse blad te vinden terwijl (current && current->left != NULL) current = current->left; retourstroom; } // Functie die de sleutel verwijdert en // retourneert de nieuwe root struct node* deleteNode(struct node* root, int key) {// base Case if (root == NULL) return root; // Als de te verwijderen sleutel // kleiner is dan de sleutel van de root, // dan ligt deze in de linker subboom if (key< root->sleutel) { root->left = deleteNode(root->left, key); } // Als de te verwijderen sleutel // groter is dan de sleutel van de root, // dan ligt deze in de rechter subboom else if (key> root->key) { root->right = deleteNode(root-> rechts, sleutel); } // Als de sleutel hetzelfde is als de sleutel van root, // dan is dit het knooppunt // dat moet worden verwijderd else {/ // Knooppunt met slechts één kind // of geen kind if (root->left == NULL) { struct node* temp = root->rechts; gratis(root); retourtemperatuur; } else if (root->right == NULL) { struct node* temp = root->left; gratis(root); retourtemperatuur; } // Knooppunt met twee kinderen: // Haal de opvolger in de juiste volgorde op (kleinste // in de rechter subboom) struct node* temp = minValueNode(root->right); // Kopieer de // inhoud van de opvolger naar dit knooppunt root->key = temp->key; // Verwijder de opvolger root->right = deleteNode(root->right, temp->key); } return root; }> Java // Java program for Delete a Node of BST class GFG { // Given Node node static class node { int key; node left, right; }; // Function to create a new BST node static node newNode(int item) { node temp = new node(); temp.key = item; temp.left = temp.right = null; return temp; } // Function to insert a new node with // given key in BST static node insert(node node, int key) { // If the tree is empty, return a new node if (node == null) return newNode(key); // Otherwise, recur down the tree if (key < node.key) { node.left = insert(node.left, key); } else if (key>knooppunt.sleutel) { knooppunt.rechts = invoegen(knooppunt.rechts, sleutel); } // Retourneer het knooppunt retourknooppunt; } // Functie die het knooppunt retourneert met een minimum // sleutelwaarde gevonden in die boom statisch knooppunt minValueNode(knooppunt) { knooppunt huidig = knooppunt; // Loop naar beneden om het meest linkse blad te vinden terwijl (current != null && current.left != null) current = current.left; retourstroom; } // Functie die de sleutel verwijdert en // het nieuwe statische rootknooppunt retourneert deleteNode(node root, int key) {// base Case if (root == null) return root; // Als de te verwijderen sleutel // kleiner is dan de sleutel van de root, // dan ligt deze in de linker subboom if (key< root.key) { root.left = deleteNode(root.left, key); } // If the key to be deleted is // greater than the root's key, // then it lies in right subtree else if (key>root.key) { root.right = deleteNode(root.right, sleutel); } // Als de sleutel hetzelfde is als de sleutel van root, // dan is dit het knooppunt // dat verwijderd moet worden else {/ // Knooppunt met slechts één kind // of geen kind if (root.left == null) { knooppunttemperatuur = root.right; retourtemperatuur; } else if (root.right == null) { node temp = root.left; retourtemperatuur; } // Knooppunt met twee kinderen: // Haal de in de juiste volgorde opvolgende opvolger (kleinste // in de rechter subboom) knooppunt temp = minValueNode (root.right); // Kopieer de // inhoud van de opvolger naar dit knooppunt root.key = temp.key; // Verwijder de opvolger root.right = deleteNode(root.right, temp.key); } return root; }> Python # Python program to delete a node of BST # Given Node node class Node: def __init__(self, key): self.key = key self.left = None self.right = None # Function to insert a new node with # given key in BST def insert(root, key): # If the tree is empty, return a new node if root is None: return Node(key) # Otherwise, recur down the tree if key < root.key: root.left = insert(root.left, key) elif key>root.key: root.right = insert(root.right, key) # Retourneert de knooppuntaanwijzer return root # Functie die moet worden uitgevoerd in volgorde van BST def inorder(root): if root: inorder(root.left) print(root. key, end=' ') inorder(root.right) # Functie die het knooppunt retourneert met minimum # sleutelwaarde gevonden in die boom def minValueNode(node): current = node # Loop naar beneden om het meest linkse blad te vinden terwijl dit actueel is en current.left is niet Geen: current = current.left return current # Functie die de sleutel verwijdert en # retourneert de nieuwe root def deleteNode(root, key): # basisgeval als root Geen is: return root # Als de sleutel moet zijn verwijderd is # kleiner dan de sleutel van de root, # en ligt dan in de linker subboom als sleutel< root.key: root.left = deleteNode(root.left, key) # If the key to be deleted is # greater than the root's key, # then it lies in right subtree elif key>root.key: root.right = deleteNode(root.right, key) # Als de sleutel hetzelfde is als de sleutel van root, # dan is dit het # knooppunt dat verwijderd moet worden, anders: # Knooppunt met slechts één kind # of geen kind als root.left Geen is: temp = root.right root = Geen return temp elif root.right is Geen: temp = root.left root = Geen return temp # Knooppunt met twee kinderen: # Haal de in volgorde opvolgende opvolger op (kleinste # in de rechter subboom) temp = minValueNode(root.right) # Kopieer de # inhoud van de niet-geordende opvolger naar dit knooppunt root.key = temp.key # Verwijder de niet-geordende opvolger root.right = deleteNode(root.right, temp.key) retourneer root>
4. Traversal (in volgorde van BST) :
In het geval van binaire zoekbomen (BST) geeft Inorder-traversal knooppunten in niet-afnemende volgorde. We bezoeken eerst het linkerkind, dan de wortel en dan het rechterkind.
Hieronder vindt u de implementatie van hoe u een binaire zoekboom in volgorde kunt doorlopen:
C++ // C++ program to implement // inorder traversal of BST #include using namespace std; // Given Node node struct node { int key; struct node *left, *right; }; // Function to create a new BST node struct node* newNode(int item) { struct node* temp = (struct node*)malloc( sizeof(struct node)); temp->sleutel = artikel; temp->links = temp->rechts = NULL; retourtemperatuur; } // Functie om een nieuw knooppunt in te voegen met // gegeven sleutel in BST struct node* insert(struct node* node, int key) {// Als de boom leeg is, retourneer dan een nieuw knooppunt if (node == NULL) return newNode(sleutel); // Anders ga je terug in de boom als (key< node->sleutel) { knooppunt->links = invoegen(knooppunt->links, sleutel); } else if (sleutel> knooppunt->sleutel) { knooppunt->rechts = insert(knooppunt->rechts, sleutel); } // Retourneer het retourknooppunt van de knooppuntaanwijzer; } // Functie voor het doorlopen van BST void inorder(struct node* root) { if (root != NULL) { inorder(root->left); uit<< ' ' << root->sleutel; inorder(wortel->rechts); } } // Stuurprogrammacode int main() { /* Laten we de volgende BST 50 / 30 70 / / 20 40 60 80 */ struct node* root = NULL maken; // De BST-root aanmaken = insert(root, 50); invoegen(wortel, 30); invoegen(wortel, 20); invoegen(wortel, 40); invoegen(wortel, 70); invoegen(wortel, 60); invoegen(wortel, 80); // Functieoproep in volgorde (root); retour 0; } // Deze code is bijgedragen door shivanisinghss2110> C // C program to implement // inorder traversal of BST #include #include // Given Node node struct node { int key; struct node *left, *right; }; // Function to create a new BST node struct node* newNode(int item) { struct node* temp = (struct node*)malloc( sizeof(struct node)); temp->sleutel = artikel; temp->links = temp->rechts = NULL; retourtemperatuur; } // Functie om een nieuw knooppunt in te voegen met // gegeven sleutel in BST struct node* insert(struct node* node, int key) {// Als de boom leeg is, retourneer dan een nieuw knooppunt if (node == NULL) return newNode(sleutel); // Anders ga je terug in de boom als (key< node->sleutel) { knooppunt->links = invoegen(knooppunt->links, sleutel); } else if (sleutel> knooppunt->sleutel) { knooppunt->rechts = insert(knooppunt->rechts, sleutel); } // Retourneer het retourknooppunt van de knooppuntaanwijzer; } // Functie voor het doorlopen van BST void inorder(struct node* root) { if (root != NULL) { inorder(root->left); printf('%d ', root->sleutel); inorder(wortel->rechts); } } // Stuurprogrammacode int main() { /* Laten we de volgende BST 50 / 30 70 / / 20 40 60 80 */ struct node* root = NULL maken; // De BST-root aanmaken = insert(root, 50); invoegen(wortel, 30); invoegen(wortel, 20); invoegen(wortel, 40); invoegen(wortel, 70); invoegen(wortel, 60); invoegen(wortel, 80); // Functieoproep in volgorde (root); retour 0; }> Java import java.io.*; // Java program for Inorder Traversal class GFG { // Given Node node static class node { int key; node left, right; }; // Function to create a new BST node static node newNode(int item) { node temp = new node(); temp.key = item; temp.left = temp.right = null; return temp; } // Function to insert a new node with // given key in BST static node insert(node node, int key) { // If the tree is empty, return a new node if (node == null) return newNode(key); // Otherwise, recur down the tree if (key < node.key) { node.left = insert(node.left, key); } else if (key>knooppunt.sleutel) { knooppunt.rechts = invoegen(knooppunt.rechts, sleutel); } // Retourneer het knooppunt retourknooppunt; } // Functie om de statische leegte van BST in volgorde te doorlopen (node root) { if (root != null) { inorder (root.left); Systeem.out.print(' ' + root.key); inorder(root.right); } } // Stuurprogrammacode public static void main(String[] args) { /* Laten we de volgende BST 50 / 30 70 / / 20 40 60 80 */ node root = null maken; // waarde invoegen 50 root = insert(root, 50); // waarde invoegen 30 insert(root, 30); // waarde invoegen 20 insert(root, 20); // waarde invoegen 40 insert(root, 40); // waarde invoegen 70 insert(root, 70); // waarde invoegen 60 insert(root, 60); // waarde invoegen 80 insert(root, 80); // druk de BST af in volgorde (root); } } // Deze code is bijgedragen door abhijitjadhav1998> Python3 # Python program to implement # inorder traversal of BST # Given Node node class Node: def __init__(self, key): self.key = key self.left = None self.right = None # Function to create a new BST node def newNode(item): temp = Node(item) temp.key = item temp.left = temp.right = None return temp # Function to insert a new node with # given key in BST def insert(node, key): # If the tree is empty, return a new node if node is None: return newNode(key) # Otherwise, recur down the tree if key < node.key: node.left = insert(node.left, key) elif key>node.key: node.right = insert(node.right, key) # Retourneert de knooppuntaanwijzer return node # Functie die moet worden uitgevoerd in volgorde van BST def inorder(root): if root: inorder(root.left) print(root. key, end=' ') inorder(root.right) # Stuurprogrammacode if __name__ == '__main__': # Laten we de volgende BST maken # 50 # / # 30 70 # / / # 20 40 60 80 root = Geen # De BST-root aanmaken = insert(root, 50) insert(root, 30) insert(root, 20) insert(root, 40) insert(root, 70) insert(root, 60) insert(root , 80) # Functieaanroep inorder(root) #Deze code is bijgedragen door japmeet01>
Uitvoer
20 30 40 50 60 70 80>
Tijdcomplexiteit: O(N), waarbij N het aantal knooppunten van de BST is
Hulpruimte: O(1)
Toepassingen van BST:
- Grafiekalgoritmen: BST's kunnen worden gebruikt om grafiekalgoritmen te implementeren, zoals in minimum spanning tree-algoritmen.
- Prioritaire wachtrijen: BST's kunnen worden gebruikt om prioriteitswachtrijen te implementeren, waarbij het element met de hoogste prioriteit zich in de wortel van de boom bevindt en elementen met een lagere prioriteit in de subbomen worden opgeslagen.
- Zelfbalancerende binaire zoekboom: BST's kunnen worden gebruikt als zelfbalancerende datastructuren zoals AVL-boom en rood-zwarte boom.
- Gegevensopslag en ophalen: BST's kunnen worden gebruikt om gegevens snel op te slaan en op te halen, bijvoorbeeld in databases, waar in logaritmische tijd naar een specifiek record kan worden gezocht.
Voordelen:
- Snel zoeken: Het zoeken naar een specifieke waarde in een BST heeft een gemiddelde tijdscomplexiteit van O(log n), waarbij n het aantal knooppunten in de boom is. Dit is veel sneller dan het zoeken naar een element in een array of gekoppelde lijst, die in het ergste geval een tijdscomplexiteit van O(n) hebben.
- In volgorde doorlopen: BST's kunnen in volgorde worden doorlopen, waarbij de linker subboom, de root en de rechter subboom worden bezocht. Dit kan worden gebruikt om een dataset te sorteren.
- Ruimtebesparend: BST's zijn ruimtebesparend omdat ze geen redundante informatie opslaan, in tegenstelling tot arrays en gekoppelde lijsten.
Nadelen:
- Scheve bomen: Als een boom scheef raakt, zal de tijdscomplexiteit van zoek-, invoeg- en verwijderbewerkingen O(n) zijn in plaats van O(log n), wat de boom inefficiënt kan maken.
- Extra benodigde tijd: Zelfbalancerende bomen hebben extra tijd nodig om het evenwicht te bewaren tijdens het inbrengen en verwijderen.
- Efficiëntie: BST's zijn niet efficiënt voor datasets met veel duplicaten, omdat ze ruimte verspillen.
Veelgestelde vragen(Veel Gestelde Vragen)op binaire zoekboom:
1. Wat is een binaire zoekboom?
Een binaire zoekboom (BST) is een binaire boom waarbij elk knooppunt in de linker deelboom kleiner is dan de wortel, en elk knooppunt in de rechter deelboom een waarde heeft die groter is dan de wortel . De eigenschappen van een binaire zoekboom zijn recursief: als we een knooppunt als wortel beschouwen, blijven deze eigenschappen waar.
2. Wat is de binaire zoekboombewerking?
Er zijn drie belangrijke bewerkingen in de binaire zoekboom: 1. Invoegen, 2. Verwijderen, 3. Zoeken. Vanwege zijn eigenschappen is het efficiënt om elk element in de binaire zoekboom te doorzoeken.
3. Wat is de binaire zoekboom en de AVL-boom?
Binaire zoekboom : Een binaire zoekboom (BST) is een binaire boom waarbij elk knooppunt in de linker deelboom kleiner is dan de wortel, en elk knooppunt in de rechter deelboom een waarde heeft die groter is dan de wortel.
AVL-boom : Binaire zoekbomen (BST's) die zichzelf in evenwicht brengen en automatisch roteren, staan bekend als AVL-bomen.
4. Wat zijn de toepassingen van de binaire zoekboom?
Binaire zoekbomen kunnen worden gebruikt om abstracte gegevenstypen te implementeren, zoals dynamische sets, opzoektabellen en prioriteitswachtrijen, en erin gebruikt sorteeralgoritmen zoals boomsoort.
5. Wat is het verschil tussen binaire zoekboom en binaire boom?
Een binaire zoekboom is een boom die een bepaalde volgorde volgt om de elementen te rangschikken, terwijl de binaire boom geen enkele volgorde volgt.
Gerelateerde artikelen:
- Toepassing van BST
- Toepassingen, voordelen en nadelen van binaire zoekboom
- Invoeging in binaire zoekboom (BST)
- Zoeken in binaire zoekboom (BST)
- Verwijdering in binaire zoekboom (BST)
