A Balie is een apparaat dat het aantal keren dat een bepaalde gebeurtenis of proces heeft plaatsgevonden opslaat (en soms weergeeft), vaak in relatie tot een kloksignaal. Tellers worden in de digitale elektronica gebruikt voor teldoeleinden, ze kunnen specifieke gebeurtenissen in het circuit tellen. In UP-teller verhoogt een teller bijvoorbeeld het aantal voor elke stijgende flank van de klok. Een teller kan niet alleen tellen, maar kan ook een bepaalde volgorde volgen op basis van ons ontwerp, zoals elke willekeurige reeks 0,1,3,2…. Ze kunnen ook worden ontworpen met behulp van flip-flops. Ze worden gebruikt als frequentiedelers waarbij de frequentie van een bepaalde pulsgolfvorm wordt verdeeld. Tellers zijn sequentiële circuits die het aantal pulsen tellen, zowel in binaire code als in BCD-vorm. De belangrijkste eigenschappen van een teller zijn timing, opeenvolging en tellen. Teller werkt in twee modi
Teller omhoog
Omlaag teller
Tegenclassificatie
Tellers zijn grofweg verdeeld in twee categorieën
- Asynchrone teller
- Synchrone teller
1. Asynchrone teller
In een asynchrone teller gebruiken we geen universele klok, alleen de eerste flip-flop wordt aangedreven door de hoofdklok en de klokinvoer van de rest van de volgende flip-flop wordt aangedreven door de uitvoer van eerdere flip-flops. We kunnen het begrijpen door het volgende diagram te volgen:
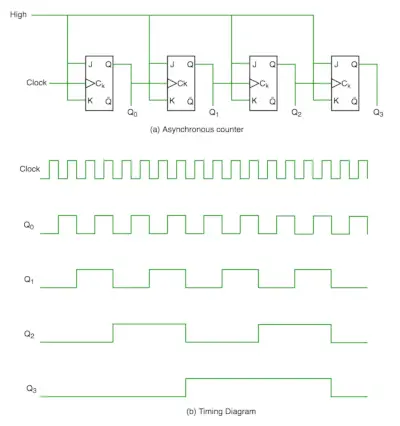
Uit het timingdiagram blijkt duidelijk dat Q0 verandert zodra de stijgende flank van de klokpuls wordt tegengekomen, Q1 verandert wanneer de stijgende flank van Q0 wordt tegengekomen (omdat Q0 lijkt op de klokpuls voor de tweede flip-flop), enzovoort. Op deze manier worden rimpelingen gegenereerd via Q0,Q1,Q2,Q3, vandaar dat het ook wel wordt genoemd RIPPLE-teller en seriële teller. Een rimpelteller is een cascadeschakeling van flip-flops waarbij de uitgang van de ene flip-flop de klokingang van de volgende flip-flop aanstuurt
2. Synchrone teller
In tegenstelling tot de asynchrone teller heeft de synchrone teller één globale klok die elke flip-flop aanstuurt, zodat de uitvoer parallel verandert. Het enige voordeel van een synchrone teller ten opzichte van een asynchrone teller is dat deze op een hogere frequentie kan werken dan een asynchrone teller, omdat deze geen cumulatieve vertraging heeft omdat aan elke flip-flop dezelfde klok wordt gegeven. Het wordt ook wel een parallelle teller genoemd.
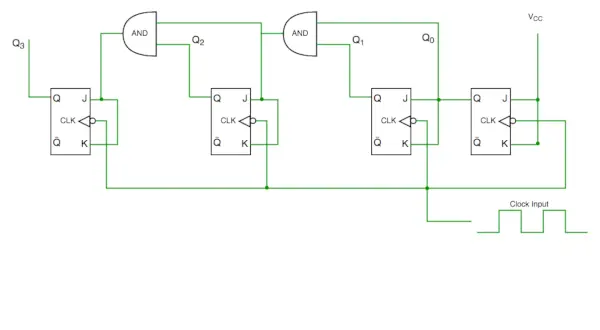
Synchrone tellerschakeling
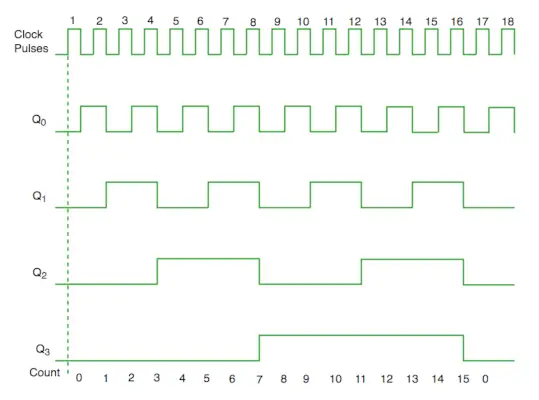
Timingdiagram synchrone teller
Uit het schakelschema zien we dat Q0 bit antwoord geeft op elke dalende flank van de klok, terwijl Q1 afhankelijk is van Q0, Q2 afhankelijk is van Q1 en Q0, Q3 afhankelijk is van Q2, Q1 en Q0.
Decennium teller
Een decenniumteller telt tien verschillende toestanden en wordt vervolgens teruggezet naar de oorspronkelijke toestanden. Een eenvoudige decadeteller telt van 0 tot 9, maar we kunnen ook decadetellers maken die door elke tien toestanden tussen 0 en 15 kunnen gaan (voor een 4-bits teller).
| Klokpuls | Q3 | Vraag 2 | Q1 | Q0 |
| 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 1 |
| 2 | 0 | 0 | 1 | 0 |
| 3 | 0 | 0 | 1 | 1 |
| 4 | 0 | 1 | 0 | 0 |
| 5 | 0 | 1 | 0 | 1 |
| 6 | 0 | 1 | 1 | 0 |
| 7 | 0 | 1 | 1 | 1 |
| 8 | 1 | 0 | 0 | 0 |
| 9 | 1 | 0 | 0 | 1 |
| 10 | 0 | 0 | 0 | 0 |
Waarheidstabel voor eenvoudige decenniateller
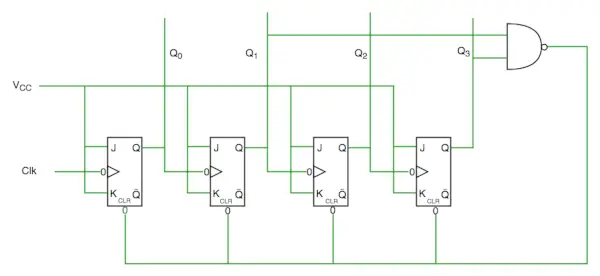
Decenniumteller schakelschema
We zien aan het schakelschema dat we nand-poort hebben gebruikt voor Q3 en Q1 en deze hebben ingevoerd om de invoerlijn te wissen, omdat de binaire representatie van 10 is:
1010
En we zien dat Q3 en Q1 hier 1 zijn, als we NAND van deze twee bits geven om de invoer te wissen, dan zal de teller leeg zijn op 10 en opnieuw beginnen vanaf het begin.
Belangrijk punt : Het aantal flipflops dat in de teller wordt gebruikt, is altijd groter dan gelijk aan ( loggen2N ) waarbij n=aantal toestanden in de teller.
Sommige voorgaande jaren hebben vragen over tellers
Q1. Beschouw de gedeeltelijke implementatie van een 2-bits teller met behulp van T-flip-flops volgens de reeks 0-2-3-1-0, zoals hieronder weergegeven
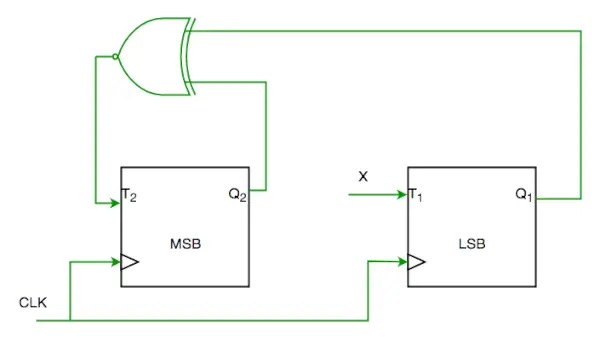
Om het circuit te voltooien, moet de ingang X zijn
(A) Vraag 2?
(B) Q2 + Q1
(C) (Q1? Q2)’
(D) Q1? Vraag 2 (POORT-CS-2004)
Oplossing:
Van circuit zien we
T1=XQ1’+X’Q1—-(1)
EN
T2=(Q2 ? Q1)’—-(2)
EN DE GEWENSTE UITGANG IS 00->10->11->01->00
DUS MOET X ZIJN Q1Q2’+Q1’Q2 BEVREDIGEND 1 EN 2.
DUS ANS IS (D) DEEL.
Vraag 2. De stuursignaalfuncties van een 4-bits binaire teller worden hieronder gegeven (waarbij X 'maakt niet uit')
De teller is als volgt aangesloten:
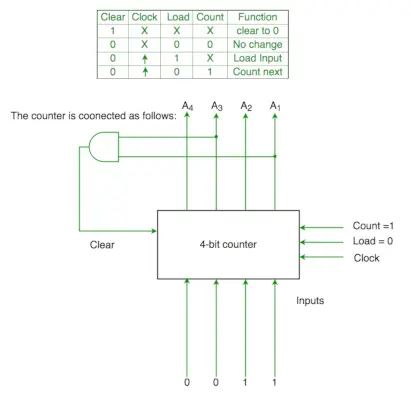
Neem aan dat de teller- en poortvertragingen verwaarloosbaar zijn. Als de teller op 0 begint, doorloopt deze de volgende reeks:
(A) 0,3,4
(B) 0,3,4,5
(C) 0,1,2,3,4
(D) 0,1,2,3,4,5 (POORT-CS-2007)
Oplossing:
Aanvankelijk A1 A2 A3 A4 =0000
Clr=A1 en A3
Dus als A1 en A3 beide 1 zijn, gaat het opnieuw naar 0000
Vandaar 0000(init.) -> 0001(A1 en A3=0) ->0010 (A1 en A3=0) -> 0011(A1 en A3=0) -> 0100 ( A1 en A3=1 )[ duidelijke voorwaarde voldaan] ->0000(init.) dus het gaat door 0->1->2->3->4
Ans is (C) onderdeel.
toetsenbord voor pagina omlaag
Quiz over digitale logica
Artikel bijgedragen door Anuj Batham,
