
Gegeven een verbonden ongerichte grafiek vertegenwoordigd door een aangrenzende lijst adjLijst[][] met N knooppunten en M randen waarbij elk knooppunt een apart etiket van 0 tot n-1 en elke adj[i] vertegenwoordigt de lijst met hoekpunten die zijn verbonden met hoekpunt i.
Maak een kloon van de grafiek waarbij elk knooppunt in de grafiek een geheel getal bevat val en een array ( buren ) van knooppunten met knooppunten die grenzen aan het huidige knooppunt.
vlc om YouTube-video's te downloaden
klasse knooppunt {
waarde: geheel getal
buren: Lijst[Node]
}
Jouw taak is om de gegeven grafiek te klonen en een verwijzing naar de gekloonde grafiek terug te geven.
Opmerking: Als u een correcte kopie van de gegeven grafiek retourneert, zal de uitvoer waar zijn; anders wordt de kopie vals afgedrukt als de kopie onjuist is.
Voorbeelden
Invoer: n = 4 adjLijst[][] = [[1 2] [0 2] [0 1 3] [2]]
Uitgang: WAAR
Uitleg:
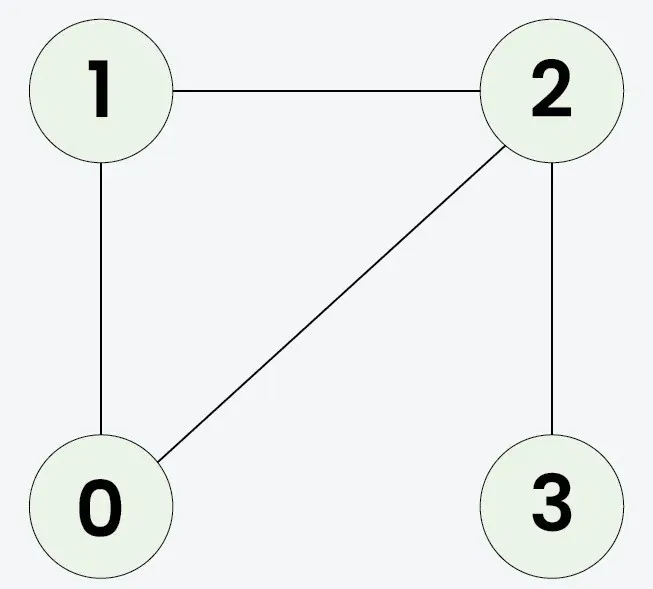
Omdat de gekloonde grafiek identiek is aan het origineel, zal de uitvoer waar zijn.Invoer: n = 3 adjLijst[][] = [[1 2] [0] [0]]
Uitgang: WAAR
Uitleg:
Omdat de gekloonde grafiek identiek is aan het origineel, zal de uitvoer waar zijn.
Inhoudsopgave
- Waarom moeten we de bezochte/gekloonde knooppunten volgen?
- Hoe kan ik de bezochte/gekloonde knooppunten bijhouden?
- Hoe kloonknooppunten verbinden?
- Hoe controleer ik of de gekloonde grafiek correct is?
- [Aanpak 1] BFS-traversal gebruiken - O(V+E) tijd en O(V) ruimte
- [Aanpak 2] DFS-traversal gebruiken - O(V+E) tijd en O(V) ruimte
Waarom moeten we de bezochte/gekloonde knooppunten volgen?
We moeten bezochte of gekloonde knooppunten volgen om oneindige recursie en overtollig werk bij het klonen van een grafiek te voorkomen. Omdat grafieken cycli kunnen bevatten (waarbij een knooppunt terug kan verwijzen naar een eerder bezocht knooppunt) zonder de knooppunten bij te houden die we al hebben gekloond, zou de kloonfunctie eindeloos dezelfde knooppunten opnieuw bezoeken, wat resulteert in een stapeloverloop of onjuiste duplicatie.
Hoe kan ik de bezochte/gekloonde knooppunten bijhouden?
Een HashMap/Map is vereist om alle knooppunten te behouden die al zijn gemaakt. Sleutelwinkels : Referentie/adres van origineel knooppunt Waardewinkels : Referentie/adres van gekloond knooppunt Er is een kopie gemaakt van alle grafiekknooppunten.
Hoe kloonknooppunten verbinden?
Tijdens een bezoek aan de aangrenzende hoekpunten van a knooppunt in krijg de overeenkomstige gekloonde knooppunt voor jou, laten we dat noemen IN Bezoek nu alle aangrenzende knooppunten voor in en zoek voor elke buur het corresponderende kloonknooppunt (indien niet gevonden, maak er een) en duw dan in de aangrenzende vector van IN knooppunt.
Hoe controleer ik of de gekloonde grafiek correct is?
Voer een BFS-doorgang uit op de originele grafiek vóór het klonen en vervolgens opnieuw op de gekloonde grafiek nadat het klonen is voltooid. Tijdens elke doorgang wordt de waarde van elk knooppunt afgedrukt, samen met zijn adres (of referentie). Om de juistheid van het klonen te verifiëren, vergelijkt u de volgorde van de knooppunten die tijdens beide traversals worden bezocht. Als de knooppuntwaarden in dezelfde volgorde verschijnen, maar hun adressen (of referenties) verschillen, bevestigt dit dat de grafiek succesvol en correct is gekloond.
inkapseling programma
Ontdek hoe kloon een ongerichte grafiek, inclusief grafieken met meerdere verbonden componenten met behulp van BFS of DFS om een volledige diepe kopie van alle knooppunten en randen te garanderen.
[Aanpak 1] BFS-traversal gebruiken - O(V+E) tijd en O(V) ruimte
C++Bij de BFS-benadering wordt de grafiek iteratief gekloond met behulp van een wachtrij. We beginnen met het klonen van het initiële knooppunt en het in de wachtrij plaatsen. Terwijl we elk knooppunt uit de wachtrij verwerken, bezoeken we de buren. Als een buurman nog niet is gekloond, maken we een kloon, slaan deze op een kaart op en zetten deze in de wachtrij voor latere verwerking. Vervolgens voegen we de kloon van de buur toe aan de kloonlijst van het huidige knooppunt. Dit proces gaat niveau voor niveau verder en zorgt ervoor dat alle knooppunten in de breedte-eerste volgorde worden bezocht. BFS is vooral handig om diepe recursie te vermijden en grote of brede grafieken efficiënt te verwerken.
#include
import java.util.*; // Definition for a Node class Node { public int val; public ArrayList<Node> neighbors; public Node() { neighbors = new ArrayList<>(); } public Node(int val) { this.val = val; neighbors = new ArrayList<>(); } } public class GfG { // Clone the graph public static Node cloneGraph(Node node) { if (node == null) return null; Map<Node Node> mp = new HashMap<>(); Queue<Node> q = new LinkedList<>(); // Clone the starting node Node clone = new Node(node.val); mp.put(node clone); q.offer(node); while (!q.isEmpty()) { Node current = q.poll(); for (Node neighbor : current.neighbors) { // Clone neighbor if it hasn't been cloned yet if (!mp.containsKey(neighbor)) { mp.put(neighbor new Node(neighbor.val)); q.offer(neighbor); } // Add the clone of the neighbor to the current node's clone mp.get(current).neighbors.add(mp.get(neighbor)); } } return mp.get(node); } // Build graph public static Node buildGraph() { Node node1 = new Node(0); Node node2 = new Node(1); Node node3 = new Node(2); Node node4 = new Node(3); node1.neighbors.addAll(new ArrayList<> (Arrays.asList(node2 node3))); node2.neighbors.addAll(new ArrayList<> (Arrays.asList(node1 node3))); node3.neighbors.addAll(new ArrayList<> (Arrays.asList(node1 node2 node4))); node4.neighbors.addAll(new ArrayList<> (Arrays.asList(node3))); return node1; } // Compare two graphs for structure and value public static boolean compareGraphs(Node n1 Node n2 HashMap<Node Node> visited) { if (n1 == null || n2 == null) return n1 == n2; if (n1.val != n2.val || n1 == n2) return false; visited.put(n1 n2); if (n1.neighbors.size() != n2.neighbors.size()) return false; for (int i = 0; i < n1.neighbors.size(); i++) { Node neighbor1 = n1.neighbors.get(i); Node neighbor2 = n2.neighbors.get(i); if (visited.containsKey(neighbor1)) { if (visited.get(neighbor1) != neighbor2) return false; } else { if (!compareGraphs(neighbor1 neighbor2 visited)) return false; } } return true; } public static void main(String[] args) { Node original = buildGraph(); Node cloned = cloneGraph(original); boolean isEqual = compareGraphs(original cloned new HashMap<>()); System.out.println(isEqual ? 'true' : 'false'); } }
from collections import deque # Definition for a Node class Node: def __init__(self val=0): self.val = val self.neighbors = [] # Clone the graph def cloneGraph(node): if not node: return None # Map to hold original nodes as keys and their clones as values mp = {} # Initialize BFS queue q = deque([node]) # Clone the starting node mp[node] = Node(node.val) while q: current = q.popleft() for neighbor in current.neighbors: # If neighbor not cloned yet if neighbor not in mp: mp[neighbor] = Node(neighbor.val) q.append(neighbor) # Link clone of neighbor to the clone of the current node mp[current].neighbors.append(mp[neighbor]) return mp[node] # Build graph def buildGraph(): node1 = Node(0) node2 = Node(1) node3 = Node(2) node4 = Node(3) node1.neighbors = [node2 node3] node2.neighbors = [node1 node3] node3.neighbors = [node1 node2 node4] node4.neighbors = [node3] return node1 # Compare two graphs structurally and by values def compareGraphs(n1 n2 visited): if not n1 or not n2: return n1 == n2 if n1.val != n2.val or n1 is n2: return False visited[n1] = n2 if len(n1.neighbors) != len(n2.neighbors): return False for i in range(len(n1.neighbors)): neighbor1 = n1.neighbors[i] neighbor2 = n2.neighbors[i] if neighbor1 in visited: if visited[neighbor1] != neighbor2: return False else: if not compareGraphs(neighbor1 neighbor2 visited): return False return True # Driver if __name__ == '__main__': original = buildGraph() cloned = cloneGraph(original) result = compareGraphs(original cloned {}) print('true' if result else 'false')
using System; using System.Collections.Generic; // Definition for a Node public class Node { public int val; public List<Node> neighbors; public Node() { neighbors = new List<Node>(); } public Node(int val) { this.val = val; neighbors = new List<Node>(); } } class GfG { // Clone the graph public static Node CloneGraph(Node node) { if (node == null) return null; var mp = new Dictionary<Node Node>(); var q = new Queue<Node>(); // Clone the starting node var clone = new Node(node.val); mp[node] = clone; q.Enqueue(node); while (q.Count > 0) { var current = q.Dequeue(); foreach (var neighbor in current.neighbors) { // If neighbor not cloned clone it and enqueue if (!mp.ContainsKey(neighbor)) { mp[neighbor] = new Node(neighbor.val); q.Enqueue(neighbor); } // Add clone of neighbor to clone of current mp[current].neighbors.Add(mp[neighbor]); } } return mp[node]; } // Build graph public static Node BuildGraph() { var node1 = new Node(0); var node2 = new Node(1); var node3 = new Node(2); var node4 = new Node(3); node1.neighbors.AddRange(new[] { node2 node3 }); node2.neighbors.AddRange(new[] { node1 node3 }); node3.neighbors.AddRange(new[] { node1 node2 node4 }); node4.neighbors.AddRange(new[] { node3 }); return node1; } // Compare two graphs for structure and value public static bool CompareGraphs(Node n1 Node n2 Dictionary<Node Node> visited) { if (n1 == null || n2 == null) return n1 == n2; if (n1.val != n2.val || ReferenceEquals(n1 n2)) return false; visited[n1] = n2; if (n1.neighbors.Count != n2.neighbors.Count) return false; for (int i = 0; i < n1.neighbors.Count; i++) { var neighbor1 = n1.neighbors[i]; var neighbor2 = n2.neighbors[i]; if (visited.ContainsKey(neighbor1)) { if (!ReferenceEquals(visited[neighbor1] neighbor2)) return false; } else { if (!CompareGraphs(neighbor1 neighbor2 visited)) return false; } } return true; } public static void Main() { var original = BuildGraph(); var cloned = CloneGraph(original); var visited = new Dictionary<Node Node>(); Console.WriteLine(CompareGraphs(original cloned visited) ? 'true' : 'false'); } }
// Definition for a Node class Node { constructor(val = 0) { this.val = val; this.neighbors = []; } } // Clone the graph function cloneGraph(node) { if (!node) return null; const mp = new Map(); const q = [node]; // Clone the initial node mp.set(node new Node(node.val)); while (q.length > 0) { const current = q.shift(); for (const neighbor of current.neighbors) { if (!mp.has(neighbor)) { mp.set(neighbor new Node(neighbor.val)); q.push(neighbor); } // Link clone of neighbor to clone of current mp.get(current).neighbors.push(mp.get(neighbor)); } } return mp.get(node); } // Build graph function buildGraph() { const node1 = new Node(0); const node2 = new Node(1); const node3 = new Node(2); const node4 = new Node(3); node1.neighbors = [node2 node3]; node2.neighbors = [node1 node3]; node3.neighbors = [node1 node2 node4]; node4.neighbors = [node3]; return node1; } // Compare two graphs structurally and by value function compareGraphs(n1 n2 visited = new Map()) { if (!n1 || !n2) return n1 === n2; if (n1.val !== n2.val || n1 === n2) return false; visited.set(n1 n2); if (n1.neighbors.length !== n2.neighbors.length) return false; for (let i = 0; i < n1.neighbors.length; i++) { const neighbor1 = n1.neighbors[i]; const neighbor2 = n2.neighbors[i]; if (visited.has(neighbor1)) { if (visited.get(neighbor1) !== neighbor2) return false; } else { if (!compareGraphs(neighbor1 neighbor2 visited)) return false; } } return true; } // Driver const original = buildGraph(); const cloned = cloneGraph(original); const result = compareGraphs(original cloned); console.log(result ? 'true' : 'false');
Uitvoer
true
[Aanpak 2] DFS-traversal gebruiken - O(V+E) tijd en O(V) ruimte
C++Bij de DFS-benadering wordt de grafiek gekloond met behulp van recursie. We vertrekken vanaf het gegeven knooppunt en verkennen zo ver mogelijk langs elke tak voordat we teruggaan. Er wordt een kaart (of woordenboek) gebruikt om reeds gekloonde knooppunten bij te houden om te voorkomen dat hetzelfde knooppunt meerdere keren wordt verwerkt en om cycli af te handelen. Wanneer we een knooppunt voor de eerste keer tegenkomen, maken we er een kloon van en slaan deze op de kaart op. Vervolgens klonen we het voor elke buur van dat knooppunt recursief en voegen we de gekloonde buur toe aan de kloon van het huidige knooppunt. Dit zorgt ervoor dat alle knooppunten diep worden bezocht voordat ze terugkeren en dat de grafiekstructuur getrouw wordt gekopieerd.
#include
import java.util.*; // Definition for a Node class Node { int val; ArrayList<Node> neighbors; Node() { neighbors = new ArrayList<>(); } Node(int val) { this.val = val; neighbors = new ArrayList<>(); } } public class GfG { // Map to hold original node to its copy static HashMap<Node Node> copies = new HashMap<>(); // Function to clone the graph using DFS public static Node cloneGraph(Node node) { // If the node is NULL return NULL if (node == null) return null; // If node is not yet cloned clone it if (!copies.containsKey(node)) { Node clone = new Node(node.val); copies.put(node clone); // Recursively clone neighbors for (Node neighbor : node.neighbors) { clone.neighbors.add(cloneGraph(neighbor)); } } // Return the clone return copies.get(node); } // Build graph public static Node buildGraph() { Node node1 = new Node(0); Node node2 = new Node(1); Node node3 = new Node(2); Node node4 = new Node(3); node1.neighbors.addAll(Arrays.asList(node2 node3)); node2.neighbors.addAll(Arrays.asList(node1 node3)); node3.neighbors.addAll(Arrays.asList(node1node2 node4)); node4.neighbors.addAll(Arrays.asList(node3)); return node1; } // Compare two graphs for structural and value equality public static boolean compareGraphs(Node node1 Node node2 HashMap<Node Node> visited) { if (node1 == null || node2 == null) return node1 == node2; if (node1.val != node2.val || node1 == node2) return false; visited.put(node1 node2); if (node1.neighbors.size() != node2.neighbors.size()) return false; for (int i = 0; i < node1.neighbors.size(); i++) { Node n1 = node1.neighbors.get(i); Node n2 = node2.neighbors.get(i); if (visited.containsKey(n1)) { if (visited.get(n1) != n2) return false; } else { if (!compareGraphs(n1 n2 visited)) return false; } } return true; } // Driver Code public static void main(String[] args) { Node original = buildGraph(); // Clone the graph Node cloned = cloneGraph(original); // Compare original and cloned graph boolean result = compareGraphs(original cloned new HashMap<>()); System.out.println(result ? 'true' : 'false'); } }
# Definition for a Node class Node: def __init__(self val=0 neighbors=None): self.val = val self.neighbors = neighbors if neighbors is not None else [] # Map to hold original node to its copy copies = {} # Function to clone the graph def cloneGraph(node): # If the node is None return None if not node: return None # If node is not yet cloned clone it if node not in copies: # Create a clone of the node clone = Node(node.val) copies[node] = clone # Recursively clone neighbors for neighbor in node.neighbors: clone.neighbors.append(cloneGraph(neighbor)) # Return the clone return copies[node] def buildGraph(): node1 = Node(0) node2 = Node(1) node3 = Node(2) node4 = Node(3) node1.neighbors = [node2 node3] node2.neighbors = [node1 node3] node3.neighbors = [node1 node2 node4] node4.neighbors = [node3] return node1 # Compare two graphs for structural and value equality def compareGraphs(node1 node2 visited): if not node1 or not node2: return node1 == node2 if node1.val != node2.val or node1 is node2: return False visited[node1] = node2 if len(node1.neighbors) != len(node2.neighbors): return False for i in range(len(node1.neighbors)): n1 = node1.neighbors[i] n2 = node2.neighbors[i] if n1 in visited: if visited[n1] != n2: return False else: if not compareGraphs(n1 n2 visited): return False return True # Driver Code if __name__ == '__main__': original = buildGraph() # Clone the graph using DFS cloned = cloneGraph(original) # Compare original and cloned graph visited = {} print('true' if compareGraphs(original cloned visited) else 'false')
using System; using System.Collections.Generic; public class Node { public int val; public List<Node> neighbors; public Node() { val = 0; neighbors = new List<Node>(); } public Node(int _val) { val = _val; neighbors = new List<Node>(); } } class GfG { // Dictionary to hold original node to its copy static Dictionary<Node Node> copies = new Dictionary<Node Node>(); // Function to clone the graph using DFS public static Node CloneGraph(Node node) { // If the node is NULL return NULL if (node == null) return null; // If node is not yet cloned clone it if (!copies.ContainsKey(node)) { Node clone = new Node(node.val); copies[node] = clone; // Recursively clone neighbors foreach (Node neighbor in node.neighbors) { clone.neighbors.Add(CloneGraph(neighbor)); } } // Return the clone return copies[node]; } // Build graph public static Node BuildGraph() { Node node1 = new Node(0); Node node2 = new Node(1); Node node3 = new Node(2); Node node4 = new Node(3); node1.neighbors.Add(node2); node1.neighbors.Add(node3); node2.neighbors.Add(node1); node2.neighbors.Add(node3); node3.neighbors.Add(node1); node3.neighbors.Add(node2); node3.neighbors.Add(node4); node4.neighbors.Add(node3); return node1; } // Compare two graphs for structural and value equality public static bool CompareGraphs(Node node1 Node node2 Dictionary<Node Node> visited) { if (node1 == null || node2 == null) return node1 == node2; if (node1.val != node2.val || node1 == node2) return false; visited[node1] = node2; if (node1.neighbors.Count != node2.neighbors.Count) return false; for (int i = 0; i < node1.neighbors.Count; i++) { Node n1 = node1.neighbors[i]; Node n2 = node2.neighbors[i]; if (visited.ContainsKey(n1)) { if (visited[n1] != n2) return false; } else { if (!CompareGraphs(n1 n2 visited)) return false; } } return true; } // Driver Code public static void Main() { Node original = BuildGraph(); // Clone the graph using DFS Node cloned = CloneGraph(original); // Compare original and cloned graph bool isEqual = CompareGraphs(original cloned new Dictionary<Node Node>()); Console.WriteLine(isEqual ? 'true' : 'false'); } }
// Definition for a Node class Node { constructor(val = 0) { this.val = val; this.neighbors = []; } } // Map to hold original node to its copy const copies = new Map(); // Function to clone the graph using DFS function cloneGraph(node) { // If the node is NULL return NULL if (node === null) return null; // If node is not yet cloned clone it if (!copies.has(node)) { const clone = new Node(node.val); copies.set(node clone); // Recursively clone neighbors for (let neighbor of node.neighbors) { clone.neighbors.push(cloneGraph(neighbor)); } } // Return the clone return copies.get(node); } // Build graph function buildGraph() { const node1 = new Node(0); const node2 = new Node(1); const node3 = new Node(2); const node4 = new Node(3); node1.neighbors.push(node2 node3); node2.neighbors.push(node1 node3); node3.neighbors.push(node1 node2 node4); node4.neighbors.push(node3); return node1; } // Compare two graphs for structural and value equality function compareGraphs(node1 node2 visited = new Map()) { if (!node1 || !node2) return node1 === node2; if (node1.val !== node2.val || node1 === node2) return false; visited.set(node1 node2); if (node1.neighbors.length !== node2.neighbors.length) return false; for (let i = 0; i < node1.neighbors.length; i++) { const n1 = node1.neighbors[i]; const n2 = node2.neighbors[i]; if (visited.has(n1)) { if (visited.get(n1) !== n2) return false; } else { if (!compareGraphs(n1 n2 visited)) return false; } } return true; } // Driver Code const original = buildGraph(); // Clone the graph using DFS const cloned = cloneGraph(original); // Compare original and cloned graph console.log(compareGraphs(original cloned) ? 'true' : 'false');
Uitvoer
true


