Invoegsortering en selectiesortering zijn twee populaire sorteeralgoritmen, en hun belangrijkste verschil ligt in de manier waarop ze elementen selecteren en in een gesorteerde volgorde plaatsen.
Selectie Sorteren:
- Bij selectiesortering wordt de invoerarray in twee delen verdeeld: een gesorteerd deel en een ongesorteerd deel.
- Het algoritme vindt herhaaldelijk het minimumelement in het ongesorteerde deel en verwisselt dit met het meest linkse element van het ongesorteerde deel, waardoor het gesorteerde deel met één element wordt uitgebreid.
- Selectiesortering heeft in alle gevallen een tijdscomplexiteit van O(n^2).
Invoegsoort:
- Bij invoegsortering wordt de invoerarray ook in twee delen verdeeld: een gesorteerd deel en een ongesorteerd deel.
Het algoritme pakt een element uit het ongesorteerde deel en plaatst dit op de juiste positie in het gesorteerde deel, waarbij de grotere elementen één positie naar rechts worden verschoven.
Invoegsortering heeft in het slechtste geval een tijdscomplexiteit van O(n^2), maar kan beter presteren op gedeeltelijk gesorteerde arrays, met in het beste geval een tijdscomplexiteit van O(n).
Belangrijkste verschillen: - Selectiesortering scant het ongesorteerde deel om het minimale element te vinden, terwijl invoegsortering het gesorteerde deel scant om de juiste positie te vinden om het element te plaatsen.
Selectiesortering vereist minder swaps dan invoegsortering, maar meer vergelijkingen.
Invoegsortering is efficiënter dan selectiesortering wanneer de invoerarray gedeeltelijk of bijna gesorteerd is, terwijl selectiesortering beter presteert wanneer de array in hoge mate ongesorteerd is.
Samenvattend hebben beide algoritmen een vergelijkbare tijdscomplexiteit, maar hun selectie- en plaatsingsmethoden verschillen. De keuze hiertussen hangt af van de kenmerken van de invoergegevens en de specifieke vereisten van het betreffende probleem.
Voordelen van invoegsortering:
- Eenvoudig en gemakkelijk te begrijpen en te implementeren.
- Efficiënt voor kleine datasets of bijna gesorteerde gegevens.
- In-place sorteeralgoritme, wat betekent dat er geen extra geheugen nodig is.
- Stabiel sorteeralgoritme, wat betekent dat het de relatieve volgorde van gelijke elementen in de invoerarray behoudt.
Nadelen van invoegsortering:
- Inefficiënt voor grote datasets of omgekeerd geordende data, met in het slechtste geval een tijdscomplexiteit van O(n^2).
- Invoegsortering heeft veel swaps, waardoor het op moderne computers traag kan worden.
Voordelen van Selectie Sorteren:
- Eenvoudig en gemakkelijk te begrijpen en te implementeren.
- Efficiënt voor kleine datasets of bijna gesorteerde gegevens.
- In-place sorteeralgoritme, wat betekent dat er geen extra geheugen nodig is.
Nadelen van selectiesortering:
- Inefficiënt voor grote datasets, met in het slechtste geval een tijdscomplexiteit van O(n^2).
- Selectie sorteren heeft veel vergelijkingen, waardoor het op moderne computers traag kan zijn.
- Onstabiel sorteeralgoritme, wat betekent dat het mogelijk niet de relatieve volgorde van gelijke elementen in de invoerarray handhaaft.
In dit artikel bespreken we het verschil tussen de invoegsoort en de selectiesoort:
Invoegsoort is een eenvoudig sorteeralgoritme dat vergelijkbaar is met de manier waarop u speelkaarten in uw handen sorteert. De array is virtueel opgesplitst in een gesorteerd en een ongesorteerd deel. Waarden uit het ongesorteerde deel worden opgepakt en op de juiste positie in het gesorteerde deel geplaatst.
Algoritme:
Om een array met grootte n in oplopende volgorde te sorteren:
- Herhaal van arr[1] naar arr[n] over de array.
- Vergelijk het huidige element (sleutel) met zijn voorganger.
- Als het sleutelelement kleiner is dan zijn voorganger, vergelijk het dan met de voorgaande elementen. Verplaats de grotere elementen één positie naar boven om ruimte te maken voor het verwisselde element.
Hieronder ziet u de afbeelding om de invoegsortering te illustreren:
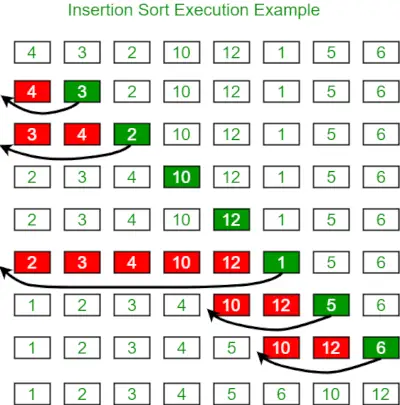
Hieronder vindt u het programma voor hetzelfde:
C++
// C++ program for the insertion sort> #include> using> namespace> std;> // Function to sort an array using> // insertion sort> void> insertionSort(>int> arr[],>int> n)> {> >int> i, key, j;> >for> (i = 1; i key = arr[i]; j = i - 1; // Move elements of arr[0..i-1], // that are greater than key to // one position ahead of their // current position while (j>= 0 && arr[j]> sleutel) { arr[j + 1] = arr[j]; j = j-1; } arr[j + 1] = sleutel; } } // Functie voor het afdrukken van een array van grootte N void printArray(int arr[], int n) { int i; // Druk de array af voor (i = 0; i cout<< arr[i] << ' '; } cout << endl; } // Driver Code int main() { int arr[] = { 12, 11, 13, 5, 6 }; int N = sizeof(arr) / sizeof(arr[0]); // Function Call insertionSort(arr, N); printArray(arr, N); return 0; }> |
>
>
Java
// Java program for the above approach> import> java.util.*;> class> GFG> {> > // Function to sort an array using> // insertion sort> static> void> insertionSort(>int> arr[],>int> n)> {> >int> i, key, j;> >for> (i =>1>; i { key = arr[i]; j = i - 1; // Move elements of arr[0..i-1], // that are greater than key to // one position ahead of their // current position while (j>= 0 && arr[j]> sleutel) { arr[j + 1] = arr[j]; j = j-1; } arr[j + 1] = sleutel; } } // Functie voor het afdrukken van een array van grootte N static void printArray(int arr[], int n) { int i; // Druk de array af voor (i = 0; i System.out.print(arr[i] + ' '); } System.out.println(); } // Stuurprogrammacode public static void main(String[ ] args) { int arr[] = { 12, 11, 13, 5, 6 }; // Functieaanroep insertionSort(arr, N); Deze code is bijgedragen door code_hunt> |
>
>
Python3
# Python 3 program for the insertion sort> # Function to sort an array using> # insertion sort> def> insertionSort(arr, n):> >i>=> 0> >key>=> 0> >j>=> 0> >for> i>in> range>(>1>,n,>1>):> >key>=> arr[i]> >j>=> i>-> 1> ># Move elements of arr[0..i-1],> ># that are greater than key to> ># one position ahead of their> ># current position> >while> (j>>=> 0> and> arr[j]>sleutel):> >arr[j>+> 1>]>=> arr[j]> >j>=> j>-> 1> >arr[j>+> 1>]>=> key> # Function to print an array of size N> def> printArray(arr, n):> >i>=> 0> ># Print the array> >for> i>in> range>(n):> >print>(arr[i],end>=> ' '>)> >print>(>'
'>,end>=> '')> # Driver Code> if> __name__>=>=> '__main__'>:> >arr>=> [>12>,>11>,>13>,>5>,>6>]> >N>=> len>(arr)> ># Function Call> >insertionSort(arr, N)> >printArray(arr, N)> > ># This code is contributed by bgangwar59.> |
>
>
C#
// C# program for the above approach> using> System;> class> GFG> {> >// Function to sort an array using> >// insertion sort> >static> void> insertionSort(>int>[] arr,>int> n)> >{> >int> i, key, j;> >for> (i = 1; i { key = arr[i]; j = i - 1; // Move elements of arr[0..i-1], // that are greater than key to // one position ahead of their // current position while (j>= 0 && arr[j]> sleutel) { arr[j + 1] = arr[j]; j = j-1; } arr[j + 1] = sleutel; } } // Functie voor het afdrukken van een array van grootte N static void printArray(int[] arr, int n) { int i; // Druk de array af voor (i = 0; i { Console.Write(arr[i] + ' '); } Console.WriteLine(); } // Stuurprogrammacode static public void Main() { int[] arr = new int[] { 12, 11, 13, 5, 6 }; int N = arr.Length; // Functieaanroep insertionSort(arr, N); bijgedragen door Dharanendra LV> |
>
>
Javascript
> // JavaScript program for the above approach> // Function to sort an array using> // insertion sort> function> insertionSort(arr,n)> {> >let i, key, j;> >for> (i = 1; i { key = arr[i]; j = i - 1; // Move elements of arr[0..i-1], // that are greater than key to // one position ahead of their // current position while (j>= 0 && arr[j]> sleutel) { arr[j + 1] = arr[j]; j = j-1; } arr[j + 1] = sleutel; } } // Functie voor het afdrukken van een array van grootte N function printArray(arr,n) { let i; // Druk de array af voor (i = 0; i document.write(arr[i] + ' '); } document.write(' '); } // Stuurprogrammacode let arr=[12, 11 , 13, 5, 6]; let N = arr.length; // Functieaanroep insertionSort(arr, N); printArray(arr, N); |
>5 6 11 12 13>
De selectie sorteren algoritme sorteert een array door herhaaldelijk het minimumelement (in oplopende volgorde) uit het ongesorteerde deel te vinden en dit aan het begin te plaatsen. Het algoritme onderhoudt twee subarrays in een gegeven array.
- De subarray is al gesorteerd.
- De resterende subarray is ongesorteerd.
Bij elke iteratie van de selectiesortering wordt het minimumelement (rekening houdend met de oplopende volgorde) uit de ongesorteerde subarray gekozen en naar de gesorteerde subarray verplaatst.
Hieronder ziet u een voorbeeld om de bovenstaande stappen uit te leggen:
arr[] = 64 25 12 22 11 // Find the minimum element in arr[0...4] // and place it at beginning 11 25 12 22 64 // Find the minimum element in arr[1...4] // and place it at beginning of arr[1...4] 11 12 25 22 64 // Find the minimum element in arr[2...4] // and place it at beginning of arr[2...4] 11 12 22 25 64 // Find the minimum element in arr[3...4] // and place it at beginning of arr[3...4] 11 12 22 25 64>
Hieronder vindt u het programma voor hetzelfde:
C++
// C++ program for implementation of> // selection sort> #include> using> namespace> std;> // Function to swap two number> void> swap(>int>* xp,>int>* yp)> {> >int> temp = *xp;> >*xp = *yp;> >*yp = temp;> }> // Function to implement the selection> // sort> void> selectionSort(>int> arr[],>int> n)> {> >int> i, j, min_idx;> >// One by one move boundary of> >// unsorted subarray> >for> (i = 0; i // Find the minimum element // in unsorted array min_idx = i; for (j = i + 1; j if (arr[j] min_idx = j; // Swap the found minimum element // with the first element swap(&arr[min_idx], &arr[i]); } } // Function to print an array void printArray(int arr[], int size) { int i; for (i = 0; i cout << arr[i] << ' '; } cout << endl; } // Driver Code int main() { int arr[] = { 64, 25, 12, 22, 11 }; int n = sizeof(arr) / sizeof(arr[0]); // Function Call selectionSort(arr, n); cout << 'Sorted array:
'; // Print the array printArray(arr, n); return 0; }> |
>
>
Java
// Java program for implementation of> // selection sort> import> java.util.*;> class> GFG> {> // Function to implement the selection> // sort> static> void> selectionSort(>int> arr[],>int> n)> {> >int> i, j, min_idx;> >// One by one move boundary of> >// unsorted subarray> >for> (i =>0>; i 1; i++) { // Find the minimum element // in unsorted array min_idx = i; for (j = i + 1; j if (arr[j] min_idx = j; // Swap the found minimum element // with the first element int temp = arr[min_idx]; arr[min_idx]= arr[i]; arr[i] = temp; } } // Function to print an array static void printArray(int arr[], int size) { int i; for (i = 0; i System.out.print(arr[i]+ ' '); } System.out.println(); } // Driver Code public static void main(String[] args) { int arr[] = { 64, 25, 12, 22, 11 }; int n = arr.length; // Function Call selectionSort(arr, n); System.out.print('Sorted array:
'); // Print the array printArray(arr, n); } } // This code is contributed by aashish1995> |
>
>
Python3
# Python3 program for implementation of> # selection sort> # Function to implement the selection> # sort> def> selectionSort(arr, n):> ># One by one move boundary of> ># unsorted subarray> >for> i>in> range>(n>-> 1>):> ># Find the minimum element> ># in unsorted array> >min_idx>=> i> >for> j>in> range>(i>+> 1>, n):> >if> (arr[j] min_idx = j # Swap the found minimum element # with the first element arr[min_idx], arr[i] = arr[i], arr[min_idx] # Function to print an array def printArray(arr, size): for i in range(size): print(arr[i], end = ' ') print() # Driver Code if __name__ == '__main__': arr = [64, 25, 12, 22, 11] n = len(arr) # Function Call selectionSort(arr, n) print('Sorted array: ') # Print the array printArray(arr, n) # This code is contributed by ukasp> |
>
>
C#
Python rstrip
// C# program for implementation of> // selection sort> using> System;> public> class> GFG> {> // Function to implement the selection> // sort> static> void> selectionSort(>int> []arr,>int> n)> {> >int> i, j, min_idx;> >// One by one move boundary of> >// unsorted subarray> >for> (i = 0; i { // Find the minimum element // in unsorted array min_idx = i; for (j = i + 1; j if (arr[j] min_idx = j; // Swap the found minimum element // with the first element int temp = arr[min_idx]; arr[min_idx]= arr[i]; arr[i] = temp; } } // Function to print an array static void printArray(int []arr, int size) { int i; for (i = 0; i Console.Write(arr[i]+ ' '); } Console.WriteLine(); } // Driver Code public static void Main(String[] args) { int []arr = { 64, 25, 12, 22, 11 }; int n = arr.Length; // Function Call selectionSort(arr, n); Console.Write('Sorted array:
'); // Print the array printArray(arr, n); } } // This code is contributed by gauravrajput1> |
>
>
Javascript
> // Javascript program for implementation of> // selection sort> // Function to implement the selection> // sort> function> selectionSort(arr, n)> {> >let i, j, min_idx;> > >// One by one move boundary of> >// unsorted subarray> >for>(i = 0; i { // Find the minimum element // in unsorted array min_idx = i; for(j = i + 1; j if (arr[j] min_idx = j; // Swap the found minimum element // with the first element let temp = arr[min_idx]; arr[min_idx]= arr[i]; arr[i] = temp; } } // Function to print an array function printArray(arr, size) { let i; for(i = 0; i { document.write(arr[i] + ' '); } document.write(' '); } // Driver Code let arr = [ 64, 25, 12, 22, 11 ]; let n = arr.length; // Function Call selectionSort(arr, n); document.write('Sorted array: '); // Print the array printArray(arr, n); // This code is contributed by rag2127> |
>
>Uitgang:
Sorted array: 11 12 22 25 64>
Tabelvormig verschil tussen invoegsortering en selectiesortering:
| Invoegsortering | Selectie Sorteren | |
|---|---|---|
| 1. | Voegt de waarde in de voorgesorteerde array in om de reeks waarden in de array te sorteren. | Zoekt het minimum/maximum aantal uit de lijst en sorteert dit in oplopende/aflopende volgorde. |
| 2. | Het is een stabiel sorteeralgoritme. | Het is een onstabiel sorteeralgoritme. |
| 3. | De tijdscomplexiteit in het beste geval is Ω(N) wanneer de array al in oplopende volgorde staat. Het heeft Θ(N2) in het slechtste en gemiddelde geval. | Voor het beste geval, het slechtste geval en de gemiddelde selectiesoort hebben de complexiteit Θ(N2). |
| 4. | Het aantal vergelijkingsbewerkingen dat in dit sorteeralgoritme wordt uitgevoerd, is minder dan het uitgevoerde omwisselen. | Het aantal vergelijkingsbewerkingen dat in dit sorteeralgoritme wordt uitgevoerd, is groter dan het aantal uitgevoerde verwisselingen. |
| 5. | Het is efficiënter dan de sortering Selectie. | Het is minder efficiënt dan de invoegsoort. |
| 6. | Hier is het element vooraf bekend en zoeken we naar de juiste positie om ze te plaatsen. | De locatie waar het element moet worden geplaatst is eerder bekend, we zoeken naar het element dat op die positie moet worden ingevoegd. |
| 7. | De invoegsoort wordt gebruikt wanneer:
| De selectiesortering wordt gebruikt wanneer
|
| 8. | De invoegsortering is adaptief, dat wil zeggen efficiënt voor datasets die al substantieel zijn gesorteerd: de tijdscomplexiteit is dat ook O(kn) wanneer elk element in de invoer niet meer is dan k plaatsen verwijderd van de gesorteerde positie | Selectiesortering is een intern sorteeralgoritme voor vergelijkingen |
