Algoritme is een stap-voor-stap procedure voor het oplossen van een probleem of het volbrengen van een taak. In de context van datastructuren en algoritmen is het een reeks goed gedefinieerde instructies voor het uitvoeren van een specifieke rekentaak. Algoritmen zijn van fundamenteel belang voor de informatica en spelen een zeer belangrijke rol bij het ontwerpen van efficiënte oplossingen voor verschillende problemen. Het begrijpen van algoritmen is essentieel voor iedereen die geïnteresseerd is in het beheersen van datastructuren en algoritmen.

Inhoudsopgave

img css uitlijnen

• Wat is een algoritme?
• Hoe werken algoritmen?
• Wat maakt een goed algoritme?
• Wat is de noodzaak van algoritmen?
• Voorbeelden van algoritmen
• Hoe schrijf je een algoritme?
• Leer de basisprincipes van algoritmen
• Analyse van algoritmen
• Soorten algoritmen

Wat is een algoritme?

Een algoritme is een eindige reeks goed gedefinieerde instructies die kunnen worden gebruikt om een ​​rekenprobleem op te lossen. Het biedt een stapsgewijze procedure die een invoer omzet in een gewenste uitvoer.

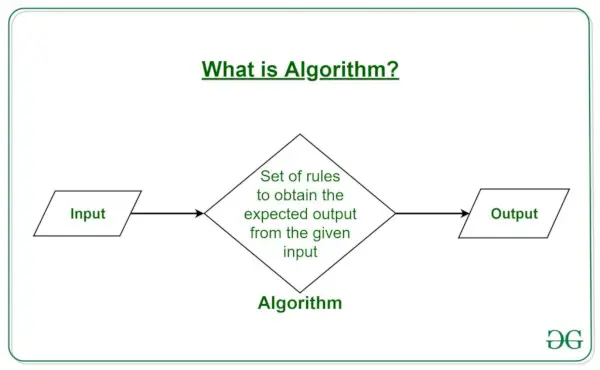
Hoe werken algoritmen?

Algoritmen volgen doorgaans een logische structuur:

• Invoer: Het algoritme ontvangt invoergegevens.
• Verwerken: Het algoritme voert een reeks bewerkingen uit op de invoergegevens.
• Uitgang: Het algoritme produceert de gewenste uitvoer.

Kenmerken van een algoritme:

• Duidelijk en eenduidig: Het algoritme moet ondubbelzinnig zijn. Elk van de stappen moet in alle aspecten duidelijk zijn en tot slechts één betekenis leiden.
• Goed gedefinieerde invoer: Als een algoritme zegt dat er invoer moet worden ingevoerd, moeten het goed gedefinieerde invoergegevens zijn. Het kan al dan niet input vereisen.
• Goed gedefinieerde uitgangen: Het algoritme moet duidelijk definiëren welke output zal worden opgeleverd en het moet ook goed gedefinieerd zijn. Het moet minimaal 1 output opleveren.
• Eindigheid: Het algoritme moet eindig zijn, dat wil zeggen dat het na een eindige tijd moet eindigen.
• Redelijk: Het algoritme moet eenvoudig, generiek en praktisch zijn, zodat het kan worden uitgevoerd met redelijke beperkingen en middelen.
• Taalonafhankelijk: Het algoritme moet taalonafhankelijk zijn, dat wil zeggen dat het eenvoudige instructies moeten zijn die in elke taal kunnen worden geïmplementeerd, en toch zal de output hetzelfde zijn als verwacht.

Wat is de noodzaak van algoritmen?

Algoritmen zijn essentieel voor het efficiënt en effectief oplossen van complexe computerproblemen. Ze bieden een systematische aanpak voor:

vba

• Problemen oplossen: Algoritmen splitsen problemen op in kleinere, beheersbare stappen.
• Oplossingen optimaliseren: Algoritmen vinden de beste of bijna optimale oplossingen voor problemen.
• Taken automatiseren: Algoritmen kunnen repetitieve of complexe taken automatiseren, waardoor tijd en moeite worden bespaard.

Voorbeelden van algoritmen

Hieronder staan ​​enkele voorbeelden van algoritmen:

verschil tussen vos en wolf

• Sorteeralgoritmen: Samenvoegen, snel sorteren, heap sorteren
• Zoekalgoritmen: Lineair zoeken, binair zoeken, hashen
• Grafiekalgoritmen: Het algoritme van Dijkstra, het algoritme van Prim, het algoritme van Floyd-Warshall
• Algoritmen voor het matchen van strings: Knuth-Morris-Pratt-algoritme, Boyer-Moore-algoritme

Hoe schrijf je een algoritme?

Volg deze stappen om een ​​algoritme te schrijven:

• Definieer het probleem: Geef duidelijk aan welk probleem moet worden opgelost.
• Ontwerp het algoritme: Kies een geschikt algoritmeontwerpparadigma en ontwikkel een stapsgewijze procedure.
• Implementeer het algoritme: Vertaal het algoritme naar een programmeertaal.
• Testen en debuggen: Voer het algoritme uit met verschillende invoer om de juistheid en efficiëntie ervan te garanderen.
• Analyseer het algoritme: Bepaal de tijd- en ruimtecomplexiteit ervan en vergelijk deze met alternatieve algoritmen.

Leer de basisprincipes van algoritmen

• Wat is algoritme | Inleiding tot algoritmen
• Definitie, typen, complexiteit, voorbeelden van algoritmen
• Algoritmen Ontwerptechnieken
• Waarom is analyse van een algoritme belangrijk?

Analyse van algoritmen

• Asymptotische analyse
• Slechtste, gemiddelde en beste gevallen
• Asymptotische notaties
• Onder- en bovengrenstheorie
• Inleiding tot geamortiseerde analyse
• Wat betekent ‘ruimtecomplexiteit’?
• Polynoom tijdbenaderingsschema
• Boekhoudmethode | Geamortiseerde analyse
• Potentiële methode in geamortiseerde analyse

Soorten algoritmen

Algoritmen kunnen van verschillende typen zijn, afhankelijk van wat ze doen en hoe ze zijn gemaakt. Enkele veel voorkomende typen zijn:

1. Algoritmen zoeken en sorteren

• Inleiding tot zoekalgoritmen
• Inleiding tot het sorteeralgoritme
• Stabiele en onstabiele sorteeralgoritmen
• Ondergrens voor op vergelijkingen gebaseerde sorteeralgoritmen
• Kan de runtimecomplexiteit van een op vergelijkingen gebaseerd sorteeralgoritme kleiner zijn dan N logN?
• Welk sorteeralgoritme maakt het minimale aantal geheugenschrijfbewerkingen?

2. Hebzuchtige algoritmen

• Inleiding tot hebzuchtige algoritmen
• Probleem met activiteitselectie
• Huffman-codering
• Probleem met taakvolgorde
• Quiz over hebzuchtige algoritmen
• Minimumaantal perrons vereist voor een trein-/busstation

3. Dynamische programmeeralgoritmen

• Inleiding tot dynamisch programmeren
• Overlappende deelproblemen Eigenschap
• Optimale onderbouweigenschap
• Langste stijgende vervolgreeks
• Langste gemeenschappelijke vervolgreeks
• Min. kostenpad
• Muntwissel
• Vermenigvuldiging van matrixketens
• 0-1 Knapzakprobleem
• Langste palindrome vervolgreeks
• Palindroompartitionering

4. Algoritmen voor het zoeken naar patronen

• Inleiding tot het zoeken naar patronen
• Naïef zoeken naar patronen
• KMP-algoritme
• Rabin-Karp-algoritme
• Patroon zoeken met behulp van een combinatie van alle achtervoegsels
• Aho-Corasick-algoritme voor het zoeken naar patronen
• Z-algoritme (algoritme voor het zoeken naar lineaire tijdpatronen)

5. Backtracking-algoritme

• Inleiding tot Backtracking
• Druk alle permutaties van een bepaalde string af
• Het tourprobleem van de ridder
• Rat in een doolhof
• N Koningin Probleem
• Subset som
• m Kleurprobleem
• Hamiltoniaanse cyclus
• Sudoku

6. Verdeel en heers-algoritme

• Inleiding tot Verdeel en Heers
• Sortering samenvoegen
• Schrijf je eigen pow(x, n) om x*n te berekenen
• Tel inversies
• Dichtstbijzijnde paar punten
• Strassen's matrixvermenigvuldiging

7. Geometrisch algoritme

• Inleiding tot geometrische algoritmen
• Dichtstbijzijnde paar punten | O(nlogn) Implementatie
• Hoe controleer ik of een bepaald punt binnen of buiten een veelhoek ligt?
• Hoe controleer ik of twee gegeven lijnsegmenten elkaar snijden?
• Gegeven n lijnsegmenten, zoek dan of twee segmenten elkaar snijden
• Hoe je kunt controleren of de gegeven vier punten een vierkant vormen
• Convexe romp met behulp van het algoritme van Jarvis of Wrapping

8. Wiskundige algoritmen

• Inleiding tot wiskundige algoritmen
• Schrijf een efficiënte methode om te controleren of een getal een veelvoud van 3 is
• Schrijf een programma om twee getallen op te tellen in grondtal 14
• Programma voor Fibonacci-getallen
• Gemiddelde van een stroom getallen
• Vermenigvuldig twee gehele getallen zonder gebruik te maken van vermenigvuldigings-, delings- en bitsgewijze operatoren, en zonder lussen
• Babylonische methode voor vierkantswortel
• Zeef van Eratosthenes
• De Driehoek van Pascal
• Zoek, gegeven een getal, het op één na kleinste palindroom
• Programma om twee polynomen op te tellen
• Vermenigvuldig twee veeltermen
• Tel achterliggende nullen in de faculteit van een getal

9. Bitsgewijze algoritmen

• Inleiding tot bitsgewijze algoritmen
• Kleine en grote Endian
• Detecteer tegenovergestelde tekens
• Wissel bits uit
• Schakel de meest rechtse ingestelde bit uit
• Bits roteren
• Volgende hoger nummer met hetzelfde aantal ingestelde bits
• Verwissel twee nibbles in een byte

10. Grafiekalgoritmen

• Inleiding tot gerandomiseerde algoritmen
• Lineariteit van verwachting
• Verwacht aantal pogingen tot succes
• Gerandomiseerde algoritmen | Set 0 (wiskundige achtergrond)
• Gerandomiseerde algoritmen | Set 1 (inleiding en analyse)
• Gerandomiseerde algoritmen | Set 2 (classificatie en toepassingen)
• Gerandomiseerde algoritmen | Set 3 (1/2 geschatte mediaan)
• Reservoirbemonstering