Nullen van een veelterm Als dit reële, denkbeeldige of complexe waarden zijn, wordt het resultaat nul (zoals de naam ook nul suggereert). Polynomen worden gebruikt om bepaalde fysieke verschijnselen te modelleren die in het echte leven voorkomen. Ze zijn erg handig bij het wiskundig beschrijven van situaties.

De nulpunten van een polynoom zijn alle x-waarden die de polynoom gelijk aan nul maken. Nullen van een polynoom vertellen ons over de x-intercepts van de grafiek van de polynoom. In dit artikel zullen we het hebben over de nulpunten van een polynoom, hoe je ze kunt vinden, de factorstelling, etc.

Inhoudsopgave

• Wat zijn nullen van veeltermen?
• Nullen van veeltermformule
• Hoe vind je de nul van een veelterm?
• Voor lineaire polynoom
• Voor kwadratisch polynoom
• Voor kubisch veelterm
• Factorstelling
• Relatie tussen nullen en coëfficiënt
• Relatie tussen nullen en coëfficiënt voor kwadratische vergelijking
• Relatie tussen nullen en coëfficiënt voor kubieke vergelijking
• Vergelijking vormen met nullen van polynoom
• Nullen in grafiek van veeltermen
• Fundamentele stelling van lineaire algebra
• Veelheid van een wortel
• Artikelen gerelateerd aan Nullen van Polynoom
• Voorbeeldproblemen op nullen van veeltermen
• Oefenproblemen op nullen van veeltermen

Wat zijn nullen van veeltermen?

Voor een polynoom P(x) zeggen we dat x = a het nulpunt van het polynoom is als P(a) = 0, en al deze nullen van een polynoom worden gewoonlijk nulpunten van een polynoom genoemd. Beschouw bijvoorbeeld f(x) = 3x – 12. Plaats nu x = 4 in de polynoom, d.w.z. f(4) = 3×4 – 12 = 0. Dus x = 4 is een nul van polynoom f( x) = 3x – 12.

Voorbeeld: Voor f(x) = x ³ – 6x ² + 11x – 6, is x = 1 nul?

Oplossing:

Om te controleren of x = 1 nul is van f(x) = x³– 6x²+ 11x – 6 of niet, zet x = 1 in (x)

f(1) = (1)³– 6×(1)²+ 11×(1) – 6

⇒ f(1) = 1 – 6 + 11 – 6 = 12 -12 = 0

Dus x = 1 is een nulpunt van f(x).

Nullen van veeltermformule

Voor een lineair polynoom met de vorm ax + b wordt het nulpunt gegeven door x = -b/a.

Voor een kwadratische polynoom van vorm ax²+ bx + c, de nul ervan wordt gegeven door x = {- b ± √D}/2a waarbij D Discriminant is, gegeven door b²– 4ac.

Hoe vind je de nul van een veelterm?

We kunnen de nulpunten van de polynoom voor verschillende soorten polynomen vinden met behulp van verschillende methoden die hieronder worden besproken.

• Voor lineaire polynoom
• Voor kwadratisch polynoom
• Voor kubisch veelterm

Voor lineaire polynoom

Voor lineaire veeltermen is het vinden van nul het gemakkelijkst. omdat er maar één nul is en die ook kan worden berekend door een eenvoudige herschikking van de polynoom na de gelijkstellende polynoom naar 0.

Zoek bijvoorbeeld nul voor lineaire polynoom f(x) = 2x – 7.

Oplossing:

Om nul van f(x) te vinden, stel je f(x) gelijk aan 0.

⇒ 2x – 7 = 0

⇒ 2x = 7

⇒ x = 7/2

tekenreeks naar gehele getallen

Voor kwadratisch polynoom

Er zijn verschillende methoden om wortels of nullen van een kwadratische polynoom te vinden, zoals het splitsen van de middelste term, een kwadratische formule die ook bekend staat als de Shree Dharacharya-formule, en het voltooien van het kwadraat dat enigszins lijkt op de kwadratische formule, aangezien de kwadratische formule komt vanaf het invullen van het kwadraat voor de algemene kwadratische vergelijking.

Leer meer over kwadratische vergelijkingen oplossen of polynomen en hoe deze op te lossen. De volgende voorbeelden tonen de methode voor het vinden van nulpunten van kwadratische veeltermen in detail.

Voorbeeld 1: Ontdek de nullen voor P(x) = x ² + 2x – 15.

Antwoord:

X²+ 2x – 15 = 0

⇒x²+ 5x – 3x – 15 = 0

⇒ x(x + 5) – 3(x + 5) = 0

⇒ (x – 3) (x + 5) = 0

⇒ x = 3, -5

Voorbeeld 2: Vind de nulpunten voor P(x) = x ² – 16x + 64.

Antwoord:

X²– 16x + 64 = 0

Vergelijkbaar met bijl²+ bx + c = 0,

we krijgen: a = 1, b = -16 en c = 64.

Dus,

⇒ x = 8, 8

Voor kubisch veelterm

Er zijn veel manieren om nullen van kubieke eenheden te vinden, zoals de rationele wortelstelling en staartdeling samen. Eén methode om wortels van een kubieke polynoom of een polynoom van een hogere graad te vinden, is als volgt:

Stap 1: Gebruik de rationele wortelstelling om de mogelijke wortels te vinden. dat wil zeggen: als een polynoom een ​​rationale wortel heeft, moet dit de deling van p/q zijn, waarbij p de gehele constante is en q de leidende coëfficiënt.

Stap 2: Nadat je één wortel hebt gevonden, deel je de polynoom met de factor gevormd door die wortel met behulp van staartdeling en schrijf je de polynoom als een product van quotiënt en deeltal.

Stap 3: Als het quotiënt een kwadratische uitdrukking is, los het dan op met de hierboven genoemde methoden voor kwadratische polynomen. Als het geen polynoom van graad 2 is, herhaal dan stap 1 en 2 totdat het quotiënt een polynoom van graad 2 wordt.

Stap 4: Het resultaat van stap 3 zijn de vereiste factoren, en door de factor gelijk te stellen aan 0 kunnen we de nulpunten van de polynoom vinden.

Voorbeeld: Zoek de nulpunten van de kubieke polynoom p(x) = x ³ + 2x ² – 5x – 6.

wat is 10 van de 100

Oplossing:

p(x) = x³+ 2x²– 5x – 6

Aangezien p/q = -6

Volgens de rationele wortelstelling zijn alle mogelijke rationale wortels van de polunominale delers van p/q.

Delers = ±1, ±2, ±3, ±6

x = -1, in p(x), krijgen we

p(-1) = (-1)³+ 2(-1)²– 5(-1) – 6

⇒ p(-1) = -1 + 2 + 5 – 6 = 0

Volgens de factorstelling is x + 1 dus de factor van p(x).

Dus x³+ 2x²– 5x – 6 = (x+1)(x²+x – 6)

⇒ x³+ 2x²– 5x – 6 = (x+1)(x-2)(x+3)

Voor nullen, p(x) = 0,

Nullen van p(x) zijn x = -1, x = 2 en x = -3.

Factorstelling

Voor de polynoom P(x) stelt de factorstelling dat als x =a nul is van P(X) iff x – a een factor is van P(x). dat wil zeggen dat beide volgende voorwaarden waar moeten zijn.

• Als a een nulpunt is van P(x), dan zal x−a een factor zijn van P(x)
• Als x−a een factor is van P(x), dan zal a een nul zijn van P(x)

Dit kan worden geverifieerd door naar eerdere voorbeelden te kijken. De factorstelling kan tot enkele interessante resultaten leiden, namelijk:

Resultaat 1: Als P(x) een polynoom is van graad n, en r een nulpunt is van P(x), dan kan P(x) in de volgende vorm worden geschreven:

P(x) = (x – r) Q(x)

Waarbij Q(x) een polynoom is van graad n-1 en kan worden bepaald door P(x) te delen door (x – r).

Resultaat 2: Als P(x) = (x-r)Q(x) en x = t een nulpunt is van Q(x), dan zal x = t ook een nulpunt zijn van P(x).

Om het bovenstaande feit te verifiëren,

Laten we zeggen dat t nul Q(x) is, wat betekent dat Q(t) = 0.

We weten dat r een nulpunt is van polynoom P(x), waarbij P(x) = (x – r) Q(x),

We moeten dus controleren of x = t ook een nul is van P(x), laten we x = t in P(x) plaatsen

⇒ P(t) = (t – r) Q(t) = 0

Dus x = t is ook een nulpunt P(x).

Bewezen dus.

Relatie tussen nullen en coëfficiënt

De relatie tussen de nullen en de coëfficiënt van de kwadratische en kubieke vergelijking wordt hieronder besproken.

Relatie tussen nullen en coëfficiënt voor kwadratische vergelijking

Voor een kwadratische vergelijking van de vorm ax²+ bx + c = 0, als de twee nulpunten van de kwadratische vergelijking α en β zijn, dan

• Som van wortel = α + β = -b/a
• Product van wortels = α × β = c/a

Relatie tussen nullen en coëfficiënt voor kubieke vergelijking

Als α, β en γ de wortel zijn van de kubieke polynoomas³+ bx²+ cx + d = 0, dan wordt de relatie tussen de nullen en coëfficiënten als volgt gegeven:

• a + b + c = -b/a
• α × β × γ= -d/a
• αβ + αγ + βγ = c/a

Vergelijking vormen met nullen van polynoom

• Voor een kwadratisch polynoom met nulpunten α en β wordt het kwadratisch polynoom gegeven door

X ² – (a + b)x + ab .

• Voor een kubieke polynoom met drie nullen α, β en γ, wordt de kubieke polynoom gegeven door

X ³ – (a + b + c)x ² + (ab + ag + bg)x – abg

Nullen in grafiek van veeltermen

In de grafiek van elk polynoom y = f(x) zijn reële nullen het punt waarvoor de grafiek de x-as snijdt of raakt. (aangezien een grafiek met een denkbeeldige nul nooit de x-as snijdt). Met andere woorden, als er drie reële oplossingen zijn voor een derdegraads polynoom, dan snijdt de grafiek van dat derdegraads polynoom de x-as drie keer, maar als er maar één reële oplossing is voor een derdegraads polynoom, dan snijdt de grafiek alleen de x-as. eenmaal.

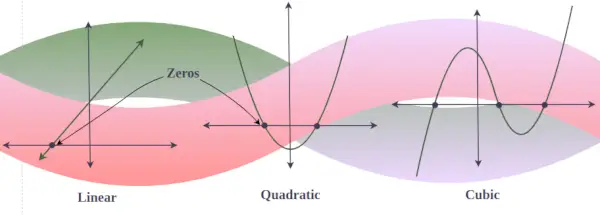
Fundamentele stelling van lineaire algebra

Als P(x) een polynoom van graad n is, dan zal P(x) precies n nullen hebben, waarvan sommige zich kunnen herhalen.

Linux-besturingssysteem

Dit betekent dat als we alle nullen opsommen en ze allemaal k keer opsommen, waarbij k de veelheid ervan is. We hebben precies n getallen in de lijst. Dit kan nuttig zijn omdat het ons een idee kan geven van het aantal nullen in een polynoom. We kunnen dus stoppen met zoeken naar nullen zodra we het vereiste aantal nullen hebben bereikt.

Veelheid van een wortel

Stel dat we een polynoom P(x) = 0 hebben die ontbindt in:

P(x) = (x – r) ^k (x – een) ^M

Als r een nul is van een polynoom en de exponent op zijn term die de wortel voortbracht k is, dan zeggen we dat r veelheid k . Nullen met een veelvoud van 1 worden vaak genoemd eenvoudig Nullen en nullen met een veelvoud van 2 worden dubbele wortels van de polynoom genoemd.

Voorbeeld: P(x) is een polynoom van graad 5, dat voor u is ontbonden. Noem de wortels en hun veelheid.

P(x) = 5x ⁵ −20x ⁴ +5x ³ +50x ² −20x−40=5(x+1) ² (x−2) ³

Oplossing:

Gegeven, P(x) = 5(x+1)²(x−2)³

⇒ P(x) = 5(x+1)(x+1)(x+1)(x−2)(x−2)

Om nullen te vinden, geldt P(x) = 0

⇒ x = -1, -1, 2, 2, 2

Merk op dat -1 twee keer voorkomt als nul, dus de veelheid ervan is 2, terwijl de veelheid van de nul 2 3 is.

Artikelen gerelateerd aan Nullen van Polynoom

• Polynoom
• Wortels van kwadratische vergelijking
• Algebraïsche expressie

Voorbeeldproblemen op nullen van veeltermen

Probleem 1: Gegeven dat x = 2 een nulpunt is van P(x) = x ³ +2x ² −5x−6. Zoek de andere twee nullen.

Oplossing:

Op basis van de fundamentele stelling die we eerder hebben bestudeerd, kunnen we zeggen dat P(x) 3 nullen zal hebben omdat het een polynoom van drie graden is. Eén ervan is x = 2.

We kunnen dus P(x) herschrijven,

P(x) = (x – 2) Q(x)

Om de andere twee nullen te vinden, moeten we de Q(x) vinden.

Q(x) kan worden bepaald door P(x) te delen door (x-2).

Na deling blijkt de Q(x) te zijn:

Q(x) = x²+ 4x + 3

Hieruit kunnen de resterende twee nullen worden afgeleid,

Q(x) = x²+ 3x + x + 3

⇒ x(x+3) + 1(x+3)

⇒ (x+1) (x+3)

Q(x) = 0,

x = -1, -3

De andere twee nullen zijn dus x = -1 en x = -3.

Probleem 2: Gegeven dat x = r een nulpunt van een polynoom is, zoek dan de andere nulpunten van het polynoom.

P(x) = x ³ -6x ² −16x; r = −2

Oplossing:

We weten dat x = -2 een nul is,

Dus P(x) kan worden herschreven als P(x) = (x + 2) Q(x) {Door het verdelingsalgoritme te gebruiken}

Om Q(x) te vinden, doen we hetzelfde als in de vorige vraag: we delen P(x) door (x + 2).

We krijgen,

Q(x) = x²– 8x

Om nu de andere twee nullen te vinden, factoriseert u Q(x)

Q(x) = x (x – 8) = 0

Java-klassediagram

De nullen zijn dus x = 0, 8.

We hebben dus drie nullen, x = -2, 0, 8.

Probleem 3: Vind de nulpunten van de polynoom, 4x ³ -3x ² -25x-6 = 0

Oplossing:

Truc om polynoomvergelijkingen met graad 3 op te lossen,

Zoek het kleinste gehele getal dat de polynomiale waarde 0 kan maken, begin met 1,-1,2, enzovoort...

we ontdekken dat we voor x = -2 de waarde van expressie nul krijgen.

Daarom is een van de wortels -2.

Volgens de factorstelling is a een van de nulpunten van de polynoom, dus (x-a) de factor van een gegeven polynoom.

Dus als volgt volgt: {x – (-2)} = (x+2) is een factor pof boven polynoom.

We krijgen een kwadratische vergelijking en er staat al een nul.

(4x²-11x-3)(x+2) = 0

Ontbind de kwadratische vergelijking in factoren,

(4x²-12x+x-3)(x+2) = 0

[4x(x-3)+1(x-3)](x+2) = 0

(4x+1)(x-3)(x+2) = 0

x = -2, x = 3, x = -1/4

Probleem 4: Vind de nulpunten van de polynoom, 4x ⁶ – 16x ⁴ = 0

Oplossing:

De polynoom heeft tot en met graad 6, dus er bestaan ​​6 nullen van de polynoom.

4x⁴(X²-4) = 0

4x⁴(X²-2²) = 0

4x⁴[(x+2)(x-2)] = 0

Daarom is x= 0, 0, 0, 0, 2, -2

lijstknooppunt in Java

Probleem 5: Vind de nulpunten van de polynoomfunctie f(x) = x ³ – 2x ² – 5x + 6

Oplossing:

Om de nulpunten van dit polynoom te vinden, stellen we f(x) = 0 in en lossen we x op:

f(x) = x³– 2x²– 5x + 6 = 0

Als d/a = 6

Volgens de rationele wortelstelling zijn alle mogelijke rationele wortels van de polunomiale:

Delers van d/a = ±1, ±2, ±3, ±6

x = 1, in p(x), krijgen we

f(1) = (1)³– 2(1)²– 5(1) – 6

f(-1) = 1 – 2 – 5 + 6 = 0

Dus volgens de factorstelling is x – 1 de factor van p(x).

Dus x³+ 2x²– 5x – 6 = (x-1)(x²-x – 6)

X³+ 2x²– 5x – 6 = (x-1)(x+2)(x-3)

Voor nullen, p(x) = 0,

Nullen van p(x) zijn x = 1, x = -2 en x = 3.

Oefenproblemen op nullen van veeltermen

1. Vind alle nulpunten van de polynoom f(x) = x ³ – 6x ² + 11x – 6

2. Bepaal alle nulpunten van de polynoom g(x) = 2x ⁴ – 7x ³ + 3x ² + 4x – 4

3. Zoek de nulpunten van de polynoom h(x) = x ⁵ – 3x ⁴ + 2x ³ – 6x ² +x+2

4. Bepaal alle nulpunten van de polynoom p(x) = 3x ⁴ – 16x ³ + 18x ² + 16x – 12.

Veelgestelde vragen over nullen van veeltermen

Wat zijn nullen van een veelterm?

Deze reële waarden, want de waarde van polynoom wordt 0, d.w.z. als p(x) een polynoom is, en p(a) = 0, dan is x = a de nul van p(x).

Hoe vind je de nullen van een veelterm?

Er zijn verschillende methoden voor verschillende polynomen om nullen te vinden, zoals voor het kwadratisch overlopen van de middelste term en de kwadratische formule. Voor lineaire, eenvoudige herschikking van variabelen en voor kubieke gebruiken we een combinatie van rationele wortelstelling, staartdeling, factorstelling en reststelling.

Kan een polynoom meer dan één nul hebben?

Ja, een polynoom kan meer dan één nul hebben. Sterker nog, de polynoom van n graden kan maximaal n reële nulpunten hebben.

Wat is de multipliciteit van een nul van een polynoom?

Bij het factorisatieproces komt er één factor of één nul van een polynoom en vervolgens een aantal keren een factor of een nul, dat heet de multipliciteit van die wortel.

Wat is de fundamentele stelling van algebra?

De fundamentele stelling van de algebra luidt: Als P(x) een polynoom van graad n is, dan zal P(x) precies n nullen hebben, waarvan sommige zich kunnen herhalen.

Heeft een polynoom met graad n altijd n reële wortels?

Nee, een polynoom met graad n heeft niet altijd n echte wortels, aangezien sommige wortels denkbeeldige of complexe getallen kunnen zijn.

Wat is de graad van nulpolynoom?

De graad van nulpolynoom is nul.