Z-SCORE IN STATISTIEKEN - DATA-WETENSCHAP

Z-score in statistieken is een meting van hoeveel standaarddeviaties een gegevenspunt verwijderd is van het gemiddelde van een verdeling. Laten we de z-score in de statistieken vinden. Een z-score van 0 geeft aan dat de score van het datapunt hetzelfde is als de gemiddelde score. Een positieve z-score geeft aan dat het datapunt boven het gemiddelde ligt, terwijl een negatieve z-score aangeeft dat het datapunt onder het gemiddelde ligt.

De formule voor het berekenen van een z-score is: z = (x – μ)/ p

Waar:

X: is de testwaarde
M: is het gemiddelde
bij: is de standaardwaarde

In dit artikel gaan we de volgende concepten bespreken:

Inhoudsopgave

Wat is Z-Score?
Hoe de Z-score berekenen?
Kenmerken van Z-Score
Bereken uitschieters met behulp van de Z-Score-waarde
Implementatie van Z-Score in Python
Toepassing van Z-Score
Z-scores versus standaarddeviatie
Waarom worden Z-scores standaardscores genoemd?

Wat is Z-Score?

De Z-score, ook wel de standaardscore genoemd, vertelt ons de afwijking van een gegevenspunt van het gemiddelde door dit uit te drukken in termen van standaardafwijkingen boven of onder het gemiddelde. Het geeft ons een idee van hoe ver een datapunt van het gemiddelde verwijderd is. Daarom wordt de Z-score gemeten in termen van standaardafwijking van het gemiddelde. Een Z-score van 2 geeft bijvoorbeeld aan dat de waarde 2 standaarddeviaties verwijderd is van het gemiddelde. Om een z-score te gebruiken, moeten we het populatiegemiddelde (μ) en ook de populatiestandaarddeviatie (σ) kennen.

De formule voor Z-Score

Een z-score kan worden berekend met behulp van de volgende formule.

z = (X – μ) / p

waar,

z = Z-score
X = Waarde van element
μ = Populatiegemiddelde
σ = Populatiestandaardafwijking

Hoe de Z-score berekenen?

We krijgen het populatiegemiddelde (μ), de standaarddeviatie van de populatie (σ) en de waargenomen waarde (x) in de probleemstelling. Als we deze vervangen in de Z-score-vergelijking, krijgen we de Z-Score-waarde. Afhankelijk van of de gegeven Z-Score positief of negatief is, kunnen we gebruiken positieve Z-tabel of negatieve Z-tabel beschikbaar online of op de achterkant van uw statistiekboek in de bijlage.

Voorbeeld 1:

U doet het GATE-examen en scoort 500. De gemiddelde score voor het GATE is 390 en de standaarddeviatie is 45. Hoe goed scoorde u op de toets vergeleken met de gemiddelde testpersoon?

Oplossing:

De volgende gegevens zijn direct beschikbaar in de bovenstaande vraagstelling

Ruwe score/waargenomen waarde = X = 500

Gemiddelde score = μ = 390

Standaardafwijking = σ = 45

Door de formule van z-score toe te passen,

z = (X – μ) / p

z = (500 – 390) / 45

z = 110 / 45 = 2,44

Dit betekent dat uw z-score is 2.44 .

Omdat de Z-Score positief 2,44 is, zullen we gebruik maken van de positieve Z-Tabel.

Laten we nu eens kijken Z-tabel (CC-BY) om te weten hoe goed u scoorde in vergelijking met de andere testpersonen.

Volg de onderstaande instructie om de waarschijnlijkheid uit de tabel te vinden.

np nullen

Hier, z-score = 2,44, welke i geeft aan dat het datapunt 2,44 standaardafwijkingen boven het gemiddelde ligt.

Breng eerst de eerste twee cijfers 2.4 in kaart op de Y-as.
Breng vervolgens langs de X-as 0,04 in kaart
Verbind beide assen. Het snijpunt van de twee geeft u de cumulatieve waarschijnlijkheid die hoort bij de Z-score-waarde waarnaar u op zoek bent

[Deze waarschijnlijkheid vertegenwoordigt het gebied onder de standaardnormale curve links van de Z-score]

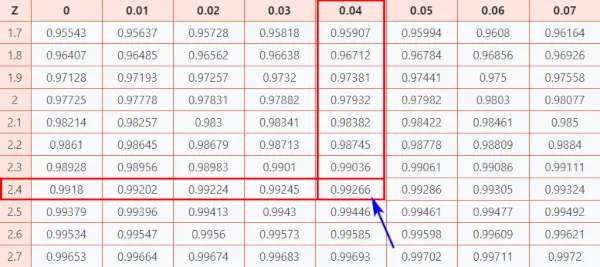
Normale verdelingstabel

Het resultaat is dat u de uiteindelijke waarde krijgt 0,99266 .

Nu moeten we vergelijken hoe onze oorspronkelijke score van 500 op het GATE-onderzoek zich verhoudt tot de gemiddelde score van de batch. Om dat te doen moeten we de cumulatieve waarschijnlijkheid die aan de Z-score is gekoppeld, omzetten in een procentuele waarde.

0,99266 × 100 = 99,266%

Tenslotte kun je zeggen dat je meer dan bijna goed hebt gepresteerd 99% van andere testpersonen.

Voorbeeld 2 : Wat is de kans dat een leerling tussen 350 en 400 scoort (met een gemiddelde score μ van 390 en een standaarddeviatie σ van 45)?

Oplossing:

Min.score = X₁= 350

Maximale score = X₂= 400

Door de formule van z-score toe te passen,

Met₁= (X1 – m) / p

Met₁= (350 – 390) / 45

Met₁= -40 / 45 = -0,88

Met₂= (X₂– m) / p

z2 = (400 – 390) / 45

Met₂= 10 / 45 = 0,22

Omdat z1 negatief is, zullen we naar een negatief moeten kijken Z-tabel en ontdek dat de cumulatieve waarschijnlijkheid p1, de eerste waarschijnlijkheid, gelijk is 0,18943 .

Met₂is positief, dus gebruiken we een positieve Z-tabel die een cumulatieve waarschijnlijkheid p oplevert₂van 0,58706 .

De uiteindelijke waarschijnlijkheid wordt berekend door p1 af te trekken van p₂:

p = p₂- P₁

p = 0,58706 – 0,18943 = 0,39763

De kans dat een leerling tussen de 350 en 400 scoort is 39,763% (0,39763 * 100).

Kenmerken van Z-Score

De omvang van de Z-score weerspiegelt hoe ver een gegevenspunt van het gemiddelde ligt in termen van standaarddeviaties.
Een element met een z-score van minder dan 0 betekent dat het element kleiner is dan het gemiddelde.
Z-scores maken de vergelijking van gegevenspunten uit verschillende distributies mogelijk.
Een element met een z-score groter dan 0 betekent dat het element groter is dan het gemiddelde.
Een element met een z-score gelijk aan 0 geeft aan dat het element gelijk is aan het gemiddelde.
Een element met een z-score gelijk aan 1 geeft aan dat het element 1 standaarddeviatie groter is dan het gemiddelde; een z-score gelijk aan 2, 2 standaarddeviaties groter dan het gemiddelde, enzovoort.
Een element met een z-score gelijk aan -1 geeft aan dat het element 1 standaarddeviatie minder is dan het gemiddelde; een z-score gelijk aan -2, 2 standaarddeviaties minder dan het gemiddelde, enzovoort.
Als het aantal elementen in een bepaalde set groot is, heeft ongeveer 68% van de elementen een z-score tussen -1 en 1; ongeveer 95% heeft een z-score tussen -2 en 2; ongeveer 99% heeft een z-score tussen -3 en 3. Dit staat bekend als de empirische regel en geeft het percentage gegevens weer binnen bepaalde standaardafwijkingen van het gemiddelde in een normale verdeling, zoals weergegeven in de onderstaande afbeelding

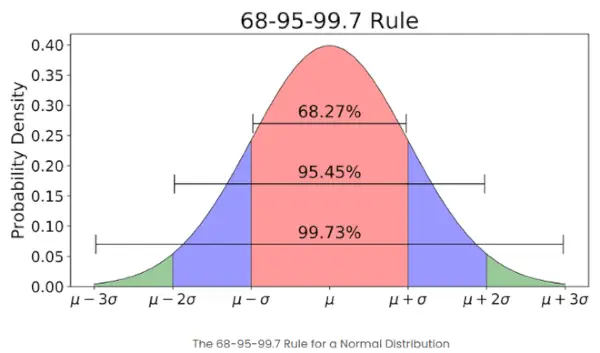
De empirische regel in normale verdeling

Bereken uitschieters met behulp van de Z-Score-waarde

We kunnen uitbijters in de gegevens berekenen met behulp van de z-scorewaarde van de gegevenspunten. De stappen om een uitbijtergegevenspunt te overwegen zijn als volgt:

Eerst verzamelen we de dataset waarin we de uitbijters willen zien
We berekenen het gemiddelde en de standaardafwijking van de dataset. Deze waarden worden gebruikt om de z-scorewaarde van elk datapunt te berekenen.
We berekenen de z-scorewaarde voor elk gegevenspunt. De formule voor het berekenen van de z-score-waarde is dezelfde als
Z = frac{{X – mu}}{{sigma}}
waarbij X het datapunt is, μ het gemiddelde van de gegevens en σ de standaardafwijking van de dataset.
We zullen de grenswaarde voor de z-score bepalen, waarna het datapunt als een uitbijter kan worden beschouwd. Deze grenswaarde is een hyperparameter die we bepalen afhankelijk van ons project.
Een datapunt waarvan de z-score groter is dan 3 betekent dat het datapunt niet tot het 99,73%-punt van de dataset behoort.
Elk datapunt waarvan de z-score groter is dan onze vastgestelde grenswaarde, wordt als een uitbijter beschouwd.

Rekening: Z-score voor detectie van uitschieters

Implementatie van Z-Score in Python

We kunnen Python gebruiken om de z-score-waarde van datapunten in de dataset te berekenen. We zullen ook de numpy-bibliotheek gebruiken om de gemiddelde en standaardafwijking van de dataset te berekenen.

Python3

 import numpy as np def calculate_z_score(data): # Mean of the dataset mean = np.mean(data) # Standard Deviation of tha dataset std_dev = np.std(data) # Z-score of tha data points z_scores = (data - mean) / std_dev return z_scores # Example dataset dataset = [3,9, 23, 43,53, 4, 5,30, 35, 50, 70, 150, 6, 7, 8, 9, 10] z_scores = calculate_z_score(dataset) print('Z-Score :',z_scores) # Data points which lies outside 3 standard deviatioms are outliers # i.e outside range of99.73% values outliers = [data_point for data_point,  z_score in zip(dataset, z_scores) if z_score>3] print(f'
De uitbijters in de dataset zijn {uitbijters}')>

Uitgang:

Z-score: [-0,7574907 -0,59097335 -0,20243286 0,35262498 0,6301539 -0,72973781
-0,70198492 -0,00816262 0,13060185 0,54689523 1,10195307 3,32218443
-0,67423202 -0,64647913 -0,61872624 -0,59097335 -0,56322046]
De uitschieters in de dataset zijn [150]

Toepassing van Z-Score

Z-scores worden vaak gebruikt voor het schalen van functies om verschillende functies op een gemeenschappelijke schaal te brengen. Het normaliseren van kenmerken zorgt ervoor dat ze geen gemiddelde en eenheidsvariantie hebben, wat gunstig kan zijn voor bepaalde machine learning-algoritmen, vooral die welke afhankelijk zijn van afstandsmetingen.
Z-scores kunnen worden gebruikt om uitbijters in een dataset te identificeren. Gegevenspunten met Z-scores boven een bepaalde drempel (meestal 3 standaardafwijkingen van het gemiddelde) kunnen als uitschieters worden beschouwd.
Z-scores kunnen worden gebruikt in algoritmen voor het detecteren van afwijkingen om gevallen te identificeren die aanzienlijk afwijken van het verwachte gedrag.
Z-scores kunnen worden toegepast om scheve verdelingen om te zetten in meer normale verdelingen.
Bij het werken met regressiemodellen kunnen Z-scores van residuen worden geanalyseerd om te controleren op homoscedasticiteit (constante variantie van residuen).
Z-scores kunnen worden gebruikt bij het schalen van functies door te kijken naar hun standaardafwijkingen van het gemiddelde.

Z-scores versus standaarddeviatie

Z-score	Standaardafwijking
Transformeer onbewerkte gegevens naar een gestandaardiseerde schaal.	Meet de hoeveelheid variatie of spreiding in een reeks waarden.
Maakt het gemakkelijker om waarden uit verschillende datasets te vergelijken, omdat ze de oorspronkelijke meeteenheden wegnemen.	Standaardafwijking behoudt de oorspronkelijke meeteenheden, waardoor deze minder geschikt is voor directe vergelijkingen tussen datasets met verschillende eenheden.
Geef aan hoe ver een datapunt van het gemiddelde verwijderd is in termen van standaarddeviaties, en geef daarmee een maatstaf voor de relatieve positie van het datapunt binnen de verdeling	Uitgedrukt in dezelfde eenheden als de oorspronkelijke gegevens, wat een absolute maatstaf geeft van hoe verspreid de waarden rond het gemiddelde liggen

Rekening: Z-scoretabel

Waarom worden Z-scores standaardscores genoemd?

Z-scores worden ook wel standaardscores genoemd omdat ze de waarde van een willekeurige variabele standaardiseren. Dit betekent dat de lijst met gestandaardiseerde scores een gemiddelde van 0 en een standaarddeviatie van 1,0 heeft. Z-scores maken het ook mogelijk scores op verschillende soorten variabelen te vergelijken. Dit komt omdat ze relatieve status gebruiken om scores van verschillende variabelen of verdelingen gelijk te stellen.

statische functie in Java

Z-scores worden vaak gebruikt om een variabele te vergelijken met een standaardnormale verdeling (met μ = 0 en σ = 1).

Z-Score in Statistieken – Veelgestelde vragen

Wat is de betekenis van positieve en negatieve Z-Scores?

Positieve Z-scores geven waarden aan die boven het gemiddelde liggen, terwijl negatieve Z-scores waarden onder het gemiddelde aangeven. Het teken geeft de richting van afwijking van het gemiddelde weer.

Wat betekent een Z-Score van 0?

Een Z-Score van 0 geeft aan dat de waarde van het datapunt precies op het gemiddelde van de dataset ligt. Het suggereert dat het datapunt noch boven, noch onder het gemiddelde ligt.

Wat is de 68-95-99.7-regel met betrekking tot Z-Scores?

De 68-95-99.7-regel, ook bekend als de empirische regel, stelt dat:

Ongeveer 68% van de gegevens valt binnen 1 standaardafwijking van het gemiddelde.
Ongeveer 95% valt binnen 2 standaarddeviaties.
Ongeveer 99,7% valt binnen 3 standaarddeviaties.

Kunnen Z-Scores worden gebruikt voor niet-normale verdelingen?

Z-Scores zijn gebaseerd op de aanname dat de gegevens een normale verdeling volgen. In de praktijk zijn Z-Scores echter gunstig voor gegevens die een normale verdeling volgen. Hoewel Z-Scores voor elke verdeling kunnen worden berekend, wordt hun interpretatie minder betrouwbaar en eenvoudig als het gaat om niet-normaal verdeelde gegevens.

Hoe kunnen Z-Scores worden toegepast in praktijksituaties?

Z-Scores hebben verschillende toepassingen, zoals in de financiële wereld voor portfolioanalyse, onderwijs voor gestandaardiseerde tests, gezondheid voor klinische beoordelingen en meer. Ze bieden een gestandaardiseerde maatstaf voor het vergelijken en interpreteren van gegevens.