De voorwaarde Memoriseren komt van het Latijnse woord memorandum ( onthouden ), wat in het Amerikaans-Engels gewoonlijk wordt afgekort tot memo, en wat betekent dat de resultaten van een functie worden omgezet in iets om te onthouden.
Bij computergebruik wordt memoisatie gebruikt om computerprogramma's te versnellen door de herhaalde berekening van resultaten te elimineren en door herhaalde oproepen naar functies te vermijden die dezelfde invoer verwerken.

Wat is memoriseren
Inhoudsopgave
- Wat is Memoiseren?
- Waarom wordt Memoisatie gebruikt>
- Waar kan Memoisatie worden gebruikt?
- Soorten memoriseren
- Hoe memorisatietechniek gebruikt bij dynamisch programmeren?
- Hoe verschilt Memoiseren van Tabelleren?
- Oefenproblemen coderen voor het onthouden
- Veelgestelde vragen
- 1) Is memoriseren beter dan DP?
- 2) Is memoiseren hetzelfde als caching?
- 3) Waarom gebeurt het memoiseren van bovenaf?
- 4) Maakt memoisatie gebruik van recursie?
- 5) Moet ik tabelleren of memoiseren gebruiken?
- 6) Waar wordt memoisatie gebruikt?
- 7) Waarom wordt het memoriseren genoemd?
- 8) Hoe vermindert het memoiseren de tijdcomplexiteit?
- 9) Wat is het verschil tussen memoiseren en caching?
- 10) Waarom is tabelleren sneller dan memoriseren?
- Conclusie
Waarom wordt Memoisatie gebruikt?
Memoiseren is een specifieke vorm van cachen waarin gebruikt wordt dynamisch programmeren . Het doel van caching is om de prestaties van onze programma's te verbeteren en gegevens toegankelijk te houden die later kunnen worden gebruikt. Het slaat feitelijk het eerder berekende resultaat van het subprobleem op en gebruikt het opgeslagen resultaat voor hetzelfde subprobleem. Dit neemt de extra moeite weg om steeds opnieuw voor hetzelfde probleem te berekenen. En we weten al dat als hetzelfde probleem zich keer op keer voordoet, dat probleem recursief van aard is.
Waar kan Memoisatie worden gebruikt?
We kunnen de memoisatietechniek gebruiken waarbij de gebruik van de eerder berekende resultaten komt in beeld. Dit soort problemen wordt meestal gebruikt in de context van herhaling , vooral als het om problemen gaat overlappende deelproblemen .
Laten we een voorbeeld nemen waarbij hetzelfde subprobleem zich keer op keer herhaalt.
Voorbeeld om te laten zien waar u memoisatie kunt gebruiken:
Let us try to find the factorial of a number .>
Hieronder staat een recursieve methode voor het vinden van de faculteit van een getal:
int faculteit(niet-ondertekend int n)
{
als (n == 0)
retour 1;
return n * faculteit(n – 1);
}
Wat gebeurt er als we deze recursieve methode gebruiken?
Als u de volledige code voor het bovenstaande fragment schrijft, zult u merken dat er 2 methoden in de code voorkomen:
1. factorial(n) 2. main()>
Als we nu meerdere zoekopdrachten hebben om de faculteit te vinden, zoals het vinden van de faculteit van 2, 3, 9 en 5, dan moeten we de methode factorial() vier keer aanroepen:
factorial(2) factorial(3) factorial(9) factorial(5)>
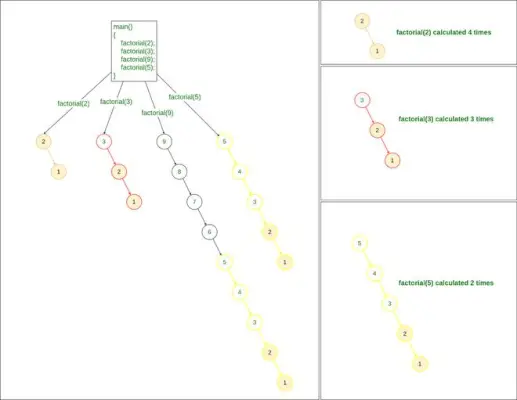
Recursieve methode om faculteit te vinden
Het is dus veilig om te zeggen dat voor het vinden van faculteiten van getallen K-getallen de benodigde tijdcomplexiteit gelijk zal zijn O(N*K)
- OP) om de faculteit van een bepaald getal te vinden, en
- PIJL) om de factorial() methode K verschillende keren aan te roepen.
Hoe kan memoriseren helpen bij dergelijke problemen?
Als we in het bovenstaande probleem opmerken, terwijl de berekeningsfaculteit van 9:
Java-methoden
- We berekenen de faculteit van 2
- We berekenen ook de faculteit van 3,
- en we berekenen ook de faculteit van 5
Als we dus het resultaat van elke afzonderlijke faculteit bij de eerste berekening opslaan, kunnen we de faculteit van elk vereist getal gemakkelijk in slechts O(1) tijd retourneren. Dit proces staat bekend als Memoriseren .
Oplossing met behulp van Memoization (Hoe werkt Memoization?):
Als we eerst de faculteit van 9 vinden en de resultaten van individuele deelproblemen opslaan, kunnen we gemakkelijk de faculteit van elke invoer in O(1) afdrukken.
Daarom zal de tijdcomplexiteit om faculteitsgetallen te vinden met behulp van memoisatie zijn OP)
- OP) om de faculteit van de grootste invoer te vinden
- O(1) om de faculteit van elke invoer af te drukken.
Soorten memoriseren
De implementatie van memoisatie hangt af van de veranderende parameters die verantwoordelijk zijn voor het oplossen van het probleem. Er zijn verschillende dimensies van caching die worden gebruikt bij de memoisatietechniek. Hieronder staan er enkele:
- 1D-memorisatie: De recursieve functie die slechts één argument heeft waarvan de waarde niet constant was na elke functieaanroep.
- 2D-memorisatie: De recursieve functie die slechts twee argumenten heeft waarvan de waarde niet constant was na elke functieaanroep.
- 3D-memorisatie : De recursieve functie die slechts drie argumenten heeft waarvan de waarden niet constant waren na elke functieaanroep.
Hoe wordt de Memoisatie-techniek gebruikt bij dynamisch programmeren?
Dynamisch programmeren helpt bij het efficiënt oplossen van problemen met overlappende deelproblemen en optimale eigenschappen van de onderbouw. Het idee achter dynamisch programmeren is om het probleem op te delen in kleinere deelproblemen en het resultaat op te slaan voor toekomstig gebruik, waardoor het niet meer nodig is om het resultaat herhaaldelijk te berekenen.
Er zijn twee benaderingen om een dynamische programmeeroplossing te formuleren:
- Top-down benadering: Deze aanpak volgt de memoriseren techniek . Het bestaat uit herhaling En cachen . Bij berekeningen vertegenwoordigt recursie het proces waarbij functies herhaaldelijk worden aangeroepen, terwijl cache verwijst naar het proces waarbij tussenresultaten worden opgeslagen.
- Bottom-up-benadering: Deze aanpak maakt gebruik van de tabel techniek om de dynamische programmeeroplossing te implementeren. Het behandelt dezelfde problemen als voorheen, maar zonder recursie. In deze benadering vervangt iteratie recursie. Er is dus geen sprake van een stack-overflow-fout of overhead van recursieve procedures.
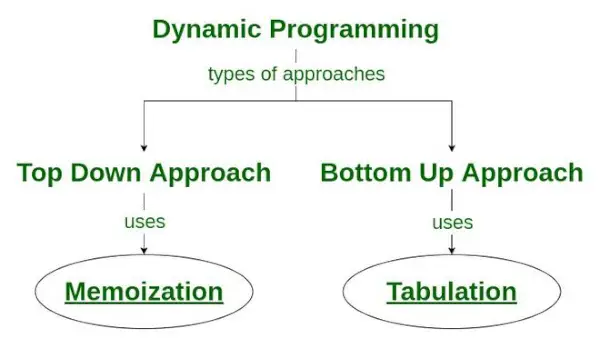
Hoe de Memoisatie-techniek wordt gebruikt bij dynamisch programmeren
Hoe verschilt Memoiseren van Tabelleren?

Tabelleren versus memoriseren
Voor meer details verwijzen wij u naar: Tabelleren versus memoriseren
Oefenproblemen bij het coderen bij het onthouden
| Vraag | Artikel | Oefening | Video |
|---|---|---|---|
| Tel manieren om de zoveelste trap te bereiken | Weergave | Oplossen | Horloge |
| Woordafbraakprobleem | DP-32 | Weergave | Oplossen | Horloge |
| Programma voor Fibonacci-getallen | Weergave | Oplossen | Horloge |
| nde Catalaans nummer | Weergave | Oplossen | Horloge |
| Goudmijnprobleem | Weergave | Oplossen | Horloge |
| Subsetsomprobleem | Weergave | Oplossen | Horloge |
| Een staaf snijden | Weergave | Oplossen | Horloge |
| Min. kostenpad | Weergave | Oplossen | Horloge |
| Minimum aantal sprongen om het einde te bereiken | Weergave | Oplossen | Horloge |
| Langste palindroomsubtekenreeks | Set 1 | Weergave | Oplossen | Horloge |
| Langste herhalende vervolgreeks | Weergave | Oplossen | Horloge |
| Tel manieren om de zoveelste trap te bereiken met behulp van stap 1, 2 of 3 | Weergave | Oplossen | Horloge |
| Aantal verschillende manieren om N uit te drukken als de som van 1, 3 en 4 | Weergave | Oplossen | Horloge |
| Tel het aantal manieren om een afstand af te leggen | Weergave | Oplossen | Horloge |
| Aantal arrays met opeenvolgend element met verschillende waarden | Weergave | Oplossen | Horloge |
| Grootste som aaneengesloten subarray | Weergave | Oplossen | Horloge |
| Kleinste som aaneengesloten subarray | Weergave | Oplossen | Horloge |
| Unieke paden in een raster met obstakels | Weergave | Oplossen | Horloge |
| Verschillende manieren om n op te tellen met getallen groter dan of gelijk aan m | Weergave | Oplossen | Horloge |
Veelgestelde vragen (FAQ's) over Memoiseren
1: Is memoiseren beter dan DP?
Memoiseren is de top-downbenadering voor het oplossen van een probleem met dynamisch programmeren. Het heet memoiseren omdat we een memo maken voor de waarden die het resultaat zijn van het oplossen van elk probleem.
2: Is memoiseren hetzelfde als caching?
Memoriseren is eigenlijk een specifiek type caching. De term caching kan over het algemeen verwijzen naar elke opslagtechniek (zoals HTTP-caching) voor toekomstig gebruik, maar memoiseren verwijst meer specifiek naar de caching-functie die de waarde retourneert.
3: Waarom gebeurt het memoiseren van bovenaf?
De top-downbenadering verdeelt het grote probleem in meerdere deelproblemen. als het deelprobleem al is opgelost, hergebruik dan het antwoord. Los anders het subprobleem op en sla het resultaat op in een geheugen.
4: Maakt memoisatie gebruik van recursie?
Memoriseren volgt een top-downbenadering om het probleem op te lossen. Het bestaat uit recursie en caching. Bij berekeningen vertegenwoordigt recursie het proces waarbij functies herhaaldelijk worden aangeroepen, terwijl cache verwijst naar het proces waarbij tussenresultaten worden opgeslagen.
5: Moet ik tabelleren of memoiseren gebruiken?
Voor problemen waarbij alle subproblemen moeten worden opgelost, presteert tabelleren doorgaans beter dan memoiseren met een constante factor. Dit komt omdat de tabel geen overhead van recursie heeft, waardoor de tijd voor het oplossen van de recursie-oproepstapel uit het stapelgeheugen wordt verkort.
Wanneer een deelprobleem moet worden opgelost voordat het oorspronkelijke probleem kan worden opgelost, verdient het onthouden van geheugen de voorkeur, omdat een deelprobleem lui wordt opgelost, d.w.z. dat alleen de benodigde berekeningen worden uitgevoerd.
6: Waar wordt memoisatie gebruikt?
Memoiseren is een optimalisatietechniek die wordt gebruikt om computerprogramma's te versnellen door de resultaten van dure functieaanroepen in het cachegeheugen op te slaan en deze terug te sturen wanneer dezelfde invoer opnieuw wordt aangetroffen.
7: Waarom heet het memoriseren?
De term memoisatie komt van het Latijnse woord memorandum (herinneren), dat in het Amerikaans-Engels vaak wordt afgekort tot memo, en wat betekent dat de resultaten van een functie worden omgezet in iets om te onthouden.
8: Hoe vermindert het onthouden van tijdcomplexiteit?
Het steeds opnieuw oplossen van hetzelfde probleem kost tijd en verhoogt de runtime-complexiteit van het totale programma. Dit probleem kan worden opgelost door een cache of geheugen aan te houden waarin we het reeds berekende resultaat van het probleem voor een bepaalde invoer opslaan. Zodat als we hetzelfde probleem niet opnieuw willen berekenen, we eenvoudigweg het resultaat kunnen gebruiken dat in het geheugen is opgeslagen en de tijdscomplexiteit kunnen verminderen.
9: Wat is het verschil tussen memoiseren en caching?
Memoiseren is eigenlijk een specifiek type caching waarbij de retourwaarde van een functie op basis van invoer in de cache wordt opgeslagen. Caching is een algemenere term. HTTP-caching is bijvoorbeeld caching, maar geen memoriseren.
10: Waarom is tabelleren sneller dan memoriseren?
Tabelleren gaat meestal sneller dan memoriseren, omdat het iteratief is en het oplossen van subproblemen geen overhead van recursieve oproepen vereist.
Memoiseren is een techniek die in de computerwetenschappen wordt gebruikt om de uitvoering van recursieve of computationeel dure functies te versnellen door de resultaten van functieaanroepen in het cachegeheugen op te slaan en de in het cachegeheugen opgeslagen resultaten terug te sturen wanneer dezelfde invoer opnieuw optreedt.
Het basisidee van memoisatie is om de uitvoer van een functie op te slaan voor een gegeven reeks invoer en het in de cache opgeslagen resultaat terug te geven als de functie opnieuw wordt aangeroepen met dezelfde invoer. Deze techniek kan rekentijd besparen, vooral voor functies die vaak worden aangeroepen of een hoge tijdscomplexiteit hebben.
Hier is een stapsgewijze handleiding voor het implementeren van memoisatie:
aanwijzingen in c
Identificeer de functie die u wilt optimaliseren met behulp van memoisatie. Deze functie zou herhaalde en dure berekeningen voor dezelfde invoer moeten hebben.
Maak een woordenboekobject om de in de cache opgeslagen resultaten van de functie op te slaan. De sleutels van het woordenboek moeten de invoerparameters voor de functie zijn, en de waarden moeten de berekende resultaten zijn.
Controleer aan het begin van de functie of de invoerparameters al aanwezig zijn in het cachewoordenboek. Als dit het geval is, retourneert u het in de cache opgeslagen resultaat.
Als de invoerparameters niet in het cachewoordenboek staan, berekent u het resultaat en slaat u dit op in het cachewoordenboek met de invoerparameters als sleutel.
Retourneer het berekende resultaat.
Hier is een Python-codevoorbeeld van het implementeren van memoisatie met behulp van een woordenboek:
Python3
def> fibonacci(n, cache>=>{}):> >if> n>in> cache:> >return> cache[n]> >if> n>=>=> 0>:> >result>=> 0> >elif> n>=>=> 1>:> >result>=> 1> >else>:> >result>=> fibonacci(n>->1>)>+> fibonacci(n>->2>)> >cache[n]>=> result> >return> result> |
>
>Uitvoer
>
In de bovenstaande code definiëren we een functie genaamd fibonacci die het n-de getal in de Fibonacci-reeks berekent. We gebruiken een woordenboekobject genaamd cache om de resultaten van de functieaanroepen op te slaan. Als de invoerparameter n al aanwezig is in het cachewoordenboek, retourneren we het in de cache opgeslagen resultaat. Anders berekenen we het resultaat met behulp van recursieve aanroepen van de fibonacci-functie en slaan we het op in het cachewoordenboek voordat we het retourneren.
Memoisatie kan worden gebruikt om de prestaties van veel functies die herhaalde en dure berekeningen vereisen, te optimaliseren. Door de resultaten van functieaanroepen in het cachegeheugen op te slaan, kunnen we onnodige berekeningen vermijden en de uitvoering van de functie versnellen.
Conclusie
Memoiseren is een programmeerconcept en kan op elke programmeertaal worden toegepast. Het absolute doel is om het programma te optimaliseren. Meestal treedt dit probleem op wanneer programma's zware berekeningen uitvoeren. Deze techniek slaat alle eerdere berekende resultaten op in de cache, zodat deze voor hetzelfde probleem niet opnieuw hoeven te worden berekend.
Gerelateerde artikelen:
- Memoriseren met behulp van decorateurs in Python
- JavaScript-memorisatie
