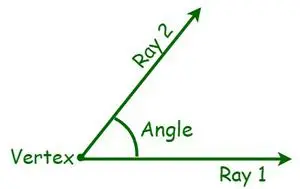
In de meetkunde is een hoek een essentiële maatstaf voor een geometrische vorm. Een hoek wordt gedefinieerd als de mate van rotatie rond het snijpunt tussen twee lijnen of vlakken die nodig is om de ene met de andere in overeenstemming te brengen. Er zijn verschillende soorten hoeken, gebaseerd op het meten van een hoek. Het wordt gemeten in graden of radialen. Een hoek is een vorm die wordt gevormd door twee lijnen of stralen die divergeren vanuit een gemeenschappelijk punt dat een hoekpunt wordt genoemd. Wanneer twee stralen elkaar snijden, d.w.z. wanneer halve lijnen worden geprojecteerd met een gemeenschappelijk eindpunt, wordt een hoek gevormd. Nu worden de gemeenschappelijke eindpunten hoekpunten genoemd, terwijl de stralen bekend staan als de armen.
Soorten hoeken

- Scherpe hoek: Een scherpe hoek is een hoek die groter is dan 0 graden en kleiner dan 90 graden, d.w.z. deze varieert van 0° tot 90° (beide exclusief).
- Juiste hoek: Een rechte hoek wordt de hoek genoemd die precies 90 graden meet.
- Stompe hoek: Een stompe hoek is een hoek die groter is dan 90 graden en kleiner dan 180 graden, d.w.z. deze varieert van 90° tot 180° (beide exclusief).
- Rechte hoek: Een rechte hoek wordt een hoek genoemd die precies 180 graden meet.
- Reflexhoek: Een reflexhoek is een hoek die groter is dan 180 graden en kleiner dan 360 graden, d.w.z. deze varieert van 180° tot 360° (beide exclusief).
- Een volledige hoek of volledige rotatie: Een volledige hoek wordt de hoek genoemd die precies 360 graden meet.
Er zijn ook andere soorten hoeken, zoals complementaire hoeken, aanvullende hoeken en aangrenzende en niet-aangrenzende hoeken.
- Complementaire hoeken: Van twee hoeken wordt gezegd dat ze complementair zijn als hun som een rechte hoek is, dat wil zeggen 90°.
- Aanvullende hoeken: Van twee hoeken wordt gezegd dat ze aanvullend zijn als hun som gelijk is aan 180°.
- Aangrenzende hoeken: Van twee hoeken wordt gezegd dat ze aangrenzend zijn als ze een gemeenschappelijk hoekpunt en een gemeenschappelijke arm delen.
- Niet-aangrenzende hoeken: Van twee hoeken wordt gezegd dat ze niet aan elkaar grenzen als ze geen gemeenschappelijk hoekpunt en een gemeenschappelijke arm delen.
De formule voor het vinden van hoeken
Er zijn verschillende soorten formules voor het vinden van een hoek; sommigen daarvan zijn de centrale hoekformule, de dubbele hoekformule, de halve hoekformule, de samengestelde hoekformule, de binnenhoekformule, enz.
- We gebruiken de formule voor de centrale hoek om de hoek te bepalen van een segment dat in een cirkel is gemaakt.
- We gebruiken de som van de formule voor binnenhoeken om de ontbrekende hoek in een veelhoek te bepalen.
- We gebruiken de trigonometrische verhoudingen om de ontbrekende hoek van een rechthoekige driehoek te vinden.
- We gebruiken de wet van de sinussen of de wet van de cosinus om de ontbrekende hoek van een niet-rechthoekige driehoek te vinden.
Naam van de formule | Formule | Hoe vind je een onbekende hoek? |
|---|---|---|
| Formule voor centrale hoek | θ =(s × 360°)/2prHier is s de booglengte en r de straal van de cirkel | Vervang de waarden van de booglengte en de straal van de cirkel om de hoek te bepalen van een segment dat in een cirkel is gemaakt. |
| Som van formule voor binnenhoeken | 180°(n-2)Hier is n het aantal zijden van een veelhoek | Om de onbekende binnenhoek van een veelhoek te bepalen, berekent u eerst de som van alle binnenhoeken met behulp van deze formule en trekt u vervolgens de som van alle bekende hoeken van het resultaat af. |
| Trigonometrische verhoudingen | sin θ = tegenoverliggende zijde/hypotenusacos θ = aangrenzende zijde/hypotenusatan θ = tegenoverliggende zijde/aangrenzende zijde | Afhankelijk van de beschikbare twee zijden van een rechthoekige driehoek, kiest u een van deze goniometrische verhoudingen om de onbekende hoek te vinden. |
| Wet van sinussen | a/zonde A = b/zonde B = c/zonde CHier zijn A, B en C de binnenhoeken van een driehoek en zijn a, b en c hun respectieve tegenoverliggende zijden. | Als we twee zijden en een niet-ingesloten hoek (of) twee hoeken en een niet-ingesloten zijde kennen, kan de sinuswet worden gebruikt om de onbekende hoeken van een driehoek te bepalen. |
| Wet van cosinus | A2= geb2+ c2– 2bc cos AB2= c2+ een2– 2ca cos BC2= een2+ b2– 2ab cos CHier zijn A, B en C de binnenhoeken van een driehoek en zijn a, b en c hun respectievelijke tegenoverliggende zijden. | Als we drie zijden (of) twee zijden en een ingesloten hoek kennen, kan de cosinusregel worden gebruikt om de onbekende hoeken van een driehoek te bepalen. |
Voorbeeldvragen
Vraag 1: Vind de hoek bij het hoekpunt B van de gegeven driehoek met behulp van een van de goniometrische formules voor het vinden van hoeken.

Oplossing:
Gegeven,
BC = 3 eenheden = aangrenzende zijde van θ.
AC = 4 eenheden = tegenoverliggende zijde van θ.
In dit geval kennen we zowel de tegenoverliggende als de aangrenzende zijden van θ. Daarom kunnen we de raaklijnformule gebruiken om θ te vinden.
⇒ tan θ = tegenoverliggende zijde/aangrenzende zijde
⇒ bruin θ = 4/3
⇒ θ = bruin-1(4/3) ⇒ θ = 53,1°
De hoek bij hoekpunt B is dus 53,1°.
Vraag 2: Bereken de hoeken bij de hoekpunten X en Y, als ∠Z = 35° en x = 3 inch, y = 8 inch en z = 3,5 inch.

Oplossing:
Gegeven,
∠Z = 35° en x = 6 inch, y = 3 inch en z = 3,5 inch
Omdat we alle drie de zijden en een hoek kennen, kunnen we de sinusregelformule gebruiken.
Van de sinusregelformule hebben we
x/sin X = y/sin Y = z/sin Z
Nu,
y/sin Y = z/sin Z
⇒ 3/sin Y = 3,5/sin 35°
css vetgedrukt⇒ 3/zonder Y = 3,5/0,574 {Aangezien zonde 35° = 0,574}
⇒ zonde Y = 3 × (0,574/3,5) = 0,492
⇒ ∠Y = zonde−1(0,492) = 29,47°
We weten dat de som van drie hoeken in een driehoek 180° is.
⇒ ∠X + ∠Y + ∠Z = 180°
⇒ ∠X + 29,47° + 35° = 180°
⇒ ∠X = 180° – 64,47° = 115,53°
Dus ∠X = 115,53° en ∠Y = 29,47°.
Vraag 3: Bereken de vijfde binnenhoek van een vijfhoek als vier binnenhoeken 110°, 85°, 136° en 105° zijn.
Oplossing:
Het aantal zijden van een vijfhoek (n) = 5.
Nu is de som van alle 5 binnenhoeken van een vijfhoek = 180 (n -2)°
= 180 (5 – 2)° = 540°.
De som van de gegeven 4 binnenhoeken = 110°+ 85°+ 136°+ en 105°= 436°.
Dus de vijfde binnenhoek = 540° – 436° = 104°
De vijfde binnenhoek van een vijfhoek is dus 104°.
Vraag 4: Bepaal de waarde van y en ook de maat van de hoeken in de gegeven figuur.

Oplossing:
Uit de gegeven figuur kunnen we opmaken dat (4y – 6)° en (3y + 5)° complementaire hoeken zijn, dat wil zeggen dat de som van (4y – 6)° en (3y + 5)° 90 is. °.
⇒ (4y – 6)° + (3y + 5)° = 90°
⇒ (7y – 1)° = 90°
⇒ 7y = 90° + 1° = 91°
⇒ y = 91°/7 = 13°
Nu, (4y – 6)° = (4 ×13 – 6)° = (52 – 6)° = 46°
(3y + 5)° = (3 × 13 + 5)° = (39 + 5)° = 44°
Vraag 5: Vind de hoek bij hoekpunt Q in de gegeven driehoek met behulp van een van de formules voor het vinden van hoeken.

Oplossing:
Gegeven: p = QR = 6 cm, q = PR = 9 cm, en r = PQ = 7 cm.
Omdat we alle drie de zijden en een hoek kennen, kunnen we de formule van de cosinusregel gebruiken om het hoekpunt Q te vinden.
⇒ q2= blz2+ r2– 2pr cos Q
⇒ 92= 62+ 72– 2 (6)(7) cos Q
⇒ 81 = 36 + 49 – 84 cos Q
⇒ 81 = 85 – 84cos Q
⇒84 cos Q = 81 – 85
⇒ 84 cos Q = -4
⇒ cos Q = -4/84 = -1/21
⇒ ∠Q = cos-1(-1/21) = 92,72°
Daarom is de hoek bij hoekpunt Q, ∠Q = 92,72°.
Vraag 6: Bereken de hoek van een segment gemaakt in een cirkel als de booglengte 12π is en de straal 9 cm.
Oplossing:
Gegeven,
wat is een gebruikersnaamDe booglengte= 12π
Straal (r) = 9 cm
De hoekformule is nu:
⇒ θ = (s×360°)/2pr
⇒ θ = (12π × 360°)/(2π × 5)
⇒ θ =12 ×360°/10
⇒ θ = 240°
De hoek is dus 240°.
