Het volume van een driehoekige piramide wordt gevonden met behulp van de formule V = 1/3A.H . Een driehoekige piramide, ook wel tetraëder genoemd, is een soort piramide met een driehoekige basis en drie driehoekige vlakken die samenkomen op een enkel punt dat de top wordt genoemd.

In dit artikel zullen we in detail leren over piramidedefinitie, driehoekige piramidedefinitie, driehoekige piramideformule, voorbeelden en andere.

Inhoudsopgave

• Wat is een piramide?
• Driehoekige piramidedefinitie
• Driehoekige piramideformule
• Oppervlakte van een driehoekige piramide
• Volume van een driehoekige piramide

Wat is een piramide?

A piramide wordt ingedeeld in verschillende soorten op basis van de vorm van de basis, zoals een driehoekige piramide, een vierkante piramide, een vijfhoekige piramide, een zeshoekige piramide, enz. Een top is een ontmoetingspunt van de zijvlakken of de zijvlakken van een piramide . De loodrechte afstand van de top van een piramide tot het midden van de basis is de hoogte of hoogte van een piramide. De loodrechte afstand tussen de top en de basis van een schuin zijoppervlak van een piramide.

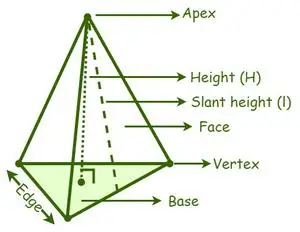
Piramide

Driehoekige piramidedefinitie

Driehoekige piramide is een piramide met een driehoek als basis. Het is ook bekend als een tetraëder en heeft drie driehoekige vlakken en één driehoekige basis, waarbij de driehoekige basis scalair, gelijkbenig of een gelijkzijdige driehoek kan zijn. Een driehoekige piramide wordt verder onderverdeeld in drie typen, namelijk een regelmatige driehoekige piramide, een onregelmatige driehoekige piramide en een rechthoekige driehoekige piramide.

• Regelmatige driehoekige piramide: Een driehoekige piramide waarvan de vier vlakken gelijkzijdige driehoeken zijn, wordt een regelmatige driehoekige piramide genoemd. Omdat de piramide uit gelijkzijdige driehoeken bestaat, is de maat van al zijn interne hoeken 60°.

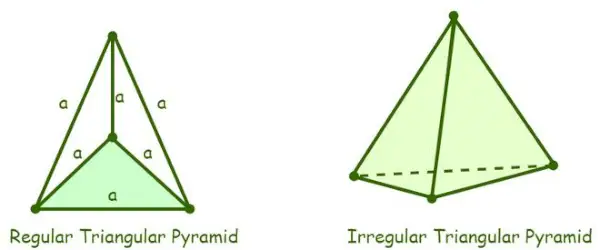
Driehoekige piramidedefinitie

• Onregelmatige driehoekige piramide: Een onregelmatige driehoekige piramide is een piramide waarvan de randen van de basis niet gelijk zijn, dat wil zeggen dat de basis van een onregelmatige driehoekige piramide een ongelijkbenige driehoek of een gelijkbenige driehoek is. Er wordt aangenomen dat alle driehoekige piramides regelmatige driehoekige piramides zijn, tenzij een driehoekige piramide specifiek als onregelmatig wordt vermeld.

• Rechte driehoekige piramide: Een rechthoekige driehoekige piramide is een piramide waarvan de basis een rechthoekige driehoek is en waarvan de top is uitgelijnd boven het midden van de basis.

Driehoekige piramideformule

Er zijn twee formules voor een driehoekige piramide: de oppervlakte van een driehoekige piramide en het volume van een driehoekige piramide.

• Oppervlakte van een driehoekige piramide
  • Laterale oppervlakte van een driehoekige piramide
  • Totale oppervlakte van een driehoekige piramide
• Volume van een driehoekige piramide

Oppervlakte van een driehoekige piramide

Oppervlakte van een piramide kent twee soorten oppervlakten, namelijk: de laterale oppervlakte en de totale oppervlakte, waarbij de oppervlakte van een piramide de som is van de oppervlakten van de zijvlakken, of zijvlakken, en de basisoppervlakte. van een piramide.

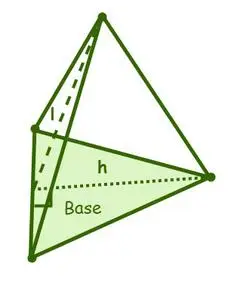
Oppervlakte van een driehoekige piramide

Laterale oppervlakte van een driehoekige piramide

Het laterale oppervlak van een driehoekige piramide wordt berekend met behulp van de formule:

binair zoeken in Java

Lateraal oppervlak van een driehoekige piramide (LSA) = ½ x omtrek x schuine hoogte

Totale oppervlakte van een driehoekige piramide

De totale oppervlakte van een piramide (TSA) = Zijoppervlakte van de piramide + Oppervlakte van de basis

Dus TSA = ½ × omtrek × schuine hoogte + ½ × basis × hoogte

Totale oppervlakte van een driehoekige piramide (TSA) = ½ × P × l + ½ bh

waar,

• P is de omtrek van de basis
• l is de schuine hoogte van de piramide
• B is de basis van de driehoek aan de basis
• H is Hoogte van de piramide

Volume van een driehoekige piramide

Het volume van een piramide is de totale ruimte tussen alle vlakken van een piramide. Het volume van een piramide wordt doorgaans weergegeven door de letter V, en de formule is gelijk aan een derde van het product van het basisoppervlak en de hoogte van de piramide.

De formule voor het volume van een piramide wordt als volgt gegeven:

Volume van een driehoekige piramide = 1/3 × basisoppervlak × hoogte

V = 1/3 × AH kubieke eenheden

waar,

• IN is het volume van de piramide
• A is het gebied van de basis van een piramide
• H is de hoogte of hoogte van een piramide

De formule voor het volume van een regelmatige driehoekige piramide wordt als volgt gegeven

Volume van regelmatige driehoekige piramide = a ³ /6√2 kubieke eenheden

Waar A isLengte van randen

Artikel gerelateerd aan Driehoekige piramide:

• Rechthoekige piramide
• Vierkante piramide
• Vijfhoekige piramide
• Zeshoekige piramide
• Volume van een piramideformule
• Oppervlakte van een piramideformule

Voorbeelden van de driehoekige piramideformule

Voorbeeld 1: Bepaal het volume van een driehoekige piramide waarvan het basisoppervlak en de hoogte 50 cm zijn ² en 12 cm respectievelijk.

Oplossing:

Gezien gegevens,

• Oppervlakte van de driehoekige basis = 100 cm²
• Hoogte van de piramide = 12 cm

We weten dat,

abstracte klasse Java

Volume van een driehoekige piramide (V) = 1/3 × Oppervlakte van de driehoekige basis × Hoogte

H = 1/3 × 50 × 12 = 200cm³

Het volume van de gegeven driehoekige piramide is dus 200 cm³.

Voorbeeld 2: Zoek de totale oppervlakte van een regelmatige driehoekige piramide wanneer de lengte van elke rand 20 cm is.

Oplossing:

Gezien gegevens,

• Lengte van elke rand van een regelmatige driehoekige piramide (a) = 8 inch

We weten dat,

Totale oppervlakte van een regelmatige driehoekige piramide = √3a²

⇒ TSA = √3 × 8²

= 64√3 = 110,851 vierkante meter

De totale oppervlakte van een regelmatige driehoekige piramide is dus 110,851 vierkante meter.

Voorbeeld 3: Bepaal het volume van een regelmatige driehoekige piramide als de lengte van de rand 10 cm is.

Oplossing:

Gezien gegevens,

• Lengte van elke rand van een regelmatige driehoekige piramide (a) = 10 cm

We weten dat,

Volume van een regelmatige driehoekige piramide = a³/6√2

⇒ V = (10)³/6√2

= 1000/6√2 = 117,85 cm³

Het volume van een regelmatige driehoekige piramide is dus 117,85 cu. cm.

Voorbeeld 4: Bepaal de schuine hoogte van de driehoekige piramide als het laterale oppervlak 600 vierkante meter is en de omtrek van de basis 60 inch is.

Oplossing:

Gezien gegevens,

• Zijoppervlakte = 600 vierkante meter
• Omtrek van de basis = 60 inch

We weten dat,

converteer char naar int java

Zijoppervlakte = ½ × omtrek × schuine hoogte

600 = ½ × 60 × l

l = 600/30 = 20 inch

Daarom is de schuine hoogte van de gegeven piramide 20 inch.

Voorbeeld 5: Bepaal de totale oppervlakte van een driehoekige piramide waarvan het basisoppervlak 28 vierkante cm is, de omtrek van de driehoek 18 cm is en de schuine hoogte van de piramide 20 cm is.

Oplossing:

Gezien gegevens,

• Oppervlakte driehoekige basis = 28 cm²
• Schuine hoogte (l) = 20 cm
• Omtrek (P) = 18 cm

We weten dat,

hippe computertaal

Totale oppervlakte (TSA) van een driehoekige piramide = ½ × omtrek × schuine hoogte + basisoppervlak

⇒ TSA = ½ × 18 × 20 + 28

= 180 + 28 = 208 vierkante cm

De totale oppervlakte van de gegeven piramide is dus 208 vierkante cm.

Oefenproblemen met de driehoekige piramideformule

Q1. Gegeven een driehoekige piramide met een basisoppervlak van 15 vierkante eenheden en een hoogte van 10 eenheden, wat is dan het volume van de piramide?

Vraag 2. Gegeven een regelmatige driehoekige piramide waarbij elke rand van de gelijkzijdige driehoekige basis 6 eenheden meet, wat is dan de totale oppervlakte van de piramide?

Q3. Gegeven een regelmatige driehoekige piramide waarbij elke rand van de gelijkzijdige driehoekige basis 4 eenheden meet en een hoogte van 5 eenheden, wat is dan het volume en de totale oppervlakte van de piramide?

Q4. Als de zijdelengten van de basis van een driehoekige piramide 3 eenheden, 4 eenheden en 5 eenheden zijn, en de hoogte van de piramide 12 eenheden is, wat is dan het volume van de piramide?

Vraag 5. Voor een driehoekige piramide met een basis in de vorm van een rechthoekige driehoek met poten van 3 eenheden en 4 eenheden, en hypotenusa van 5 eenheden, wat is de totale oppervlakte als de hoogte van de piramide vanaf de basis tot de top 10 eenheden is ?

Veelgestelde vragen over de driehoekige piramideformule

Wat is de definitie van een driehoekige piramide?

Een driehoekige piramide is een geometrische vorm met een driehoekige basis en drie driehoekige vlakken, met een gemeenschappelijk hoekpunt.

Hoeveel vlakken en hoekpunten heeft een driehoekige piramide?

Driehoekige piramide heeft vier vlakken en vier hoekpunten. Eén hoekpunt is gemeenschappelijk voor alle drie de vlakken van de piramide.

Wat is de basisformule voor een piramide?

Basisformules van een piramide zijn:

• LSA = ½ × omtrek × schuine hoogte
• TSA = ½ × P × l + ½ bh
• V = 1/3 × Ah

Wat zijn soorten driehoekige piramides?

Er zijn drie soorten driehoekige piramides

• Regelmatige driehoekige piramide
• Onregelmatige driehoekige piramide
• Rechthoekige driehoekige piramide

Wat is de formule voor driehoeken?

De formule voor de oppervlakte van een driehoek is:

• (Oppervlak)A = 1/2 × b × h