In dit artikel bespreken we het doorlopen van bomen in de datastructuur. De term 'boomtraversal' betekent het doorkruisen of bezoeken van elk knooppunt van een boom. Er is één manier om de lineaire gegevensstructuur te doorkruisen, zoals de gekoppelde lijst, de wachtrij en de stapel. Terwijl er meerdere manieren zijn om een boom te doorkruisen, die als volgt worden vermeld:
- Doortocht vooraf bestellen
- In volgorde doorkruisen
- Het passeren van postwissels
Daarom bespreken we in dit artikel de hierboven genoemde technieken voor het doorkruisen van een boom. Laten we nu beginnen met het bespreken van de manieren waarop bomen worden doorkruist.
Doortocht vooraf bestellen
Deze techniek volgt het 'root left right'-beleid. Het betekent dat het eerste hoofdknooppunt wordt bezocht, waarna de linker subboom recursief wordt doorlopen, en ten slotte de rechter subboom recursief wordt doorlopen. Omdat het hoofdknooppunt vóór (of vóór) de linker en rechter subboom wordt doorlopen, wordt dit preorder-traversal genoemd.
Bij een pre-order-traversal wordt dus elk knooppunt vóór beide subbomen bezocht.
De toepassingen van pre-order traversal omvatten -
- Het wordt gebruikt om een kopie van de boom te maken.
- Het kan ook worden gebruikt om de voorvoegselexpressie van een expressieboom op te halen.
Algoritme
Until all nodes of the tree are not visited Step 1 - Visit the root node Step 2 - Traverse the left subtree recursively. Step 3 - Traverse the right subtree recursively.
Voorbeeld
Laten we nu eens kijken naar het voorbeeld van de pre-order traversal-techniek.
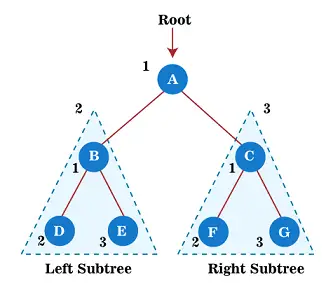
Begin nu met het toepassen van de preorder-traversal op de bovenstaande boom. Eerst doorkruisen we het hoofdknooppunt A; ga daarna naar de linker subboom B , die ook in pre-order zal worden doorlopen.
Dus voor de linkerdeelboom B: eerst het hoofdknooppunt B wordt zelf doorkruist; daarna de linker subboom D wordt doorkruist. Sinds knooppunt D heeft geen kinderen, ga naar de rechter subboom EN . Omdat knooppunt E ook geen kinderen heeft, is het doorlopen van de linker deelboom van hoofdknooppunt A voltooid.
wat is svn afrekenen
Ga nu naar de rechter subboom van hoofdknooppunt A, dat wil zeggen C. Dus, voor rechter subboom C, eerst het hoofdknooppunt C heeft zichzelf doorkruist; daarna de linker subboom F wordt doorkruist. Sinds knooppunt F geen kinderen heeft, ga naar de rechter subboom G . Omdat knooppunt G ook geen kinderen heeft, is het doorlopen van de rechter deelboom van hoofdknooppunt A voltooid.
Daarom worden alle knooppunten van de boom doorlopen. Dus de uitvoer van de pre-order-doorgang van de bovenstaande boom is -
A → B → D → E → C → F → G
string.format Java-tekenreeks
Als u meer wilt weten over de pre-order-traversal in de datastructuur, kunt u de link volgen Doortocht vooraf bestellen .
Het passeren van postwissels
Deze techniek volgt het 'links-rechts root'-beleid. Het betekent dat de eerste linker subboom van het hoofdknooppunt wordt doorlopen, daarna recursief de rechter subboom doorkruist en ten slotte het hoofdknooppunt wordt doorlopen. Omdat het hoofdknooppunt na (of na) de linker en rechter subboom wordt doorlopen, wordt dit postorder-traversal genoemd.
Bij een postorder-traversal wordt dus elk knooppunt na zijn beide subbomen bezocht.
De toepassingen van postorder traversal omvatten -
- Het wordt gebruikt om de boom te verwijderen.
- Het kan ook worden gebruikt om de postfix-expressie van een expressieboom op te halen.
Algoritme
Until all nodes of the tree are not visited Step 1 - Traverse the left subtree recursively. Step 2 - Traverse the right subtree recursively. Step 3 - Visit the root node.
Voorbeeld
Laten we nu eens kijken naar het voorbeeld van de postorder traversal-techniek.

Begin nu met het toepassen van de postorder-traversal op de bovenstaande boom. Eerst doorkruisen we de linker subboom B die in de postvolgorde zal worden doorlopen. Daarna zullen we de rechter subboom doorkruisen C in postorder. En tenslotte het wortelknooppunt van de bovenstaande boom, d.w.z. A , wordt doorkruist.
Dus voor de linker deelboom B: eerst de linker deelboom D wordt doorkruist. Sinds knooppunt D geen kinderen heeft, doorloopt u de rechter deelboom EN . Omdat knooppunt E ook geen kinderen heeft, ga je naar het hoofdknooppunt B. Na het passeren van knooppunt B, het doorlopen van de linker subboom van hoofdknooppunt A is voltooid.
Ga nu naar de rechter deelboom van hoofdknooppunt A, dat wil zeggen C. Dus voor de rechter deelboom C, eerst de linker deelboom F wordt doorkruist. Sinds knooppunt F geen kinderen heeft, doorloopt u de rechter deelboom G . Omdat knooppunt G ook geen kinderen heeft, dus uiteindelijk het hoofdknooppunt van de rechter deelboom, d.w.z. C, wordt doorkruist. Het doorlopen van de rechter subboom van hoofdknooppunt A is voltooid.
Doorkruis ten slotte het hoofdknooppunt van een bepaalde boom, d.w.z. A . Nadat het hoofdknooppunt is doorlopen, is de postorder-doorgang van de gegeven boom voltooid.
Daarom worden alle knooppunten van de boom doorlopen. Dus de uitvoer van de postorder-doorgang van de bovenstaande boom is -
D → E → B → F → G → C → A
Als u meer wilt weten over de postorder-traversal in de datastructuur, kunt u de link volgen Het passeren van postwissels .
In volgorde doorkruisen
Deze techniek volgt het 'left root right'-beleid. Het betekent dat de eerste linker subboom wordt bezocht nadat dat hoofdknooppunt is doorlopen, en ten slotte de rechter subboom. Wanneer het hoofdknooppunt tussen de linker en rechter subboom wordt doorlopen, wordt het in volgorde traversal genoemd.
Bij de inorder-traversal wordt dus elk knooppunt tussen zijn subbomen bezocht.
De toepassingen van Inorder-traversal omvatten -
hoop sorteren
- Het wordt gebruikt om de BST-knooppunten in oplopende volgorde te krijgen.
- Het kan ook worden gebruikt om de voorvoegselexpressie van een expressieboom op te halen.
Algoritme
Until all nodes of the tree are not visited Step 1 - Traverse the left subtree recursively. Step 2 - Visit the root node. Step 3 - Traverse the right subtree recursively.
Voorbeeld
Laten we nu eens kijken naar het voorbeeld van de Inorder-traversaltechniek.

Begin nu met het toepassen van de inorder-traversal op de bovenstaande boom. Eerst doorkruisen we de linker deelboom B die in volgorde zal worden doorlopen. Daarna zullen we het hoofdknooppunt doorkruisen A . En tot slot de juiste subboom C wordt in volgorde doorlopen.
Dus voor de linker subboom B , eerst de linker subboom D wordt doorkruist. Sinds knooppunt D heeft geen kinderen, dus na het doorkruisen, knooppunt B zal worden doorlopen, en uiteindelijk de rechter subboom van knooppunt B EN , wordt doorkruist. Knooppunt E heeft ook geen kinderen; daarom is het doorlopen van de linker subboom van hoofdknooppunt A voltooid.
Ga daarna door het hoofdknooppunt van een bepaalde boom, d.w.z. A .
Ga ten slotte naar de rechter deelboom van hoofdknooppunt A, dat wil zeggen C. Dus voor de rechter deelboom C; eerst de linkerdeelboom F wordt doorkruist. Sinds knooppunt F heeft geen kinderen, node C zal worden doorlopen, en uiteindelijk een rechter deelboom van knooppunt C, dat wil zeggen: G , wordt doorkruist. Knooppunt G heeft ook geen kinderen; daarom is het doorlopen van de rechter deelboom van hoofdknooppunt A voltooid.
Terwijl alle knooppunten van de boom worden doorlopen, is het in volgorde doorlopen van de gegeven boom voltooid. De uitvoer van de inorder-doorgang van de bovenstaande boom is -
D → B → E → A → F → C → G
logica van de eerste orde
Als u meer wilt weten over de inorder-traversal in de datastructuur, kunt u de link volgen Inorder-traversal .
Complexiteit van technieken voor het doorkruisen van bomen
De tijdscomplexiteit van de hierboven besproken technieken voor het doorlopen van bomen is: Op) , waar 'N' is de grootte van een binaire boom.
Terwijl de hierboven besproken ruimtecomplexiteit van technieken voor het doorkruisen van bomen dat wel is O(1) als we geen rekening houden met de stapelgrootte voor functieaanroepen. Anders is de ruimtecomplexiteit van deze technieken dat wel Oh) , waar 'H' is de hoogte van de boom.
Implementatie van Tree Traversal
Laten we nu eens kijken naar de implementatie van de hierboven besproken technieken met behulp van verschillende programmeertalen.
Programma: Schrijf een programma om boomtraversaltechnieken te implementeren in C.
#include #include struct node { int element; struct node* left; struct node* right; }; /*To create a new node*/ struct node* createNode(int val) { struct node* Node = (struct node*)malloc(sizeof(struct node)); Node->element = val; Node->left = NULL; Node->right = NULL; return (Node); } /*function to traverse the nodes of binary tree in preorder*/ void traversePreorder(struct node* root) { if (root == NULL) return; printf(' %d ', root->element); traversePreorder(root->left); traversePreorder(root->right); } /*function to traverse the nodes of binary tree in Inorder*/ void traverseInorder(struct node* root) { if (root == NULL) return; traverseInorder(root->left); printf(' %d ', root->element); traverseInorder(root->right); } /*function to traverse the nodes of binary tree in postorder*/ void traversePostorder(struct node* root) { if (root == NULL) return; traversePostorder(root->left); traversePostorder(root->right); printf(' %d ', root->element); } int main() { struct node* root = createNode(36); root->left = createNode(26); root->right = createNode(46); root->left->left = createNode(21); root->left->right = createNode(31); root->left->left->left = createNode(11); root->left->left->right = createNode(24); root->right->left = createNode(41); root->right->right = createNode(56); root->right->right->left = createNode(51); root->right->right->right = createNode(66); printf('
The Preorder traversal of given binary tree is -
'); traversePreorder(root); printf('
The Inorder traversal of given binary tree is -
'); traverseInorder(root); printf('
The Postorder traversal of given binary tree is -
'); traversePostorder(root); return 0; } Uitvoer

Programma: Schrijf een programma om boomtraversaltechnieken in C# te implementeren.
using System; class Node { public int value; public Node left, right; public Node(int element) { value = element; left = right = null; } } class BinaryTree { Node root; BinaryTree() { root = null; } void traversePreorder(Node node) { if (node == null) return; Console.Write(node.value + ' '); traversePreorder(node.left); traversePreorder(node.right); } void traverseInorder(Node node) { if (node == null) return; traverseInorder(node.left); Console.Write(node.value + ' '); traverseInorder(node.right); } void traversePostorder(Node node) { if (node == null) return; traversePostorder(node.left); traversePostorder(node.right); Console.Write(node.value + ' '); } void traversePreorder() { traversePreorder(root); } void traverseInorder() { traverseInorder(root); } void traversePostorder() { traversePostorder(root); } static void Main() { BinaryTree bt = new BinaryTree(); bt.root = new Node(37); bt.root.left = new Node(27); bt.root.right = new Node(47); bt.root.left.left = new Node(22); bt.root.left.right = new Node(32); bt.root.left.left.left = new Node(12); bt.root.left.left.right = new Node(25); bt.root.right.left = new Node(42); bt.root.right.right = new Node(57); bt.root.right.right.left = new Node(52); bt.root.right.right.right = new Node(67); Console.WriteLine('The Preorder traversal of given binary tree is - '); bt.traversePreorder(); Console.WriteLine(); Console.WriteLine('The Inorder traversal of given binary tree is - '); bt.traverseInorder(); Console.WriteLine(); Console.WriteLine('The Postorder traversal of given binary tree is - '); bt.traversePostorder(); } } Uitvoer

Programma: Schrijf een programma om boomtraversaltechnieken in C++ te implementeren.
10 van 10
#include using namespace std; struct node { int element; struct node* left; struct node* right; }; /*To create a new node*/ struct node* createNode(int val) { struct node* Node = (struct node*)malloc(sizeof(struct node)); Node->element = val; Node->left = NULL; Node->right = NULL; return (Node); } /*function to traverse the nodes of binary tree in preorder*/ void traversePreorder(struct node* root) { if (root == NULL) return; cout<<' '<element<left); traversepreorder(root->right); } /*function to traverse the nodes of binary tree in Inorder*/ void traverseInorder(struct node* root) { if (root == NULL) return; traverseInorder(root->left); cout<<' '<element<right); } *function to traverse the nodes of binary tree in postorder* void traversepostorder(struct node* root) { if (root="=" null) return; traversepostorder(root->left); traversePostorder(root->right); cout<<' '<element<left="createNode(28);" root->right = createNode(48); root->left->left = createNode(23); root->left->right = createNode(33); root->left->left->left = createNode(13); root->left->left->right = createNode(26); root->right->left = createNode(43); root->right->right = createNode(58); root->right->right->left = createNode(53); root->right->right->right = createNode(68); cout<<'
the preorder traversal of given binary tree is -
'; traversepreorder(root); cout<<'
inorder traverseinorder(root); postorder traversepostorder(root); return 0; } < pre> <p> <strong>Output</strong> </p> <img src="//techcodeview.com/img/ds-tutorial/17/tree-traversal-inorder-6.webp" alt="Tree Traversal"> <p> <strong>Program:</strong> Write a program to implement tree traversal techniques in Java.</p> <pre> class Node { public int value; public Node left, right; public Node(int element) { value = element; left = right = null; } } class Tree { Node root; /* root of the tree */ Tree() { root = null; } /*function to print the nodes of given binary in Preorder*/ void traversePreorder(Node node) { if (node == null) return; System.out.print(node.value + ' '); traversePreorder(node.left); traversePreorder(node.right); } /*function to print the nodes of given binary in Inorder*/ void traverseInorder(Node node) { if (node == null) return; traverseInorder(node.left); System.out.print(node.value + ' '); traverseInorder(node.right); } /*function to print the nodes of given binary in Postorder*/ void traversePostorder(Node node) { if (node == null) return; traversePostorder(node.left); traversePostorder(node.right); System.out.print(node.value + ' '); } void traversePreorder() { traversePreorder(root); } void traverseInorder() { traverseInorder(root); } void traversePostorder() { traversePostorder(root); } public static void main(String args[]) { Tree pt = new Tree(); pt.root = new Node(36); pt.root.left = new Node(26); pt.root.right = new Node(46); pt.root.left.left = new Node(21); pt.root.left.right = new Node(31); pt.root.left.left.left = new Node(11); pt.root.left.left.right = new Node(24); pt.root.right.left = new Node(41); pt.root.right.right = new Node(56); pt.root.right.right.left = new Node(51); pt.root.right.right.right = new Node(66); System.out.println(); System.out.println('The Preorder traversal of given binary tree is - '); pt.traversePreorder(); System.out.println('
'); System.out.println('The Inorder traversal of given binary tree is - '); pt.traverseInorder(); System.out.println('
'); System.out.println('The Postorder traversal of given binary tree is - '); pt.traversePostorder(); System.out.println(); } } </pre> <p> <strong>Output</strong> </p> <p>After the execution of the above code, the output will be -</p> <img src="//techcodeview.com/img/ds-tutorial/17/tree-traversal-inorder-7.webp" alt="Tree Traversal"> <h2>Conclusion</h2> <p>In this article, we have discussed the different types of tree traversal techniques: preorder traversal, inorder traversal, and postorder traversal. We have seen these techniques along with algorithm, example, complexity, and implementation in C, C++, C#, and java.</p> <p>So, that's all about the article. Hope it will be helpful and informative to you.</p> <hr></'
></'></'></'> Uitvoer
Na de uitvoering van de bovenstaande code zal de uitvoer zijn:

Conclusie
In dit artikel hebben we de verschillende soorten boomtraversaltechnieken besproken: preorder traversal, inorder traversal en postorder traversal. We hebben deze technieken samen met algoritme, voorbeeld, complexiteit en implementatie gezien in C, C++, C# en Java.
Dus dat is alles over het artikel. Ik hoop dat het nuttig en informatief voor u zal zijn.
