Oppervlakte van een prisma: In de wiskunde is een prisma een essentieel lid van de veelvlakkenfamilie en wordt het gedefinieerd als een driedimensionale vorm met twee identieke veelhoeken die naar elkaar toe gericht zijn en die zijdelings verbonden zijn door rechthoekige of parallellogramvlakken. De identieke veelhoeken kunnen driehoeken, vierkanten, rechthoeken, vijfhoeken of elke andere n-zijdige veelhoek zijn en worden de basis van het prisma genoemd. De andere vlakken van een prisma zijn parallellogrammen of rechthoeken.

In dit artikel zullen we bespreken verschillende soorten prisma's, en het oppervlak van de prismaformule, met voorbeelden en oefenproblemen.

Inhoudsopgave

• Wat is het oppervlak van het prisma?
• Verschillende soorten prisma
• Driehoekig Prisma
• Rechthoekig prisma
• Vierkant prisma
• Vijfhoekig prisma
• Zeshoekige Prisma
• Oppervlakte van prismaformule
• Oppervlakte van een prisma Opgeloste voorbeelden
• Oefenproblemen op het oppervlak van een prisma

Wat is het oppervlak van het prisma?

De oppervlakte van een prisma wordt de totale oppervlakte genoemd die door alle vlakken wordt omsloten. Om de oppervlakte van een prisma te bepalen, moeten we de oppervlakten van elk van zijn vlakken berekenen en vervolgens de resulterende gebieden bij elkaar optellen. Een prisma heeft twee soorten oppervlakken, namelijk het laterale oppervlak en het totale oppervlak. Het gebied dat wordt ingenomen door de vlakken van een prisma, met uitzondering van de twee parallelle vlakken (basis van een prisma), wordt het laterale oppervlak genoemd.

Het laterale oppervlak van een prisma = [basisomtrek x hoogte] vierkante eenheden

Nu is de totale oppervlakte van een prisma de som van de oppervlakten van de twee bases en de laterale oppervlakte.

De algemene formule voor het berekenen van de totale oppervlakte van elk type rechter prisma is:

De totale oppervlakte van een prisma = [2 (basisoppervlak) + (basisomtrek x hoogte)] vierkante eenheden

Verschillende soorten prisma

Er zijn verschillende soorten prisma's gebaseerd op de vorm van de basis van een prisma, zoals

• Driehoekige prisma's,
• Vierkante prisma's,
• Rechthoekige prisma's,
• Vijfhoekige prisma's,
• Zeshoekige prisma's,
• Achthoekige prisma's.

Driehoekig Prisma

Een prisma met een driehoekige basis wordt een driehoekig prisma genoemd. Een driehoekig prisma bestaat uit drie schuine rechthoekige oppervlakken en twee evenwijdige driehoekige basissen. Laat H de hoogte van het driehoekige prisma zijn; a, b en c zijn de lengtes van de zijkanten, en h is de hoogte van de driehoekige basissen.

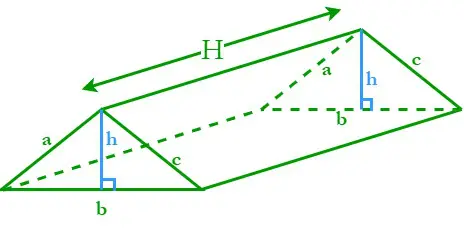
De omtrek van een driehoekige basis (P) = Som van de drie zijden = a + b + c

De oppervlakte van een driehoekige basis (A) = ½ × basis × hoogte = ½ bh

We weten dat de algemene formule voor de Het laterale oppervlak van een rechterprisma is L.S.A. = PH, waarbij P de basisomtrek is en A het basisoppervlak.

Door alle waarden in de algemene formule te vervangen, krijgen we ,

Het zijoppervlak van een driehoekig prisma = (a + b +c)H vierkante eenheden

waar,

a, b, c zijn zijden van een driehoekige basis

H is de hoogte van het driehoekige prisma

We weten dat de algemene formule voor de totale oppervlakte van een recht prisma is: T. S. A. = PH+2A, waarbij P de basisomtrek is, A het basisoppervlak is en H de hoogte van het prisma is.

Door alle waarden in de algemene formule te vervangen, krijgen we

De totale oppervlakte van het driehoekige prisma = (a + b + c)H + 2 × (½ bh)

De totale oppervlakte van het driehoekige prisma = (a + b + c)H + bh vierkante eenheden

waar,

a, b, c zijn zijden van een driehoekige basis

H is de hoogte van het driehoekige prisma

h is de hoogte van de driehoek

Rechthoekig prisma

Een prisma met een rechthoekige basis wordt een rechthoekig prisma genoemd. Een rechthoekig prisma bestaat uit vier rechthoekige oppervlakken en twee evenwijdige rechthoekige bases. Stel dat de hoogte van het prisma h is en de lengte en breedte van de rechthoekige basis respectievelijk l en w .

De omtrek van een rechthoekige basis (P) = Som van de vier zijden = 2 (l + w)

De oppervlakte van een rechthoekige basis (A) = lengte × breedte = l × b

We weten dat de algemene formule voor het laterale oppervlak van een rechter prisma L.S.A. = PH is, waarbij P de basisomtrek is en A het basisoppervlak.

r in c-programmering

Door alle waarden in de algemene formule te vervangen, krijgen we ,

Het zijoppervlak van een rechthoekig prisma = 2h(l + w) vierkante eenheden

waar,

Ik ben lengte

w is breedte

h is hoogte

We weten dat de algemene formule voor het totale oppervlak van een rechter prisma T.S.A. = PH+2A is, waarbij P de basisomtrek is, A het basisoppervlak en H de hoogte van het prisma.

Door alle waarden in de algemene formule te vervangen, krijgen we

De totale oppervlakte van het rechthoekige prisma = 2h(l + w) + 2(l x w)

= 2 liter + 2 wh + 2 liter

De totale oppervlakte van het rechthoekige prisma = 2 (lh + wh + lw) vierkante eenheden

waar,

onderstrepen in afwaardering

Ik ben lengte

w is breedte

h is hoogte

Vierkant prisma

Een prisma met een vierkante basis wordt een vierkant prisma genoemd. Een vierkant prisma bestaat uit vier rechthoekige oppervlakken en twee evenwijdige vierkante basissen. Stel dat de hoogte van het prisma h is en de lengte van de vierkante basis s.

De omtrek van een vierkante basis (P) = Som van de vier zijden = s + s + s + s = 4s

De oppervlakte van een vierkante basis (A) = (lengte van de zijkant)²= s²

We weten dat de algemene formule voor het laterale oppervlak van een rechter prisma L.S.A. = PH is, waarbij P de basisomtrek is en A het basisoppervlak.

Door alle waarden in de algemene formule die we krijgen te vervangen,

Het zijoppervlak van een vierkant prisma = 4sh vierkante eenheden

waar,

s is de zijde van de vierkante basis

h is de hoogte van het vierkante prisma

We weten dat de algemene formule voor de totale oppervlakte van een recht prisma is: T.S.A. = PH+2A, waar P is de basisomtrek, A is het basisoppervlak en H is de hoogte van het prisma.

Door alle waarden in de algemene formule te vervangen, krijgen we

De totale oppervlakte van het vierkante prisma = [4sh + 2s ² ] vierkante eenheden

waar,

s is de zijde van de vierkante basis

h is de hoogte van het vierkante prisma

Vijfhoekig prisma

Een prisma met een vijfhoekige basis wordt een vijfhoekig prisma genoemd. Een vijfhoekig prisma bestaat uit vijf hellende rechthoekige oppervlakken en twee evenwijdige vijfhoekige bases. Laat h de hoogte van het vijfhoekige prisma zijn; a en b zijn de apothema-lengte en zijlengtes van de vijfhoekige basissen.

De omtrek van een vijfhoekige basis (P) = Som van de vijf zijden = 5b

De oppervlakte van een vijfhoekige basis (A) = 5/2 x (apothemlengte) x (lengte van de zijkant) = 5ab

We weten dat de algemene formule voor het laterale oppervlak van een rechter prisma L.S.A. = PH is, waarbij P de basisomtrek is en A het basisoppervlak.

Door alle waarden in de algemene formule die we krijgen te vervangen,

Het zijoppervlak van een vijfhoekig prisma = 5bh vierkante eenheden

waar,

b is de zijde van de vijfhoekige basis

h is de hoogte van een vijfhoekig prisma

We weten dat de algemene formule voor het totale oppervlak van een rechter prisma T.S.A. = PH+2A is, waarbij P de basisomtrek is, A het basisoppervlak en H de hoogte van het prisma.

Door alle waarden in de algemene formule die we krijgen te vervangen,

De totale oppervlakte van het vijfhoekige prisma = [5bh + 5ab] vierkante eenheden

waar,

b is de zijde van de vijfhoekige basis

a is de lengte van de apothema.

h is de hoogte van een vijfhoekig prisma

Zeshoekige Prisma

Een prisma met een zeshoekige basis wordt een zeshoekig prisma genoemd. Een zeshoekig prisma bestaat uit zes schuine rechthoekige oppervlakken en twee evenwijdige zeshoekige bases. Laat h de hoogte van het zeshoekige prisma zijn; a zijn de zijdelengtes van de zeshoekige basissen.

De omtrek van een zeshoekige basis (P) = Som van de zes zijden = 6a

De oppervlakte van een zeshoekige basis (A) = 6 x (oppervlakte van een gelijkzijdige driehoek)

A = 6 x (√3a²/4) ⇒ EEN = 3√3a²/2

We weten dat de algemene formule voor het laterale oppervlak van een rechter prisma L.S.A. = PH is, waarbij P de basisomtrek is en A het basisoppervlak.

Door alle waarden in de algemene formule die we krijgen te vervangen,

Het zijoppervlak van een zeshoekig prisma = 6ah vierkante eenheden

waar,

a is de zijde van een zeshoekige basis

h is de hoogte van de zeshoekige basis

We weten dat de algemene formule voor het totale oppervlak van een rechter prisma T.S.A. = PH+2A is, waarbij P de basisomtrek is, A het basisoppervlak en H de hoogte van het prisma.

Door alle waarden in de algemene formule te vervangen, krijgen we

De totale oppervlakte van het hexagonale prisma = [6ah +3√3a²] vierkante eenheden

waar,

a is de zijde van een zeshoekige basis

h is de hoogte van de zeshoekige basis:

Oppervlakte van prismaformule

De onderstaande tabel bevat de formule voor verschillende soorten prisma's:

Oppervlakte van een prisma Opgeloste voorbeelden

Probleem 1: Wat is de hoogte van een prisma met een basisoppervlak van 36 vierkante eenheden, een basisomtrek van 24 eenheden en een totale oppervlakte van 320 vierkante eenheden?

Oplossing:

Gezien gegevens,

Basisoppervlak = 36 vierkante eenheden

Basisomtrek = 24 eenheden

De totale oppervlakte van het prisma = 320 vierkante eenheden

We hebben,

De totale oppervlakte van het prisma = (2 × basisoppervlak) + (basisomtrek × hoogte)

⇒ 320 = (2 × 36)+ (24 × uur)

⇒ 24 uur = 248 ⇒ uur = 10,34 eenheden

De hoogte van het gegeven prisma is dus 10,34 eenheden.

Probleem 2: Bereken de totale oppervlakte van een vierkant prisma als de hoogte van het prisma en de lengte van de zijkant van de vierkante basis respectievelijk 13 cm en 4 cm zijn.

Oplossing:

Gezien gegevens,

De hoogte van het vierkante prisma (h) = 13 cm

De lengte van de zijkant van de vierkante basis (a) = 4 cm

We weten dat,

De totale oppervlakte van een vierkant prisma = 2a²+ 4ah

= 2× (4)²+ 4×4×13

= 32 + 208 = 240 cm²

De totale oppervlakte van het gegeven prisma is dus 240 vierkante cm.

Probleem 3: Bepaal de basislengte van een vijfhoekig prisma als de totale oppervlakte 100 vierkante eenheden bedraagt ​​en de hoogte en apothemalengte respectievelijk 8 eenheden en 5 eenheden zijn.

Oplossing:

Gezien gegevens,

De totale oppervlakte van het vijfhoekige prisma = 100 vierkante eenheden

De hoogte van het prisma (h) = 8 eenheden

Apothemlengte (a) = 5 eenheden

We weten dat,

De totale oppervlakte van het vijfhoekige prisma = 5ab + 5bh

⇒ 100 = 5b (a+ h)

⇒ 100/5 = b(5 + 8)

⇒ 20 = b × (13) ⇒ b = 25/16 = 1,54 eenheden

De basislengte is dus 1,54 eenheden

Probleem 4: Bepaal de hoogte van het rechthoekige prisma en de totale oppervlakte van een rechthoekig prisma als het laterale oppervlak 540 vierkante cm bedraagt ​​en de lengte en breedte van de basis respectievelijk 13 cm en 7 cm zijn.

Oplossing:

Gezien gegevens,

De lengte van de rechthoekige basis (l) = 13 cm

De breedte van de rechthoekige basis (b) = 7 cm

Het laterale oppervlak van het prisma = 540 vierkante cm

We hebben,

Het laterale oppervlak van het prisma = basisomtrek × hoogte

⇒ 540 = 2 (l + b) u

⇒ 2 (13 + 7) u = 540

⇒ 2 (20) h = 540 ⇒ h = 13,5 cm

wat is android easter egg

We weten dat,

De totale oppervlakte van het rechthoekige prisma = 2 (lw + wh + lh)

= 2 × (13 × 7 + 7 × (13,5) + 13 × (13,5))

= 2 × (91 + 94,5 + 175,5) = 722 vierkante cm

De hoogte en het totale oppervlak van het gegeven rechthoekige prisma bedragen dus respectievelijk 13,5 cm en 722 vierkante cm.

Probleem 5: Bepaal de oppervlakte van het reguliere zeshoekige prisma als de hoogte van het prisma 12 inch is en de lengte van de zijkant van de basis 5 inch is.

Oplossing:

Gezien gegevens,

De hoogte van het prisma (h) = 12 inch

De lengte van de zijkant van de basis (a) = 6 inch

De oppervlakte van een regelmatig zeshoekig prisma = 6ah + 3√3a²

= 6 × 5 × 12 + 3√3(5)²

= 360 + 75√3

= 360 + 75 × (1,732) = 489,9 vierkante inch

De oppervlakte van het gegeven prisma is dus 489,9 vierkante inch.

Probleem 6: Bereken de laterale en totale oppervlakte van een driehoekig prisma waarvan de basisomtrek 25 inch is, de basislengte en hoogte van de driehoek 9 inch en 10 inch zijn, en de hoogte van het prisma 14 inch is.

Oplossing:

Gezien gegevens,

De hoogte van het prisma (H) = 14 inch

De basisomtrek van het prisma (P) = 25 inch

De basislengte van de driehoek = 9 inch

De hoogte van de driehoek = 10 inch

We weten dat,

Het laterale oppervlak van het prisma = basisomtrek × hoogte

= 25 × 14= 350 vierkante meter

Oppervlakte van de driehoekige basis (A) = ½ × basis × hoogte = 1/2 × 9 × 10 = 45 vierkante inch

De totale oppervlakte van het driehoekige prisma = 2A + PH

= 2 × 45 + 25 × 14 = 90 + 350 = 440 vierkante meter

Daarom zijn de laterale en totale oppervlakten van het prisma respectievelijk 350 vierkante meter en 440 vierkante meter.

Oefenproblemen op het oppervlak van een prisma

1. Gegeven een rechthoekig prisma met afmetingen:

Vlc mediaspeler download youtube

• Lengte = 6 cm
• Breedte = 4 cm
• Hoogte = 5 cm

Bereken de totale oppervlakte.

2. Beschouw een driehoekig prisma met afmetingen:

• Basis van de driehoek = 8 cm
• Hoogte van de driehoek = 6 cm
• Lengte van het prisma = 10 cm

Bereken de totale oppervlakte.

3. Bepaal de oppervlakte van een regelmatig vijfhoekig prisma met:

• Zijlengte van de basis = 7 cm
• Hoogte van het prisma = 9 cm.

4. Bereken de oppervlakte van een zeshoekig prisma met:

• Zijlengte van de reguliere zeshoekige basis = 10 cm
• Hoogte van het prisma = 12 cm.

Oppervlakte van een prisma – Veelgestelde vragen

Wat is een prisma in de geometrie?

Een prisma is een driedimensionale vorm met twee congruente parallelle bases en rechthoekige of parallellogramzijvlakken die deze verbinden. Prisma's zijn er in verschillende vormen, zoals rechthoekige prisma's, driehoekige prisma's en vijfhoekige prisma's, elk met unieke kenmerken.

Hoe vind je het oppervlak van een prisma?

Om de oppervlakte van een prisma te vinden, berekent u de oppervlakte van alle vlakken en telt u ze vervolgens bij elkaar op. Voor een rechthoekig prisma is de oppervlakteformule 2lw + 2lh + 2wh, waarbij l de lengte is, w de breedte en h de hoogte. Voor andere typen prisma's, zoals driehoekige of vijfhoekige prisma's, kunnen aanvullende formules voor het basisoppervlak en het laterale oppervlak nodig zijn.

Wat zijn de eigenschappen van een prisma?

Prisma's hebben verschillende belangrijke eigenschappen:

• Ze hebben twee congruente parallelle bases.
• De zijvlakken zijn allemaal parallellogrammen.
• De hoogte (hoogte) is de loodrechte afstand tussen de twee bases.
• De onderstellen zijn qua vorm en maat identiek.
• De doorsnede evenwijdig aan de basissen heeft altijd dezelfde vorm en grootte als de basissen.

Wat zijn enkele praktijkvoorbeelden van prisma's?

Prisma's zijn te vinden in verschillende alledaagse voorwerpen en structuren. Voorbeelden zijn onder meer:

• Rechthoekige prisma's: gebouwen, graandozen, boeken.
• Driehoekige prisma's: Daken van huizen, wigvormige voorwerpen.
• Vijfhoekige prisma's: sommige soorten kolommen, bepaalde architecturale structuren.
• Zeshoekige prisma's: bepaalde soorten kristallen, sommige verpakkingscontainers.

Waarom is het oppervlak belangrijk bij prisma's?

Het oppervlak is cruciaal bij prisma's, omdat het de totale oppervlakte van alle oppervlakken (vlakken) van het prisma vertegenwoordigt. Het begrijpen van het oppervlak helpt bij verschillende praktische toepassingen, zoals het berekenen van de hoeveelheid materiaal die nodig is om een ​​prismavormig object te bouwen of te bedekken, het bepalen van de warmteoverdrachtssnelheid en het optimaliseren van het verpakkingsontwerp.