- DFA verwijst naar deterministische eindige automaten. Deterministisch verwijst naar het unieke karakter van de berekening. De eindige automaten worden deterministische eindige automaten genoemd als de machine symbool voor teken een invoerreeks wordt gelezen.
- In DFA is er slechts één pad voor specifieke invoer van de huidige status naar de volgende status.
- DFA accepteert de nulbeweging niet, dat wil zeggen dat de DFA de status niet kan veranderen zonder enig invoerteken.
- DFA kan meerdere eindtoestanden bevatten. Het wordt gebruikt bij lexicale analyse in Compiler.
In het volgende diagram kunnen we zien dat er vanuit toestand q0 voor invoer a slechts één pad is dat naar q1 gaat. Op dezelfde manier is er vanaf q0 slechts één pad voor invoer b die naar q2 gaat.
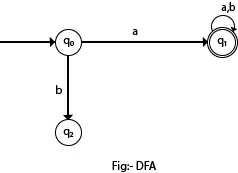
Formele definitie van DFA
Een DFA is een verzameling van 5 tupels, dezelfde als we hebben beschreven in de definitie van FA.
Q: finite set of states ∑: finite set of the input symbol q0: initial state F: final state δ: Transition function
Overgangsfunctie kan worden gedefinieerd als:
δ: Q x ∑→Q
Grafische weergave van DFA
Een DFA kan worden weergegeven door digraphs, genaamd toestandsdiagrammen. Waarin:
- De staat wordt weergegeven door hoekpunten.
- De boog die is gelabeld met een invoerteken toont de overgangen.
- De begintoestand is gemarkeerd met een pijl.
- De eindtoestand wordt aangegeven met een dubbele cirkel.
Voorbeeld 1:
Q = {q0, q1, q2} ∑ = {0, 1} q0 = {q0} F = {q2} Oplossing:
Overgangsdiagram:

Overgangstabel:
| Huidige staat | Volgende status voor ingang 0 | Volgende status van ingang 1 |
|---|---|---|
| →q0 | Q0 | q1 |
| q1 | Q2 | q1 |
| *q2 | Q2 | Q2 |
Voorbeeld 2:
DFA met ∑ = {0, 1} accepteert alles beginnend met 0.
Oplossing:

Uitleg:
- In het bovenstaande diagram kunnen we zien dat bij gegeven 0 als invoer voor DFA in status q0 de DFA van status verandert naar q1 en altijd naar de eindstatus q1 gaat bij het starten van invoer 0. Het kan 00, 01, 000, 001 accepteren... .enz. Het kan geen enkele string accepteren die begint met 1, omdat het nooit naar de eindstatus zal gaan op een string die begint met 1.
Voorbeeld 3:
DFA met ∑ = {0, 1} accepteert alles dat eindigt op 0.
Oplossing:

Uitleg:
In het bovenstaande diagram kunnen we zien dat bij gegeven 0 als invoer voor DFA in toestand q0, de DFA van toestand verandert naar q1. Het kan elke tekenreeks accepteren die eindigt op 0, zoals 00, 10, 110, 100... enz. Het kan geen enkele string accepteren die eindigt op 1, omdat het nooit naar de eindstatus q1 zal gaan bij invoer van 1, dus de string die eindigt op 1 zal niet worden geaccepteerd of zal worden afgewezen.
