Wat is een skiplijst?
Een skiplist is een probabilistische datastructuur. De skiplijst wordt gebruikt om een gesorteerde lijst met elementen of gegevens op te slaan met een gekoppelde lijst. Het maakt het mogelijk om het proces van de elementen of gegevens efficiënt te bekijken. In één enkele stap slaat het verschillende elementen van de hele lijst over. Daarom wordt het ook wel een skip-lijst genoemd.
De skiplijst is een uitgebreide versie van de gekoppelde lijst. Hiermee kan de gebruiker het element zeer snel zoeken, verwijderen en invoegen. Het bestaat uit een basislijst die een reeks elementen bevat die de linkhiërarchie van de volgende elementen handhaaft.
Lijststructuur overslaan
Het is gebouwd in twee lagen: de onderste laag en de bovenste laag.
De onderste laag van de skip-lijst is een algemeen gesorteerde gekoppelde lijst, en de bovenste lagen van de skip-lijst zijn als een 'express-regel' waar de elementen worden overgeslagen.
Complexiteitstabel van de Skip-lijst
| Ja nee | Complexiteit | Gemiddeld geval | Het slechtste geval |
|---|---|---|---|
| 1. | Toegang tot complexiteit | O(login) | Op) |
| 2. | Zoekcomplexiteit | O(login) | Op) |
| 3. | Verwijder complexiteit | O(login) | Op) |
| 4. | Voeg complexiteit toe | O(login) | Op) |
| 5. | Complexiteit van de ruimte | - | O(nlogn) |
Werking van de Skip-lijst
Laten we een voorbeeld nemen om de werking van de skiplijst te begrijpen. In dit voorbeeld hebben we 14 knooppunten, zodanig dat deze knooppunten in twee lagen zijn verdeeld, zoals weergegeven in het diagram.
De onderste laag is een gemeenschappelijke lijn die alle knooppunten met elkaar verbindt, en de bovenste laag is een uitdrukkelijke lijn die alleen de hoofdknooppunten met elkaar verbindt, zoals u in het diagram kunt zien.
Stel dat u in dit voorbeeld 47 wilt vinden. U begint met zoeken vanaf het eerste knooppunt van de expreslijn en blijft op de expreslijn lopen totdat u een knooppunt vindt dat gelijk is aan 47 of meer dan 47.
Je kunt in het voorbeeld zien dat 47 niet bestaat in de expreslijn, dus je zoekt naar een knooppunt van minder dan 47, wat 40 is. Nu ga je naar de normale lijn met behulp van 40, en zoek de 47, zoals weergegeven in het diagram.
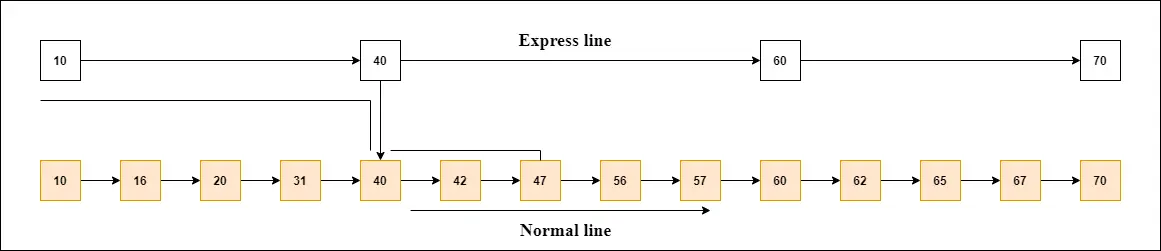
Let op: Zodra je zo'n knooppunt op de 'snellijn' hebt gevonden, ga je van dit knooppunt naar een 'normale rijstrook' met behulp van een aanwijzer en zoek je naar het knooppunt in de normale lijn.
Lijst met basishandelingen overslaan
Er zijn de volgende soorten bewerkingen in de overslaanlijst.
Algoritme van de invoegbewerking
Insertion (L, Key) local update [0...Max_Level + 1] a = L → header for i = L → level down to 0 do. while a → forward[i] → key forward[i] update[i] = a a = a → forward[0] lvl = random_Level() if lvl > L → level then for i = L → level + 1 to lvl do update[i] = L → header L → level = lvl a = makeNode(lvl, Key, value) for i = 0 to level do a → forward[i] = update[i] → forward[i] update[i] → forward[i] = a
Algoritme van verwijderingsbewerking
Deletion (L, Key) local update [0... Max_Level + 1] a = L → header for i = L → level down to 0 do. while a → forward[i] → key forward[i] update[i] = a a = a → forward[0] if a → key = Key then for i = 0 to L → level do if update[i] → forward[i] ? a then break update[i] → forward[i] = a → forward[i] free(a) while L → level > 0 and L → header → forward[L → level] = NIL do L → level = L → level - 1
Algoritme van zoekbewerking
Searching (L, SKey) a = L → header loop invariant: a → key level down to 0 do. while a → forward[i] → key forward[i] a = a → forward[0] if a → key = SKey then return a → value else return failure
Voorbeeld 1: Maak een skip-lijst, we willen deze volgende sleutels in de lege skip-lijst invoegen.
- 6 met niveau 1.
- 29 met niveau 1.
- 22 met niveau 4.
- 9 met niveau 3.
- 17 met niveau 1.
- 4 met niveau 2.
Jaren:
Stap 1: Plaats 6 met niveau 1

Stap 2: Vul 29 in met niveau 1

Stap 3: Vul 22 in met niveau 4

Stap 4: Plaats 9 met niveau 3

Stap 5: Vul 17 in met niveau 1

Stap 6: Plaats 4 met niveau 2

Voorbeeld 2: Beschouw dit voorbeeld waarin we naar sleutel 17 willen zoeken.

Jaren:

Voordelen van de Skip-lijst
- Als u een nieuw knooppunt in de skiplijst wilt invoegen, zal het knooppunt zeer snel worden ingevoegd omdat er geen rotaties in de skiplijst voorkomen.
- De skiplist is eenvoudig te implementeren in vergelijking met de hashtabel en de binaire zoekboom.
- Het is heel eenvoudig om een knooppunt in de lijst te vinden, omdat de knooppunten in gesorteerde vorm worden opgeslagen.
- Het skiplist-algoritme kan heel eenvoudig worden gewijzigd in een meer specifieke structuur, zoals indexeerbare skip-lijsten, bomen of prioriteitswachtrijen.
- De overslaanlijst is een robuuste en betrouwbare lijst.
Nadelen van de Skip-lijst
- Het vereist meer geheugen dan de gebalanceerde boom.
- Omgekeerd zoeken is niet toegestaan.
- De skiplijst doorzoekt het knooppunt veel langzamer dan de gekoppelde lijst.
Toepassingen van de Skip-lijst
- Het wordt gebruikt in gedistribueerde applicaties en vertegenwoordigt de pointers en het systeem in de gedistribueerde applicaties.
- Het wordt gebruikt om een dynamische, elastische gelijktijdige wachtrij met weinig vergrendelingsconflicten te implementeren.
- Het wordt ook gebruikt met de QMap-sjabloonklasse.
- De indexering van de skiplijst wordt gebruikt bij het uitvoeren van mediaanproblemen.
- De skiplijst wordt gebruikt voor het posten van delta-codering in de Lucene-zoekopdracht.
