Kwadrant wordt gedefinieerd als een gebied in de ruimte dat in vier gelijke delen is verdeeld door twee assen, namelijk de X-as en de Y-as in het cartesiaanse vlak. Deze twee assen snijden elkaar onder een hoek van 90 graden en de vier aldus gevormde gebieden worden vier kwadranten genoemd, namelijk I kwadrant, II kwadrant, III kwadrant en IV kwadrant.
Linux-bestanden
In dit artikel zullen we essentiële kwadrantconcepten onderzoeken, waaronder wat een kwadrant is, de oppervlakte, de kwadrantgrafiek, het cartesiaanse vlak, tekenconventies binnen het kwadrant, de abscis en de coördinaat, evenals het uitzetten van punten op een kwadrant.
Inhoudsopgave
- Wat zijn kwadranten van een grafiek?
- Onderteken de Conventie in Kwadranten
- Punten in kwadranten uitzetten
- Trigonometrische waarden in verschillende kwadranten
Wat zijn kwadranten van een grafiek?
Een kwadrant is een aangewezen gebied op a Cartesisch vlak , gecreëerd door de kruising van de X- en Y-assen. In dit vlak worden vier kwadranten gevormd, elk met zijn unieke eigenschappen. Het eerste kwadrant, rechtsboven, heeft positieve x- en y-coördinaten. Het tweede kwadrant, linksboven, heeft negatieve x- en positieve y-coördinaten, enzovoort. Het begrijpen van deze kwadranten is essentieel voor het lokaliseren en interpreteren van punten in de grafiek, waardoor een systematische manier wordt geboden om Cartesiaanse coördinaten te navigeren en te analyseren.
4 kwadranten op coördinatenvlak
Het cartesiaanse vlak, gevormd door de X- en Y-assen, is opgesplitst in vier kwadranten, elk met verschillende kenmerken:
- Eerste kwadrant: Rechtsboven zijn zowel de x- als de y-coördinaten positief. Dit kwadrant vertegenwoordigt punten in het rechterbovengedeelte van het vlak.
- Tweede kwadrant: Gelegen linksboven is de x-coördinaat negatief en de y-coördinaat positief. Dit kwadrant omvat punten in het linkerbovengedeelte van het vlak.
- Derde kwadrant: Linksonder gepositioneerd, zijn zowel de x- als de y-coördinaten negatief. Punten in het gebied linksonder in het vlak vallen in dit kwadrant.
- Vierde kwadrant: Rechtsonder is de x-coördinaat positief en de y-coördinaat negatief. Dit kwadrant omvat punten in het gedeelte rechtsonder van het vlak.
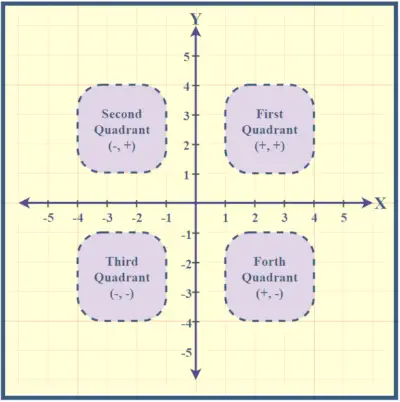
De kwadranten zijn tegen de klok in genummerd, beginnend vanaf rechtsboven. Het punt waar de X- en Y-assen elkaar kruisen, wordt de oorsprong genoemd, met coördinaten (0,0), die nulwaarden aangeven voor zowel x als y. Het begrijpen van deze kwadranten helpt bij het lokaliseren van punten binnen het cartesiaanse vlak.
Wat is oorsprong?
Het startpunt van een grafiek, ook wel de oorsprong genoemd en weergegeven als (0, 0), is het punt waar de horizontale x-as en de verticale y-as elkaar kruisen. Dit betekent dat bij de oorsprong de waarden voor zowel x als y nul zijn. Het dient als referentiepunt voor het lokaliseren van andere punten in de grafiek. In de hierboven toegevoegde afbeelding toont punt O de oorsprong.
Abcis en ordinaat in kwadranten
In de vier kwadranten worden getallen weergegeven als paren (a, b), waarbij ‘a’ staat voor de x-coördinaat en ‘b’ voor de y-coördinaat. Om erachter te komen waar een punt ligt zonder te plotten, let je op de tekens van de x-coördinaat (abscis) en y-coördinaat (coördinaat). Als u bijvoorbeeld een punt als Q (3, -5) heeft, geven de tekens (+ve, -ve) aan dat dit in kwadrant IV ligt.
De abscis toont de horizontale afstand tot de Y-as. Een positieve abscis betekent naar rechts, en in ons voorbeeld betekent abscis = 3 dat je vanaf de oorsprong langs de x-as 3 eenheden naar rechts gaat.
De ordinaat geeft de verticale afstand tot de oorsprong aan. Een negatieve ordinaat betekent dat je vanaf de oorsprong langs de y-as naar beneden gaat. In het voorbeeld betekent ordinaat = -5: een daling met 5 eenheden.
Onderteken de Conventie in Kwadranten
Tekenconventies in de kwadranten kunnen gemakkelijk worden begrepen met behulp van de onderstaande afbeelding,

In het XY-vlak neemt de x-coördinaat toe als we van links naar rechts langs de x-as bewegen. Op dezelfde manier resulteert het bewegen van onder naar boven langs de y-as in een toename van de y-coördinaat. Het XY-vlak is verdeeld in vier kwadranten, elk met specifieke tekenconventies voor x- en y-coördinaten:
| Kwadrant | x-coördinaat | y-coördinaat |
|---|---|---|
| 1e Kwadrant | Positief (+) | Positief (+) |
| 2e kwadrant | Negatief (-) | Positief (+) |
| 3e kwadrant | Negatief (-) | Negatief (-) |
| 4e kwadrant | Positief (+) | Negatief (-) |
Daarom hebben punten in het eerste kwadrant positieve waarden voor zowel x als y, die in het tweede kwadrant hebben een negatieve x en een positieve y, het derde kwadrant heeft zowel negatieve x- als y-waarden, en het vierde kwadrant heeft een positieve x en een negatieve y.
Punten in kwadranten uitzetten
In een cartesiaans vlak worden punten geïdentificeerd door de x-as en y-as. Deze punten worden aangegeven als (a, b), waarbij ‘a’ de x-coördinaat (abscis) is, en ‘b’ de y-coördinaat (ordinaat). Om een punt in een kwadrant te positioneren, beschouwen we de tekens van deze coördinaten. De waarden van x en y geven aan hoe ver het punt zich respectievelijk van de x-as en de y-as bevindt.
Teken bijvoorbeeld het punt (2, -5) op het cartesische vlak. Uit analyse van het teken van de coördinaten blijkt dat het punt zich in het 4e kwadrant bevindt. Het zal 2 eenheden verwijderd zijn van de x-as (naar rechts) en 5 eenheden verwijderd van de y-as (naar beneden), waarbij de oorsprong als referentiepunt wordt gebruikt.
Trigonometrische waarden in verschillende kwadranten
De waarden van verschillende trigonometrische functies in verschillende kwadranten kan worden geleerd door de onderstaande tabel te bestuderen als:
| Kwadrant | Zonder java-waarde van enum | Cos | Dus | Cosecant | Secans | Cotangens |
|---|---|---|---|---|---|---|
| 1e Kwadrant | + | + | + | + | + | + |
| 2e kwadrant | + | – | + | + | – | – |
| 3e kwadrant | – | – | – | – | – | + |
| 4e kwadrant | – | – | – | – | + | – |
In het eerste kwadrant zijn alle trigonometrische verhoudingen positief. In het tweede kwadrant zijn Sinus en Cosecant positief (+), terwijl Cosinus en Secant negatief zijn (-). In het derde kwadrant zijn Tangens en Cotangens positief (+), terwijl Cosinus en Secans negatief zijn (-). In het 4e kwadrant zijn Sinus en Cosecant negatief (-), terwijl Cosinus en Secant positief zijn (+).
Lees verder,
- Coördineer geometrie
- Parallelle lijnen
- Afstandsformule
Opgeloste voorbeelden in het kwadrant
Voorbeeld 1: Teken punt A (3, -4) en identificeer het kwadrant ervan.
Oplossing:
Punt A bevindt zich op de coördinaten (3, -4). Omdat de x-coördinaat positief is (3) en de y-coördinaat negatief (-4), ligt punt A in kwadrant IV.
Voorbeeld 2: Teken het punt P (-5, 2) en bepaal het kwadrant ervan
Oplossing:
De coördinaten van punt P zijn (-5, 2). Om het kwadrant te bepalen, onderzoeken we de tekens van de x- en y-coördinaten.
De X-coördinaat is -5, wat een positie links van de oorsprong aangeeft.
De Y-coördinaat is 2, wat een positie boven de oorsprong aangeeft.
Omdat de x-coördinaat negatief is en de y-coördinaat positief, bevindt punt P zich daarom in Kwadrant II.
Punt P (-5, 2) bevindt zich in kwadrant II van het cartesiaanse vlak.
Oefen problemen op kwadranten
Probleem 1: Teken het punt (1, -1) en identificeer het kwadrant ervan.
Probleem 2: Zoek drie punten op de x-as en bepaal hun kwadranten.
Probleem 3: Als een punt op de y-as ligt met coördinaten (0, -3), in welk kwadrant bevindt het zich dan?
Probleem 4: Lokaliseer de punten Q (2, 2), R (-2, -2) en S (0, 0) en controleer op collineariteit.
Probleem 5: Teken het punt (-4, -3) en leg uit in welk kwadrant het ligt.
arraylist sorteren
Veelgestelde vragen over kwadranten
1. Wat is een kwadrant in wiskunde?
In de wiskunde is een kwadrant een van de vier secties die ontstaan door het snijpunt van twee loodrechte lijnen of assen. Deze assen worden doorgaans aangeduid als de x-as en y-as in een cartesiaans coördinatensysteem.
2. Hoe wordt het snijpunt van twee assen genoemd?
Het snijpunt van twee assen in een cartesiaans coördinatensysteem wordt de oorsprong genoemd. Het wordt weergegeven door het punt waar de x-as en de y-as samenkomen, meestal aangegeven als (0,0).
3. Wat zijn 4 kwadranten?
De vier kwadranten zijn de secties die worden gevormd door een cartesiaans coördinatenvlak in vier gelijke delen te verdelen. Ze worden aangeduid als het eerste kwadrant (Q1), het tweede kwadrant (Q2), het derde kwadrant (Q3) en het vierde kwadrant (Q4).
4. Welk kwadrant is positief?
Het positieve kwadrant in een cartesiaans coördinatensysteem is het eerste kwadrant (Q1). In dit kwadrant zijn zowel de x- als de y-coördinaten positief.
5. Wat is het gebruik van kwadranten in grafieken?
Kwadranten in grafieken bieden een systematische manier om punten te ordenen en te lokaliseren op basis van hun coördinaten. Ze helpen bij het visualiseren van relaties tussen variabelen en het analyseren van patronen in datasets, waardoor het gemakkelijker wordt om grafische representaties te interpreteren.
6. Welk kwadrant heeft beide waarden van Coördinaten Positief?
Het eerste kwadrant (Q1) is het kwadrant waarin zowel de x- als de y-coördinaten van punten positief zijn. Het is het enige kwadrant met beide positieve waarden.
7. Wat zijn de vier kwadranten van een cirkel?
Het concept van kwadranten is niet rechtstreeks van toepassing op cirkels. In plaats daarvan worden cirkels verdeeld in hoeken, gemeten in graden. Als je echter naar circulaire sectoren verwijst, zou je termen kunnen gebruiken als eerste sector, tweede sector, derde sector en vierde sector, die overeenkomen met verschillende hoekgebieden.
