De afkoelingswet van Newton is de fundamentele wet die de snelheid beschrijft van de warmteoverdracht door een lichaam naar zijn omgeving door middel van straling. Deze wet stelt dat de snelheid waarmee het lichaam warmte uitstraalt recht evenredig is met het temperatuurverschil tussen het lichaam en de omgeving, gegeven het feit dat het temperatuurverschil klein is. dat wil zeggen: hoe groter het verschil tussen de temperatuur van het lichaam en de omgeving, hoe meer warmte verloren gaat en hoe lager de temperatuur, hoe minder warmte verloren gaat. De afkoelingswet van Newton is een speciaal geval van de wet van Stefan-Boltzmann.

In dit artikel zullen we in detail leren over Newton's Law of Cooling, Newton's Law of Cooling Formula, de afleiding ervan, voorbeelden en andere.

Definitie van de afkoelingswet van Newton

Newton was de eerste die de relatie bestudeerde tussen de warmte die een lichaam verliest aan zijn omgeving. Hij stelt dat hoe meer temperatuurverschil tussen het object en de omgeving, hoe meer warmte het lichaam uitstraalt.

Newtons wet van koeling zegt dat

De snelheid waarmee een lichaam warmte verliest, is recht evenredig met het temperatuurverschil tussen het lichaam en zijn omgeving, aangezien het temperatuurverschil niet groot is.

Deze wet wordt gebruikt om uit te leggen waarom heet water of melk die op tafel blijft staan ​​sneller afkoelt dan een beetje warme melk of water dat op tafel blijft staan. De afkoelingswet van Newton helpt ons de temperatuur van iemand te meten zonder deze daadwerkelijk te meten, gegeven de begintemperatuur van het lichaam en de temperatuur van de omgeving.

Newton's wet van koelformule

Newton’s Law of Cooling Formula is een formule voor het berekenen van de temperatuur van een materiaal wanneer het door straling warmte verliest aan de omgeving.

Volgens de afkoelingswet van Newton geldt:

De snelheid van warmteverlies ( – dQ/dt) van het lichaam is recht evenredig met het temperatuurverschil [ΔT = (T ₂ - T ₁ )] van het lichaam en de omgeving.

welke maanden bevinden zich in q3

We kunnen het voorstellen als,

– dQ/dt ∝ (T ₂ - T ₁ )

– dQ/dt = k(T ₂ - T ₁ )

waar,
k is een evenredigheidsconstante

Als we de bovenstaande differentiaalvergelijking oplossen, krijgen we:

T(t) = T _S + (T _O - T _S ) Het is ^-kt

waar,
T is de tijd
T(t) is de temperatuur van het lichaam op tijdstip t
T _S is de omgevingstemperatuur
T _O is de begintemperatuur van het lichaam
k is de evenredigheidsconstante

Afleiding van de afkoelingswet van Newton

De formule van de afkoelingswet van Newton kan worden afgeleid met behulp van de oplossing van de differentiaalvergelijking. Stel dat een lichaam met massa m en een specifieke warmtecapaciteit s een temperatuur T heeft₂en T₁is de temperatuur van de omgeving.

Als de temperatuur een klein beetje daalt dT ₂ op tijd dt , dan is de hoeveelheid verloren warmte:

dQ = ms dT ₂

De snelheid van warmteverlies wordt gegeven door,

dQ/dt = ms (dT ₂ /dt)

Volgens de afkoelingswet van Newton geldt:

– dQ/dt = k(T ₂ - T ₁ )

Vergelijking van de bovenstaande vergelijking

– ms (dT ₂ /dt) = k (T ₂ - T ₁ )

bekijk cartoononline.io-alternatieven

dT ₂ /(T ₂ -T ₁ ) = – (k / ms) dt

dT ₂ /(T ₂ - T ₁ ) = – Kdt

waar, K = k/m·s

Integratie van de bovenstaande vergelijking

loggen _{Het is} (T ₂ - T ₁ ) = – Kt + c

T ₂ = T ₁ + C’ en ^–Kt

waar, C’ = e ^C

De relatie tussen de temperatuurdaling van het lichaam en de tijd wordt weergegeven met behulp van de afkoelingsgrafiek. De helling van deze grafiek toont de snelheid waarmee de temperatuur daalt.

De afkoelingscurve is een grafiek die de relatie tussen lichaamstemperatuur en tijd laat zien. De snelheid waarmee de temperatuur daalt, wordt op elk punt bepaald door de helling van de raaklijn aan de curve. De onderstaande afbeelding toont de relatie tussen temperatuurdaling en tijd.

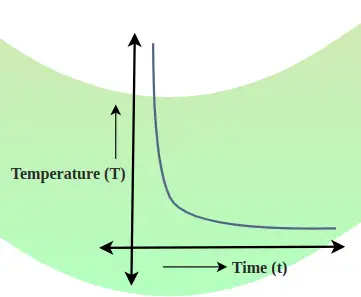
In het algemeen,

T(t) = T _A +(T _H -T _A )Het is ^-kt

waar
T(t) is de temperatuur op tijdstip t
T _A is de omgevingstemperatuur of temperatuur van de omgeving
T _H is de temperatuur van het hete object
k is de positieve constante en t is de tijd

Methoden om de afkoelingswet van Newton toe te passen

Bij een constante afkoelingssnelheid is de afkoelingssnelheid gerelateerd aan de gemiddelde temperatuur van het lichaam gedurende het interval. Vervolgens kunnen we de geschatte waarde berekenen met behulp van de wet van Newton op het gebied van koeling.

dθ/dt = k(q – q _S )

waar,
Q is de lichaamstemperatuur
Q _S is de temperatuur van de omgeving

Als de gemiddelde temperatuur van het lichaam nu q is, waar,

q = (q _i + q _F )/2

Verificatie van de afkoelingswet van Newton

We kunnen de afkoelingswet van Newton eenvoudig verifiëren met het hieronder beschreven experiment:

In het experiment nemen we een dubbelwandig vat (V) met water tussen de twee wanden. In het dubbelwandige vat nemen we een koperen calorimeter (C) met heet water.

We gebruiken twee thermometers T₂om de temperatuur van het water in de calorimeter en T te meten₁om de temperatuur te meten van het warme water tussen de dubbele wanden. Na gelijke tijdsintervallen worden beide temperaturen genoteerd en een grafiek tussen de log_{Het is}(T₂-T₁) en tijd (t) wordt uitgezet, die verschijnt als een rechte lijn met een negatieve helling.

Newton's wet van afkoelingsgrafiek

De grafiek van de afkoelingswet van Newton is hieronder toegevoegd, in deze grafiek wordt het logaritmische verschil tussen de twee temperaturen en de tijd weergegeven.

Beperkingen van de afkoelingswet van Newton

Verschillende beperkingen van de wet van koeling van Newton zijn:

• De afkoelingswet van Newton geldt als het temperatuurverschil tussen het lichaam en de omgeving klein is.
• Het warmteverlies door het lichaam vindt alleen plaats in de vorm van warmte Straling .
• De temperatuur van de omgeving moet constant blijven tijdens het afkoelen van het lichaam, anders geldt de wet van Newton van afkoeling niet.

Toepassingen van de afkoelingswet van Newton

Verschillende toepassingen van de wet van koeling van Newton zijn:

• Om in te schatten hoe lang het duurt voordat een warm object is afgekoeld tot een bepaalde temperatuur.
• Om de temperatuur van een drankje in de koelkast te bepalen nadat een bepaalde tijdsduur is verstreken.
• Het helpt om het tijdstip van overlijden aan te geven door te kijken naar de mogelijke lichaamstemperatuur op het moment van overlijden en de huidige lichaamstemperatuur.

Lees verder,

• Specifieke warmte capaciteit
• Basisconcept van de thermodynamica
• Thermodynamische processen

Opgeloste voorbeelden Newtons wet van koeling

Voorbeeld 1: Een pan gevuld met warm voedsel koelt in 2 minuten af ​​van 94 °C naar 86 °C als de kamertemperatuur 20 °C bedraagt. Hoe lang duurt het om af te koelen van 71 °C naar 69 °C?

Oplossing:

Gemiddeld 94 °C en 86 °C is 90 °C,

• T₂= 90°C
• T₁= 20°C

Drop-in-temp. van voedsel is 8 °C in 2 minuten.

Volgens de afkoelingswet van Newton geldt:

– dQ/dt = k(T ₂ -T ₁ )

8 °C /2 min = k(90 – 20)

4 = k(70) ………(1)

afwaardering onderstrepen

Gemiddeld is 69 °C en 71 °C 70 °C

• T₂= 70°C
• T₁= 20°C

Volgens de afkoelingswet van Newton geldt:

2 °C /dt = k(70 – 20) ……(2)

Uit vergelijking (1) en (2),

Verandering in tijd = 0,7 min = = 42 sec

Het voedsel heeft dus 42 seconden nodig om af te koelen van 71 °C naar 69 °C.

Voorbeeld 2: Een lichaam met een temperatuur van 40ºC wordt in een omgeving met een constante temperatuur van 20ºC gehouden. Er wordt waargenomen dat de temperatuur in 10 minuten daalt tot 35ºC. Bereken hoeveel tijd het lichaam nodig heeft om een ​​temperatuur van 30ºC te bereiken.

Oplossing:

Gegeven,

• Q_i= (40 – 20)ºC
• Q_F= (35 – 20)ºC

Volgens de afkoelingswet van Newton

Q _F = q _i Het is ^-kt

Nu, voor het interval waarin de temperatuur daalt van 40 ºC naar 35 ºC.

(35 – 20) = (40 – 20) en^-(10k)

Het is^-10k= 3/4

-10k = (ln 4/3)

k = 0,2876/10

k = 0,02876

Gebruik nu opnieuw de formule van Newon:

(30 – 20) = (35 – 20)e^-kt

10 = 15e^-kt

Het is^-kt= 23

-kt = ln(2/3)

t = 0,40546/k

rand met css

Gebruikmakend van de waarde van de k,

t = 0,40546/0,02876

t = 14,098 min

De tijd die het lichaam nodig heeft om de temperatuur van 30ºC te bereiken bedraagt ​​dus 14,098 minuten

Voorbeeld 3: De olie wordt verwarmd tot 70 ºC. Na 6 minuten koelt het af tot 50 ºC. Bereken de tijd die de olie nodig heeft om af te koelen van 50 ºC naar 40 ºC, gegeven de omgevingstemperatuur T _S = 25ºC

Oplossing:

Gegeven,

Temperatuur van de olie na 6 minuten, d.w.z. T(t) is gelijk aan 50 ºC

• Omgevingstemperatuur T_S= 25ºC
• Temperatuur van olie, T_O= 70ºC
• Tijd om af te koelen tot 50ºC = 6 minuten

Volgens de afkoelingswet van Newton geldt:

T(t) = T_S+ (T₀- T_S) Het is^-kt

{T(t) – T_S}/(T_O- T_S) = en^-kt

-kt = ln[(T(t) – T_S)/(T_O- T_S)] ………(1)

Vervang de waarden

-kt = ln[(50 – 25)/(70 – 25)]

-k = (ln 0,55556)/6

k = 0,09796

De gemiddelde temperatuur van 50 ºC tot 40 ºC is gelijk aan 45 ºC

Opnieuw gebruik makend van de afkoelingswet van Newton

-(0,09796)t = ln[(45 – 25)/(70 – 25)]

knop om css te centreren

-0,09796t = ln(0,44444)

0,09796t = 0,81093

t = 0,09796/0,58778 = 8.278 min

Dit betekent dat de tijd die olie nodig heeft om af te koelen van 50 ºC naar 40 ºC gelijk is 8.278 min

Voorbeeld 4: Water wordt gedurende 10 minuten verwarmd tot 80 ºC. Hoeveel zou de temperatuur in graden Celsius zijn, als k = 0,056 per minuut en de omgevingstemperatuur 25 ºC is?

Oplossing:

Gegeven,

• Omgevingstemperatuur T_S= 25ºC
• Watertemperatuur T₀= 80ºC
• Tijd waarvoor water wordt verwarmd (t) = 10 min
• Waarde van constante k = 0,056.

Volgens de afkoelingswet van Newton geldt:

T(t) = T_S+ (T₀- T_S) Het is^-kt

De waarde vervangen

T(t)= 25 + (80 – 25)e^-(0,056×10)

T(t) = 25 + 55 e^-(0,056×10)

T(t) = 25 + 31,42

T(t) = 56,42

Na 10 minuten zou de temperatuur van het water zijn 56,42ºC.

Veelgestelde vragen over de afkoelingswet van Newton

Vraag 1: Wat is de afkoelingswet van Newton?

Antwoord:

De wet van Newton over koeling stelt dat de snelheid van warmteverlies door een lichaam recht evenredig is met het temperatuurverschil tussen het lichaam en zijn omgeving.

Vraag 2: Wat is de koelwet van Newton?

Antwoord:

De Newton’s Law of Cooling-formule stelt dat:

T(t) = T _S + (T _O - T _S ) Het is ^-kt

Vraag 3: Wat is k in de afkoelingswet van Newton?

Antwoord:

De k in de formule van Newton’s Law of Cooling is de constante die afhangt van het materiaal, d.w.z. het veranderen van het materiaal verandert de k in de wet van koeling van Newton.

Vraag 4: Waarom is warme melk gemakkelijker uit een kom te drinken dan uit een glas?

Antwoord:

Kom heeft een groter oppervlak dan glas, waardoor er meer warmte verloren gaat aan de omgeving in de vorm van warmtestraling door de kom, waardoor het voor ons gemakkelijker is om warme melk uit de kom te drinken.