Traagheidsmoment is de eigenschap van een lichaam in roterende beweging. Traagheidsmoment is de eigenschap van de roterende lichamen die de neiging hebben de verandering in de rotatiebeweging van het lichaam tegen te werken. Het is vergelijkbaar met de traagheid van elk lichaam in translatiebeweging. Wiskundig gezien wordt het traagheidsmoment gegeven als de som van het product van de massa van elk deeltje en het kwadraat van de afstand tot de rotatie-as. Het wordt gemeten in de eenheid van kgm 2 .
Laten we in het onderstaande artikel in detail meer leren over het traagheidsmoment.
Inhoudsopgave
- Definitie van traagheidsmoment
- Formule van traagheidsmoment
- Factoren die het traagheidsmoment beïnvloeden
- Hoe het traagheidsmoment berekenen?
- Moment van traagheidsformule voor verschillende vormen
- Traagheidsstraal
- Traagheidsmomentstellingen
- Traagheidsmomenten voor verschillende objecten
Definitie van traagheidsmoment
Traagheidsmoment is de neiging van een lichaam in roterende beweging dat de verandering daarin tegenwerkt roterende beweging als gevolg van externe krachten. Het traagheidsmoment gedraagt zich als hoekmassa en wordt rotatietraagheid genoemd. Traagheidsmoment is analoog aan het mechanische Luiheid van het lichaam.
MOI wordt gedefinieerd als de hoeveelheid uitgedrukt door de som van het product van de massa van elk deeltje met het kwadraat van zijn afstand tot de rotatie-as voor elk deeltje dat de rotatiebeweging uitvoert.
Eenheid van traagheidsmoment
Traagheidsmoment is een scalaire grootheid en de SI-eenheid van het traagheidsmoment is kgm 2 .
Dimensionale formule van traagheidsmoment
Omdat het traagheidsmoment wordt gegeven als het product van massa en kwadraat van afstand. Zijn dimensionale formule wordt gegeven door het product van de maatformule van massa en het kwadraat van de maatformule van lengte. De dimensionale formule van het traagheidsmoment is: ml 2
Wat is traagheid?
Traagheid is de eigenschap van een materie waardoor deze de neiging heeft weerstand te bieden aan de verandering in de toestand van zijn beweging. Dit betekent dat een lichaam in rust probeert in rust te blijven en weerstand te bieden aan elke kracht die het in beweging probeert te brengen, en een lichaam in beweging probeert in beweging te blijven en weerstand te bieden aan elke kracht die probeert de omvang van zijn beweging te veranderen. In termen van kwantiteit is het gelijk aan de maximale kracht die probeert zijn toestand te veranderen beweging .
Leer meer over Luiheid .
Formule van traagheidsmoment
Het traagheidsmoment is a scalaire kwantiteit . Wiskundig gezien wordt het product van het kwadraat van de massa van een deeltje en de afstand tot de rotatie-as het traagheidsmoment van het deeltje rond de rotatie-as genoemd.
De algemene formule voor het vinden van het traagheidsmoment van elk object is:
ik = dhr 2
waar,
M is de massa van het object’
R is de afstand vanaf de rotatie-as
Voor een lichaam dat uit continue oneindig kleine deeltjes bestaat, wordt de integrale vorm van het traagheidsmoment gebruikt om het traagheidsmoment te berekenen.
ik = ∫dI
ik =
int_{0}^{M} r^2 dm
Traagheidsmoment van een systeem van deeltjes
Traagheidsmoment van een systeem van deeltjes wordt gegeven door de formule:
ik = ∑m i R i 2
waar,
R i is de loodrechte afstand van de iedeeltje uit de as
M i is de massa van iedeeltje
De bovenstaande traagheidsmomentvergelijking vertelt dat het traagheidsmoment voor een systeem van deeltjes gelijk is aan de som van het product van de massa van elk deeltje en het kwadraat van de afstand tot de rotatieas van elk deeltje.
Voor de onderstaande figuur geldt
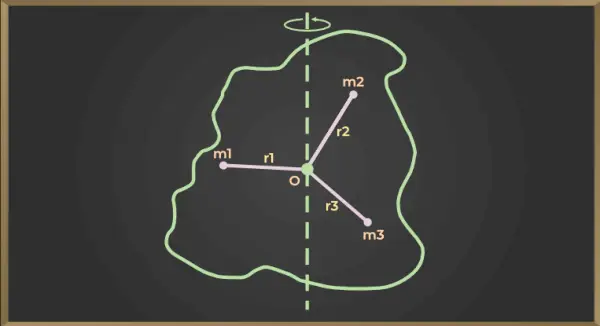
Traagheidsmoment van het eerste deeltje = m1×r12
Traagheidsmoment van tweede deeltje = m2×r22
Traagheidsmoment van derde deeltje = m3×r32
Op dezelfde manier,
Traagheidsmoment van nedeeltje = mN×rN2
Nu het traagheidsmoment van het hele lichaam rond de rotatie-as AB zal gelijk zijn aan de som van het traagheidsmoment van alle deeltjes, dus
ik = m1×r12+ m2×r22+ m3×r32+……+mN×rN2
controleer op nul in Java
ik = Σm i ×r i 2
waar,
I vertegenwoordigen het traagheidsmoment van het lichaam rond de rotatie-as
M i is de massa van iedeeltje,
R i is de straal van iedeeltje
S vertegenwoordigt de som.
Uit de vergelijking kunnen we zeggen dat het traagheidsmoment van een lichaam rond een vaste as gelijk is aan de som van het product van de massa van elk deeltje van dat lichaam en het kwadraat van zijn loodrechte afstand tot de vaste as.
Factoren die het traagheidsmoment beïnvloeden
Het traagheidsmoment van elk object is afhankelijk van de volgende waarden:
- Vorm en grootte van het object
- Dichtheid van het materiaal van het object
- As van rotatie
Hoe het traagheidsmoment berekenen?
Er zijn verschillende manieren gewend bereken het traagheidsmoment van enig roterend object.
- Voor uniforme objecten wordt het traagheidsmoment berekend door het product van de massa te nemen met het kwadraat van de afstand tot de rotatie-as (r2).
- Voor niet-uniforme objecten berekenen we het traagheidsmoment door de som te nemen van het product van individuele puntmassa's bij elke verschillende straal. Hiervoor is de gebruikte formule
ik = ∑m i R i 2
Moment van traagheidsformule voor verschillende vormen
Deze tabel bespreekt uitdrukkingen voor het traagheidsmoment voor sommige symmetrische objecten samen met hun rotatie-as:

| Voorwerp | As | Uitdrukking van het traagheidsmoment |
|---|---|---|
| Holle Cilinder Dunwandig | Centraal | ik = Dhr2 |
| Dunne ring | Diameter | ik = 1/2 heer2 |
| Ringvormige ring of holle cilinder | Centraal | ik = 1/2 M(r22+ r12) |
| Stevige cilinder | Centraal | ik = 1/2 heer2 |
| Uniforme schijf | Diameter | Ik = 1/4 Dhr2 |
| Holle bol | Centraal | Ik = 2/3 Dhr2 |
| Stevige bol | Centraal | I = 2/5 Dhr2 |
| Uniforme symmetrische bolvormige schaal | Centraal | |
| Uniforme plaat of rechthoekig parallellepipedum | Centraal | ik = 1/12 M(een2+ b2) |
| Dunne staaf | Centraal | Ik = 1/12 Dhr2 |
| Dunne staaf | Aan het einde van Rod | Ik = 1/3 Dhr2 |
Traagheidsstraal
De Traagheidsstraal van een lichaam wordt gedefinieerd als de loodrechte afstand van de rotatie-as tot het massapunt waarvan de massa gelijk is aan de massa van het hele lichaam en het traagheidsmoment gelijk is aan het werkelijke traagheidsmoment van het object zoals het is geweest aangenomen dat de totale massa van het lichaam daar geconcentreerd is. Het is een denkbeeldige afstand. De straal van de draaiing wordt aangegeven met K.
Als de massa en de draaistraal van het lichaam respectievelijk M en K zijn, dan is het traagheidsmoment van een lichaam
ik = MK 2 ……(1)
De draaiingsstraal van een lichaam staat dus loodrecht op de rotatie-as waarvan het kwadraat, vermenigvuldigd met de massa van dat lichaam, het traagheidsmoment van dat lichaam rond die as oplevert.
Opnieuw volgens vergelijking (1), K2= IK/M
K = √(I/m)
De straal van de draaiing van een lichaam om een as is dus gelijk aan de vierkantswortel van de verhouding van het lichaam om die as.
Traagheidsmomentstellingen
Er zijn twee soorten stellingen die erg belangrijk zijn met betrekking tot het traagheidsmoment:
- Stelling van de parallelle as
- Stelling van de loodrechte as
Stelling van de loodrechte as
Stelling van de loodrechte as stelt dat de som van het traagheidsmoment van een lichaam om twee onderling loodrechte assen gelegen in het vlak van een lichaam gelijk is aan het traagheidsmoment van het lichaam om de derde as die loodrecht staat op de twee assen en door hun punt gaat van kruispunt.

In de bovenstaande figuur is OS En LTD zijn twee assen in het vlak van het lichaam die loodrecht op elkaar staan. De derde as is OZ die loodrecht staat op het vlak van het lichaam en door het snijpunt van de OS En LTD bijlen. Als I X , I En , En I Met zijn de traagheidsmomenten van het lichaam rond de as OS , LTD , En OZ assen respectievelijk, dan volgens deze stelling
I X + ik En = ik Met
Stelling van de parallelle as
Volgens Parallelle as-stelling , het traagheidsmoment van een lichaam rond een gegeven as is de som van het traagheidsmoment rond een as die door het massamiddelpunt van dat lichaam gaat en het product van het kwadraat van de massa van het lichaam en de loodrechte afstand tussen de twee assen.

Laten we in de bovenstaande figuur het traagheidsmoment vinden van I O van het lichaam dat door het punt gaat O en om de as loodrecht op het vlak, terwijl het traagheidsmoment van het lichaam door het massamiddelpunt gaat C en om een as evenwijdig aan de gegeven as is I C , dan volgens deze stelling
I O = ik C + ml 2
waar
M is de massa van het hele lichaam
l is de loodrechte afstand tussen twee assen.
Traagheidsmomenten voor verschillende objecten
Traagheidsmoment van verschillende objecten wordt hieronder in dit artikel besproken
Traagheidsmoment van een rechthoekige plaat
Als de massa van de plaat M, lengte l en breedte b is, gaat het traagheidsmoment door het zwaartepunt en rond een as loodrecht op het vlak van de plaat.

ik = M(l 2 + b 2 / 12)
Traagheidsmoment van een schijf
Als de schijf een massa M en straal r heeft, dan is het traagheidsmoment rond de geometrische as van de schijf gelijk

I = 1/2(Mr 2 )
Traagheidsmoment van een staaf
Als de massa van de staaf M is en de lengte l, dan is het traagheidsmoment rond de as loodrecht op de lengte van de staaf en door het zwaartepunt ervan
java hoe te overschrijven

ik = ml 2 /12
Traagheidsmoment van een cirkel
Als de massa van de ring M is en de straal van de ring r is, dan is het traagheidsmoment rond de as die loodrecht op het midden van de ring loopt gelijk aan

ik = Dhr 2
Traagheidsmoment van een bol
Als een massieve bol een massa M en een straal r heeft, dan is het traagheidsmoment rond zijn diameter

I = 2/5 Dhr 2
Traagheidsmoment van massieve cilinder
Het traagheidsmoment van een massieve cilinder met straal ‘R’ en massa M wordt gegeven door

I = 1/2MR 2
Traagheidsmoment van holle cilinder
Een holle cilinder heeft twee stralen, namelijk de binnenradius en de buitenradius. Het traagheidsmoment van een holle cilinder met massa M, uitwendige straal R1en interne straal R2wordt gegeven als

ik = 1/2M(R 1 2 + R 2 2 )
Traagheidsmoment van vaste bol
Het traagheidsmoment van een massieve bol met massa ‘M’ en straal ‘R’ wordt gegeven als

I = 2/5MR 2
Traagheidsmoment van holle bol
Het traagheidsmoment van een holle bol met massa M en straal ‘R’ wordt gegeven als

I = 2/3MR 2
Traagheidsmoment van Ring
Het traagheidsmoment van een ring wordt gegeven voor twee gevallen waarin de rotatie-as door het midden gaat en wanneer de rotatie-as door de diameter gaat.
Het traagheidsmoment van de ring rond de as die door het midden gaat, wordt gegeven door
converteer tekenreeks naar int

ik = MR 2
Het traagheidsmoment van de ring rond de as die door de diameter gaat, wordt gegeven door

ik = Dhr 2 /2
Traagheidsmoment van het vierkant
Het traagheidsmoment van het vierkant van zijde ‘a’ wordt gegeven als

ik = een 4 /12
Het traagheidsmoment van een vierkante plaat van de zijde met lengte 'l' en massa M wordt gegeven als
I = 1/6ML 2
Traagheidsmoment van de driehoek
Het traagheidsmoment van een driehoek wordt gegeven voor 3 situaties: ten eerste wanneer de as door het midden gaat, ten tweede wanneer de as door de basis gaat en ten derde wanneer de as loodrecht op de basis staat. Laten we de formule voor hen een voor een bekijken. Voor een driehoek met basis ‘b’ en hoogte ‘h’ wordt de formule voor het traagheidsmoment als volgt gegeven

Wanneer de as door de Centroid gaat
ik = bh 3 /36
Wanneer de as door de basis gaat
ik = bh 3 /12
Wanneer de as loodrecht op de basis staat
ik = (hb/36)(geb 2 - B 1 b + b 1 2 )
Verschil tussen traagheidsmoment en traagheid
Het verschil tussen traagheid en traagheidsmoment wordt hieronder weergegeven:
| Ja nee. | Luiheid | Traagheidsmoment |
|---|---|---|
| 1. | Het belang ervan ligt in lineaire beweging. | Het belang ervan ligt in roterende beweging. |
| 2. | Het is die eigenschap van een object die de verandering van de toestand van het object in lineaire beweging tegenwerkt. | Het traagheidsmoment is die eigenschap van een object die de verandering van de toestand van het object tijdens een roterende beweging tegenwerkt. |
| 3. | De traagheid van een object hangt alleen af van zijn massa. | Het traagheidsmoment van een object hangt af van zijn massa en zijn massaverdeling ten opzichte van de rotatieas. |
| 4. | De traagheid van een object ligt vast. | Het traagheidsmoment van een object varieert met betrekking tot verschillende rotatieassen. |
Kinetische energie van roterend lichaam
Laten we aannemen dat een lichaam met massa ‘m’ roteert met snelheid v op een afstand ‘r’ van de rotatie-as. De hoeksnelheid wordt dan gegeven door ω = v/r en vervolgens v = rω. Nu weten we dat de Kinetische energie van een lichaam wordt gegeven door
KE = 1/2mv 2
⇒ KE = 1/2m(rω)2
⇒ KE = 1/2mr2Oh2
⇒ KE = 1/2Iω 2
Daarom wordt de kinetische energie van een roterend lichaam gegeven door de helft van het product van het traagheidsmoment en de hoeksnelheid van het lichaam. De kinetische energie van een roterend lichaam wordt ook wel genoemd Rotatiekinetische energie . De formule van Rotatiekinetische Energie wordt gegeven als
KE = 1/2Iω 2
Het traagheidsmoment (I) is onafhankelijk van de hoeksnelheid van het lichaam. Het is een functie van de massa van het roterende lichaam en de afstand van het lichaam tot de rotatieas. Daarom zien we dat hoekbeweging analoog is aan lineaire beweging. Dit betekent dat de betekenis van Traagheidsmoment is dat het een idee geeft over hoe massa's worden verdeeld op verschillende afstanden van de rotatie-as in een roterend lichaam.
Toepassing van traagheidsmoment
Moment of Inertia heeft verschillende toepassingen, waarvan sommige hieronder worden besproken:
- Door het grotere traagheidsmoment draait de aarde met dezelfde hoeksnelheid om haar as.
- Onder de kinderspeelmotor wordt een klein bewegend wiel geplaatst. Nadat dit wiel met de grond is gewreven en de motor is verlaten, blijft de motor vanwege het traagheidsmoment van het wiel nog enige tijd draaien.
- Elke motor bestaat uit een groot en zwaar wiel dat aan de as is bevestigd, met het grootste deel van zijn massa op de omtrek. Daarom is het traagheidsmoment hoog. Dit wiel wordt een vliegwiel genoemd. Het koppel dat de as van de motor aandrijft, blijft toenemen. Daarom is de rotatie van de as mogelijk niet uniform, maar door de aanwezigheid van een bewegend wiel met meer traagheid blijft de as met een vrijwel uniforme snelheid draaien.
- In het wiel van ossenkarren, riksja's, scooters, fietsen, enz. is het grootste deel van de massa geconcentreerd op de cirkel of rand. deze hoepel of routine wordt met stijve spaken aan de as van het wiel bevestigd. Door dit te doen neemt het traagheidsmoment toe. Wanneer de benen tijdens het fietsen niet meer bewegen, blijft het wiel dus nog enige tijd draaien.
Controleer ook
- Kinematica van rotatiebeweging
- Beweging van een star lichaam
- Rollende beweging
Opgeloste voorbeelden van traagheidsmomenten
Voorbeeld 1: Een lichaam met een massa van 500 g roteert om een as. de afstand van het massamiddelpunt van het lichaam tot de rotatieas is 1,2 m. Bereken het traagheidsmoment van het lichaam rond de rotatie-as.
Oplossing:
Gegeven dat M = 500 g = 0,5 kg, r = 1,2 m.
Uiteraard kan worden aangenomen dat de gehele massa van een lichaam zich in het massamiddelpunt bevindt. Dan het traagheidsmoment van het lichaam rond de rotatie-as.
ik = Dhr2
ik = 0,5 × (1,2)2
I = 0,72 kg·m2
Voorbeeld 2: De omwentelingsstraal rond een as op 12 cm afstand van het massamiddelpunt van een lichaam met een massa van 1,2 kg is 13 cm. Bereken de omwentelingsstraal en traagheidsmoment rond een as die door het massamiddelpunt gaat.
Oplossing:
Gegeven dat M = 1,0 kg, K = 13 cm, l = 12 cm, KCM=?, ikCM= ?
Van Stelling van Parallelle As I = ICM+ ml2
K2= KCM2+ l2
of KCM2= K2– l2
KCM2 = (13)2– (12)2= 25
subtekenreeks JavaKCM= 5
Nu, traagheidsmoment ICM= MKCM2
ICM= 1,0 × (0,05)2= 2,5×10-3kg m2
Voorbeeld 3: Een lichaam met een massa van 0,1 kg draait om een as. als de afstand van het massamiddelpunt van het lichaam tot de rotatieas 0,5 m is, zoek dan het traagheidsmoment van het lichaam.
Oplossing:
Gegeven dat M = 0,1 kg en r = 0,5 m
dus ik = meneer2
ik = 0,1 × (0,5)2
I = 0,025 kg·m2
Voorbeeld 4: Het traagheidsmoment van de ringen rond een as die door het midden gaat, loodrecht op het vlak van de cirkelvormige ring, is 200 g/cm 2 . Wat zal het traagheidsmoment zijn ten opzichte van de diameter?
Oplossing:
Traagheidsmoment van een cirkelvormige ring rond een as die door een ander centrum loodrecht op zijn vlak gaat
DHR2= 200 gram cm2
Traagheidsmoment ongeveer tot diameter
= 1/2 heer2
= 1/2 × 200 = 100 gram cm2
Veelgestelde vragen over momenten van traagheid
Hoe bereken je het traagheidsmoment?
De basisformule voor het vinden van het traagheidsmoment van een uniform object is:
ik = dhr 2
waar,
M is de massa van het object’
R is de afstand vanaf de rotatie-as
Hoe bereken je het traagheidsmoment van een balk?
Traagheidsmoment van een balk langs het midden en de as horizontaal daarop wordt berekend met behulp van de formule:
ik = ml 2 / 12
Waar hangt het traagheidsmoment van een lichaam van af?
Het traagheidsmoment van elk object hangt af van de onderstaande factoren:
- Massa van het lichaam,
- As van rotatie
- Vorm en grootte van het object
Wat is de eenheid van traagheidsmoment?
De eenheid van traagheidsmoment is kg 2
Kan het traagheidsmoment negatief zijn?
Nee, het traagheidsmoment kan nooit negatief zijn.
Wat is massatraagheidsmoment?
Massa-traagheidsmoment is de meting van de weerstand van een lichaam tegen verandering in zijn impulsmoment of richting. Het massatraagheidsmoment voor een puntmassa wordt gegeven door I = mr2en voor een systeem van deeltjes wordt het massatraagheidsmoment gegeven als I = ΣiMiRi2
Wat is het traagheidsmoment van het gebied?
Gebied Traagheidsmoment is een eigenschap van een 2D-vormvlak dat laat zien hoe punten verspreid zijn ten opzichte van een willekeurige as in een vlak. Gebiedstraagheidsmoment wordt ook wel tweede oppervlaktemoment of kwadratisch moment van oppervlakte genoemd. De formule voor het oppervlaktetraagheidsmoment in het xy-vlak wordt gegeven als Ixy= ∫xy dxdxy = ∫xy dA
