In de echte wereld machinaal leren toepassingen is het gebruikelijk dat er veel relevante kenmerken zijn, maar slechts een subset daarvan is waarneembaar. Bij het omgaan met variabelen die soms wel en soms niet waarneembaar zijn, is het inderdaad mogelijk om de gevallen waarin die variabele zichtbaar of waargenomen is te gebruiken om te leren en voorspellingen te doen voor de gevallen waarin deze niet waarneembaar is. Deze aanpak wordt vaak het omgaan met ontbrekende gegevens genoemd. Door gebruik te maken van de beschikbare gevallen waarin de variabele waarneembaar is, kunnen machine learning-algoritmen patronen en relaties leren uit de waargenomen gegevens. Deze aangeleerde patronen kunnen vervolgens worden gebruikt om de waarden van de variabele te voorspellen in gevallen waarin deze ontbreekt of niet waarneembaar is.
Het verwachtingsmaximalisatie-algoritme kan worden gebruikt om situaties aan te pakken waarin variabelen gedeeltelijk waarneembaar zijn. Wanneer bepaalde variabelen waarneembaar zijn, kunnen we die instanties gebruiken om hun waarden te leren en te schatten. Vervolgens kunnen we de waarden van deze variabelen voorspellen in gevallen waarin deze niet waarneembaar zijn.
Het EM-algoritme werd voorgesteld en genoemd in een baanbrekend artikel dat in 1977 werd gepubliceerd door Arthur Dempster, Nan Laird en Donald Rubin. Hun werk formaliseerde het algoritme en demonstreerde het nut ervan bij statistische modellering en schattingen.
Het EM-algoritme is toepasbaar op latente variabelen, dit zijn variabelen die niet direct waarneembaar zijn, maar worden afgeleid uit de waarden van andere waargenomen variabelen. Door gebruik te maken van de bekende algemene vorm van de waarschijnlijkheidsverdeling die deze latente variabelen beheerst, kan het EM-algoritme hun waarden voorspellen.
Het EM-algoritme dient als basis voor veel onbewaakte clusteralgoritmen op het gebied van machinaal leren. Het biedt een raamwerk om de lokale maximale waarschijnlijkheidsparameters van een statistisch model te vinden en latente variabelen af te leiden in gevallen waarin gegevens ontbreken of onvolledig zijn.
Verwachtingsmaximalisatie (EM) algoritme
Het Expectation-Maximization (EM)-algoritme is een iteratieve optimalisatiemethode die verschillende onbewaakte optimalisatiemethoden combineert machinaal leren algoritmen om maximale waarschijnlijkheid of maximale posterieure schattingen van parameters te vinden in statistische modellen waarbij niet-waargenomen latente variabelen betrokken zijn. Het EM-algoritme wordt vaak gebruikt voor modellen van latente variabelen en kan ontbrekende gegevens verwerken. Het bestaat uit een schattingsstap (E-stap) en een maximalisatiestap (M-stap), die een iteratief proces vormen om de pasvorm van het model te verbeteren.
- In de E-stap berekent het algoritme de latente variabelen, d.w.z. de verwachting van de log-waarschijnlijkheid, met behulp van de huidige parameterschattingen.
- In de M-stap bepaalt het algoritme de parameters die de verwachte log-waarschijnlijkheid maximaliseren die in de E-stap wordt verkregen, en overeenkomstige modelparameters worden bijgewerkt op basis van de geschatte latente variabelen.

Verwachtingsmaximalisatie in EM-algoritme
Door deze stappen iteratief te herhalen, probeert het EM-algoritme de waarschijnlijkheid van de waargenomen gegevens te maximaliseren. Het wordt vaak gebruikt voor leertaken zonder toezicht, zoals clustering, waarbij latente variabelen worden afgeleid en heeft toepassingen op verschillende gebieden, waaronder machinaal leren, computervisie en natuurlijke taalverwerking.
Sleutelbegrippen in het verwachtingsmaximalisatie-algoritme (EM).
Enkele van de meest gebruikte sleuteltermen in het Expectation-Maximization (EM)-algoritme zijn als volgt:
- Latente variabelen: Latente variabelen zijn niet-waargenomen variabelen in statistische modellen die alleen indirect kunnen worden afgeleid via hun effecten op waarneembare variabelen. Ze kunnen niet direct worden gemeten, maar kunnen worden gedetecteerd aan de hand van hun impact op de waarneembare variabelen. Waarschijnlijkheid: Het is de waarschijnlijkheid dat de gegeven gegevens worden waargenomen, gegeven de parameters van het model. In het EM-algoritme is het doel om de parameters te vinden die de waarschijnlijkheid maximaliseren. Log-waarschijnlijkheid: Het is de logaritme van de waarschijnlijkheidsfunctie, die de mate van overeenstemming tussen de waargenomen gegevens en het model meet. Het EM-algoritme probeert de logwaarschijnlijkheid te maximaliseren. Maximale waarschijnlijkheidsschatting (MLE): MLE is een methode om de parameters van een statistisch model te schatten door de parameterwaarden te vinden die de waarschijnlijkheidsfunctie maximaliseren, die meet hoe goed het model de waargenomen gegevens verklaart. Posterieure waarschijnlijkheid: In de context van Bayesiaanse inferentie kan het EM-algoritme worden uitgebreid om de maximale a posteriori (MAP) schattingen te schatten, waarbij de posterieure waarschijnlijkheid van de parameters wordt berekend op basis van de eerdere verdeling en de waarschijnlijkheidsfunctie. Verwachtingsstap (E): De E-stap van het EM-algoritme berekent de verwachte waarde of de posterieure waarschijnlijkheid van de latente variabelen, gegeven de waargenomen gegevens en huidige parameterschattingen. Het omvat het berekenen van de kansen van elke latente variabele voor elk datapunt. Maximalisatiestap (M): De M-stap van het EM-algoritme werkt de parameterschattingen bij door de verwachte logwaarschijnlijkheid verkregen uit de E-stap te maximaliseren. Het gaat om het vinden van de parameterwaarden die de waarschijnlijkheidsfunctie optimaliseren, meestal via numerieke optimalisatiemethoden. Convergentie: Convergentie verwijst naar de toestand waarin het EM-algoritme een stabiele oplossing heeft bereikt. Het wordt doorgaans bepaald door te controleren of de verandering in de logwaarschijnlijkheid of de parameterschattingen onder een vooraf gedefinieerde drempel valt.
Hoe het verwachtingsmaximalisatie-algoritme (EM) werkt:
De essentie van het Expectation-Maximization-algoritme is om de beschikbare waargenomen gegevens van de dataset te gebruiken om de ontbrekende gegevens te schatten en die gegevens vervolgens te gebruiken om de waarden van de parameters bij te werken. Laten we het EM-algoritme in detail begrijpen.

EM-algoritme stroomdiagram
- Initialisatie:
- In eerste instantie wordt een reeks initiële waarden van de parameters in beschouwing genomen. Er wordt een reeks onvolledige waargenomen gegevens aan het systeem gegeven, in de veronderstelling dat de waargenomen gegevens afkomstig zijn van een specifiek model.
- Bereken de posterieure waarschijnlijkheid of verantwoordelijkheid van elke latente variabele, gegeven de waargenomen gegevens en huidige parameterschattingen.
- Schat de ontbrekende of onvolledige gegevenswaarden met behulp van de huidige parameterschattingen.
- Bereken de logwaarschijnlijkheid van de waargenomen gegevens op basis van de huidige parameterschattingen en geschatte ontbrekende gegevens.
- Werk de parameters van het model bij door de verwachte volledige datalog-waarschijnlijkheid verkregen uit de E-step te maximaliseren.
- Dit omvat doorgaans het oplossen van optimalisatieproblemen om de parameterwaarden te vinden die de logwaarschijnlijkheid maximaliseren.
- Welke specifieke optimalisatietechniek wordt gebruikt, hangt af van de aard van het probleem en het gebruikte model.
- Controleer op convergentie door de verandering in log-waarschijnlijkheid of de parameterwaarden tussen iteraties te vergelijken.
- Als de verandering onder een vooraf gedefinieerde drempel ligt, stop dan en beschouw het algoritme als geconvergeerd.
- Ga anders terug naar de E-stap en herhaal het proces totdat convergentie is bereikt.
Verwachtingsmaximalisatie-algoritme Stap voor stap implementatie
Importeer de benodigde bibliotheken
Python3
import> numpy as np> import> matplotlib.pyplot as plt> from> scipy.stats>import> norm> |
>
exemplaarvan
>
Genereer een gegevensset met twee Gauss-componenten
Python3
# Generate a dataset with two Gaussian components> mu1, sigma1>=> 2>,>1> mu2, sigma2>=> ->1>,>0.8> X1>=> np.random.normal(mu1, sigma1, size>=>200>)> X2>=> np.random.normal(mu2, sigma2, size>=>600>)> X>=> np.concatenate([X1, X2])> # Plot the density estimation using seaborn> sns.kdeplot(X)> plt.xlabel(>'X'>)> plt.ylabel(>'Density'>)> plt.title(>'Density Estimation of X'>)> plt.show()> |
JavaScript-trim-subtekenreeks
>
>
Uitvoer :

Dichtheidsdiagram
Initialiseer parameters
Python3
# Initialize parameters> mu1_hat, sigma1_hat>=> np.mean(X1), np.std(X1)> mu2_hat, sigma2_hat>=> np.mean(X2), np.std(X2)> pi1_hat, pi2_hat>=> len>(X1)>/> len>(X),>len>(X2)>/> len>(X)> |
>
>
Voer het EM-algoritme uit
- Itereert voor het opgegeven aantal tijdperken (20 in dit geval).
- In elk tijdperk berekent de E-step de verantwoordelijkheden (gammawaarden) door de Gaussiaanse waarschijnlijkheidsdichtheden voor elke component te evalueren en deze te wegen met de overeenkomstige verhoudingen.
- De M-stap werkt de parameters bij door het gewogen gemiddelde en de standaardafwijking voor elke component te berekenen
Python3
# Perform EM algorithm for 20 epochs> num_epochs>=> 20> log_likelihoods>=> []> for> epoch>in> range>(num_epochs):> ># E-step: Compute responsibilities> >gamma1>=> pi1_hat>*> norm.pdf(X, mu1_hat, sigma1_hat)> >gamma2>=> pi2_hat>*> norm.pdf(X, mu2_hat, sigma2_hat)> >total>=> gamma1>+> gamma2> >gamma1>/>=> total> >gamma2>/>=> total> > ># M-step: Update parameters> >mu1_hat>=> np.>sum>(gamma1>*> X)>/> np.>sum>(gamma1)> >mu2_hat>=> np.>sum>(gamma2>*> X)>/> np.>sum>(gamma2)> >sigma1_hat>=> np.sqrt(np.>sum>(gamma1>*> (X>-> mu1_hat)>*>*>2>)>/> np.>sum>(gamma1))> >sigma2_hat>=> np.sqrt(np.>sum>(gamma2>*> (X>-> mu2_hat)>*>*>2>)>/> np.>sum>(gamma2))> >pi1_hat>=> np.mean(gamma1)> >pi2_hat>=> np.mean(gamma2)> > ># Compute log-likelihood> >log_likelihood>=> np.>sum>(np.log(pi1_hat>*> norm.pdf(X, mu1_hat, sigma1_hat)> >+> pi2_hat>*> norm.pdf(X, mu2_hat, sigma2_hat)))> >log_likelihoods.append(log_likelihood)> # Plot log-likelihood values over epochs> plt.plot(>range>(>1>, num_epochs>+>1>), log_likelihoods)> plt.xlabel(>'Epoch'>)> plt.ylabel(>'Log-Likelihood'>)> plt.title(>'Log-Likelihood vs. Epoch'>)> plt.show()> |
>
>
Uitvoer :

Epoch versus log-waarschijnlijkheid
Teken de uiteindelijke geschatte dichtheid
Python3
char tostring java
# Plot the final estimated density> X_sorted>=> np.sort(X)> density_estimation>=> pi1_hat>*>norm.pdf(X_sorted,> >mu1_hat,> >sigma1_hat)>+> pi2_hat>*> norm.pdf(X_sorted,> >mu2_hat,> >sigma2_hat)> plt.plot(X_sorted, gaussian_kde(X_sorted)(X_sorted), color>=>'green'>, linewidth>=>2>)> plt.plot(X_sorted, density_estimation, color>=>'red'>, linewidth>=>2>)> plt.xlabel(>'X'>)> plt.ylabel(>'Density'>)> plt.title(>'Density Estimation of X'>)> plt.legend([>'Kernel Density Estimation'>,>'Mixture Density'>])> plt.show()> |
>
>
Uitvoer :
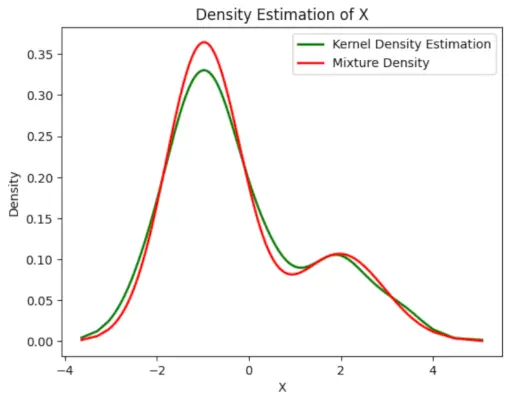
Geschatte dichtheid
Toepassingen van de EM-algoritme
- Het kan worden gebruikt om de ontbrekende gegevens in een monster aan te vullen.
- Het kan worden gebruikt als basis voor het onbewaakt leren van clusters.
- Het kan worden gebruikt voor het schatten van de parameters van het Hidden Markov Model (HMM).
- Het kan worden gebruikt voor het ontdekken van de waarden van latente variabelen.
Voordelen van EM-algoritme
- Het is altijd gegarandeerd dat de waarschijnlijkheid met elke iteratie toeneemt.
- De E-step en M-step zijn qua implementatie vaak vrij eenvoudig voor veel problemen.
- Oplossingen voor de M-stappen bestaan vaak in gesloten vorm.
Nadelen van EM-algoritme
- Het kent een langzame convergentie.
- Het maakt alleen convergentie naar de lokale optima mogelijk.
- Het vereist zowel de kansen, voorwaarts als achterwaarts (numerieke optimalisatie vereist alleen voorwaartse waarschijnlijkheid).
