Gegeven een 3D-array arr[l][m][n] is het de taak om de minimale padsom te vinden van de eerste cel van de array naar de laatste cel van de array. We kunnen alleen naar een aangrenzend element gaan, d.w.z. vanuit een gegeven cel (ij k) kunnen cellen (i+1 j k) (i j+1 k) en (ij k+1) worden doorlopen. Diagonaal doorlopen is niet toegestaan. We mogen aannemen dat alle kosten positieve gehele getallen zijn.
Voorbeelden:
Input : arr[][][]= { {{1 2} {3 4}} {{4 8} {5 2}} }; Output : 9 Explanation : arr[0][0][0] + arr[0][0][1] + arr[0][1][1] + arr[1][1][1] Input : { { {1 2} {4 3}} { {3 4} {2 1}} }; Output : 7 Explanation : arr[0][0][0] + arr[0][0][1] + arr[0][1][1] + arr[1][1][1] Laten we een 3D-array arr[2][2][2] beschouwen, weergegeven door een balk met waarden als:
arr[][][] = {{{1 2} {3 4}} { {4 8} {5 2}}}; Result = 9 is calculated as: 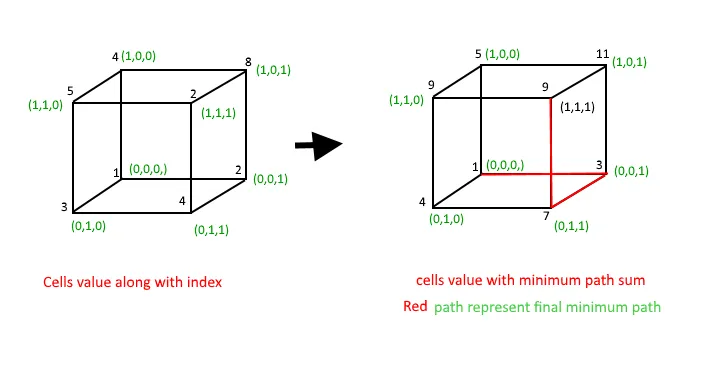
Dit probleem is vergelijkbaar met Min. kostenpad. en kan worden opgelost met behulp van dynamisch programmeren.
// Array for storing result int tSum[l][m][n]; tSum[0][0][0] = arr[0][0][0]; /* Initialize first row of tSum array */ for (i = 1; i < l; i++) tSum[i][0][0] = tSum[i-1][0][0] + arr[i][0][0]; /* Initialize first column of tSum array */ for (j = 1; j < m; j++) tSum[0][j][0] = tSum[0][j-1][0] + arr[0][j][0]; /* Initialize first width of tSum array */ for (k = 1; k < n; k++) tSum[0][0][k] = tSum[0][0][k-1] + arr[0][0][k]; /* Initialize first row- First column of tSum array */ for (i = 1; i < l; i++) for (j = 1; j < m; j++) tSum[i][j][0] = min(tSum[i-1][j][0] tSum[i][j-1][0] INT_MAX) + arr[i][j][0]; /* Initialize first row- First width of tSum array */ for (i = 1; i < l; i++) for (k = 1; k < n; k++) tSum[i][0][k] = min(tSum[i-1][0][k] tSum[i][0][k-1] INT_MAX) + arr[i][0][k]; /* Initialize first width- First column of tSum array */ for (k = 1; k < n; k++) for (j = 1; j < m; j++) tSum[0][j][k] = min(tSum[0][j][k-1] tSum[0][j-1][k] INT_MAX) + arr[0][j][k]; /* Construct rest of the tSum array */ for (i = 1; i < l; i++) for (j = 1; j < m; j++) for (k = 1; k < n; k++) tSum[i][j][k] = min(tSum[i-1][j][k] tSum[i][j-1][k] tSum[i][j][k-1]) + arr[i][j][k]; return tSum[l-1][m-1][n-1];C++
// C++ program for Min path sum of 3D-array #include
// Java program for Min path sum of 3D-array import java.io.*; class GFG { static int l =3; static int m =3; static int n =3; // A utility function that returns minimum // of 3 integers static int min(int x int y int z) { return (x < y)? ((x < z)? x : z) : ((y < z)? y : z); } // function to calculate MIN path sum of 3D array static int minPathSum(int arr[][][]) { int i j k; int tSum[][][] =new int[l][m][n]; tSum[0][0][0] = arr[0][0][0]; /* Initialize first row of tSum array */ for (i = 1; i < l; i++) tSum[i][0][0] = tSum[i-1][0][0] + arr[i][0][0]; /* Initialize first column of tSum array */ for (j = 1; j < m; j++) tSum[0][j][0] = tSum[0][j-1][0] + arr[0][j][0]; /* Initialize first width of tSum array */ for (k = 1; k < n; k++) tSum[0][0][k] = tSum[0][0][k-1] + arr[0][0][k]; /* Initialize first row- First column of tSum array */ for (i = 1; i < l; i++) for (j = 1; j < m; j++) tSum[i][j][0] = min(tSum[i-1][j][0] tSum[i][j-1][0] Integer.MAX_VALUE) + arr[i][j][0]; /* Initialize first row- First width of tSum array */ for (i = 1; i < l; i++) for (k = 1; k < n; k++) tSum[i][0][k] = min(tSum[i-1][0][k] tSum[i][0][k-1] Integer.MAX_VALUE) + arr[i][0][k]; /* Initialize first width- First column of tSum array */ for (k = 1; k < n; k++) for (j = 1; j < m; j++) tSum[0][j][k] = min(tSum[0][j][k-1] tSum[0][j-1][k] Integer.MAX_VALUE) + arr[0][j][k]; /* Construct rest of the tSum array */ for (i = 1; i < l; i++) for (j = 1; j < m; j++) for (k = 1; k < n; k++) tSum[i][j][k] = min(tSum[i-1][j][k] tSum[i][j-1][k] tSum[i][j][k-1]) + arr[i][j][k]; return tSum[l-1][m-1][n-1]; } // Driver program public static void main (String[] args) { int arr[][][] = { { {1 2 4} {3 4 5} {5 2 1}} { {4 8 3} {5 2 1} {3 4 2}} { {2 4 1} {3 1 4} {6 3 8}} }; System.out.println ( minPathSum(arr)); } } // This code is contributed by vt_m
# Python3 program for Min # path sum of 3D-array l = 3 m = 3 n = 3 # A utility function # that returns minimum # of 3 integers def Min(x y z): return min(min(xy)z) # function to calculate MIN # path sum of 3D array def minPathSum(arr): tSum = [[[0 for k in range(n)]for j in range(m)] for i in range(l)] tSum[0][0][0] = arr[0][0][0] # Initialize first # row of tSum array for i in range(1l): tSum[i][0][0] = tSum[i - 1][0][0] + arr[i][0][0] # Initialize first column # of tSum array for j in range(1m): tSum[0][j][0] = tSum[0][j - 1][0] + arr[0][j][0] # Initialize first # width of tSum array for k in range(1n): tSum[0][0][k] = tSum[0][0][k - 1] + arr[0][0][k] # Initialize first # row- First column of # tSum array for i in range(1l): for j in range(1m): tSum[i][j][0] = Min(tSum[i - 1][j][0]tSum[i][j - 1][0]1000000000) + arr[i][j][0]; # Initialize first # row- First width of # tSum array for i in range(1l): for k in range(1n): tSum[i][0][k] = Min(tSum[i - 1][0][k]tSum[i][0][k - 1]1000000000) + arr[i][0][k] # Initialize first # width- First column of # tSum array for k in range(1n): for j in range(1m): tSum[0][j][k] = Min(tSum[0][j][k - 1]tSum[0][j - 1][k]1000000000) + arr[0][j][k] # Construct rest of # the tSum array for i in range(1l): for j in range(1m): for k in range(1n): tSum[i][j][k] = Min(tSum[i - 1][j][k]tSum[i][j - 1][k]tSum[i][j][k - 1]) + arr[i][j][k] return tSum[l-1][m-1][n-1] # Driver Code arr = [[[1 2 4] [3 4 5] [5 2 1]] [[4 8 3] [5 2 1] [3 4 2]] [[2 4 1] [3 1 4] [6 3 8]]] print(minPathSum(arr)) # This code is contributed by shinjanpatra
// C# program for Min // path sum of 3D-array using System; class GFG { static int l = 3; static int m = 3; static int n = 3; // A utility function // that returns minimum // of 3 integers static int min(int x int y int z) { return (x < y) ? ((x < z) ? x : z) : ((y < z) ? y : z); } // function to calculate MIN // path sum of 3D array static int minPathSum(int []arr) { int i j k; int [ ]tSum = new int[l m n]; tSum[0 0 0] = arr[0 0 0]; /* Initialize first row of tSum array */ for (i = 1; i < l; i++) tSum[i 0 0] = tSum[i - 1 0 0] + arr[i 0 0]; /* Initialize first column of tSum array */ for (j = 1; j < m; j++) tSum[0 j 0] = tSum[0 j - 1 0] + arr[0 j 0]; /* Initialize first width of tSum array */ for (k = 1; k < n; k++) tSum[0 0 k] = tSum[0 0 k - 1] + arr[0 0 k]; /* Initialize first row- First column of tSum array */ for (i = 1; i < l; i++) for (j = 1; j < m; j++) tSum[i j 0] = min(tSum[i - 1 j 0] tSum[i j - 1 0] int.MaxValue) + arr[i j 0]; /* Initialize first row- First width of tSum array */ for (i = 1; i < l; i++) for (k = 1; k < n; k++) tSum[i 0 k] = min(tSum[i - 1 0 k] tSum[i 0 k - 1] int.MaxValue) + arr[i 0 k]; /* Initialize first width- First column of tSum array */ for (k = 1; k < n; k++) for (j = 1; j < m; j++) tSum[0 j k] = min(tSum[0 j k - 1] tSum[0 j - 1 k] int.MaxValue) + arr[0 j k]; /* Construct rest of the tSum array */ for (i = 1; i < l; i++) for (j = 1; j < m; j++) for (k = 1; k < n; k++) tSum[i j k] = min(tSum[i - 1 j k] tSum[i j - 1 k] tSum[i j k - 1]) + arr[i j k]; return tSum[l-1m-1n-1]; } // Driver Code static public void Main () { int [ ]arr= {{{1 2 4} {3 4 5} {5 2 1}} {{4 8 3} {5 2 1} {3 4 2}} {{2 4 1} {3 1 4} {6 3 8}}}; Console.WriteLine(minPathSum(arr)); } } // This code is contributed by ajit
<script> // Javascript program for Min // path sum of 3D-array var l = 3; var m = 3; var n = 3; // A utility function // that returns minimum // of 3 integers function min(x y z) { return (x < y) ? ((x < z) ? x : z) : ((y < z) ? y : z); } // function to calculate MIN // path sum of 3D array function minPathSum(arr) { var i j k; var tSum = Array(l); for(var i = 0; i<l;i++) { tSum[i] = Array.from(Array(m) ()=>Array(n)); } tSum[0][0][0] = arr[0][0][0]; /* Initialize first row of tSum array */ for (i = 1; i < l; i++) tSum[i][0][0] = tSum[i - 1][0][0] + arr[i][0][0]; /* Initialize first column of tSum array */ for (j = 1; j < m; j++) tSum[0][j][0] = tSum[0][j - 1][0] + arr[0][j][0]; /* Initialize first width of tSum array */ for (k = 1; k < n; k++) tSum[0][0][k] = tSum[0][0][k - 1] + arr[0][0][k]; /* Initialize first row- First column of tSum array */ for (i = 1; i < l; i++) for (j = 1; j < m; j++) tSum[i][j][0] = min(tSum[i - 1][j][0] tSum[i][j - 1][0] 1000000000) + arr[i][j][0]; /* Initialize first row- First width of tSum array */ for (i = 1; i < l; i++) for (k = 1; k < n; k++) tSum[i][0][k] = min(tSum[i - 1][0][k] tSum[i][0][k - 1] 1000000000) + arr[i][0][k]; /* Initialize first width- First column of tSum array */ for (k = 1; k < n; k++) for (j = 1; j < m; j++) tSum[0][j][k] = min(tSum[0][j][k - 1] tSum[0][j - 1][k] 1000000000) + arr[0][j][k]; /* Construct rest of the tSum array */ for (i = 1; i < l; i++) for (j = 1; j < m; j++) for (k = 1; k < n; k++) tSum[i][j][k] = min(tSum[i - 1][j][k] tSum[i][j - 1][k] tSum[i][j][k - 1]) + arr[i][j][k]; return tSum[l-1][m-1][n-1]; } // Driver Code var arr= [[[1 2 4] [3 4 5] [5 2 1]] [[4 8 3] [5 2 1] [3 4 2]] [[2 4 1] [3 1 4] [6 3 8]]]; document.write(minPathSum(arr)); </script>
Uitgang:
20
Tijdcomplexiteit: O(l*m*n)
Hulpruimte: O(l*m*n)
