De hoek tussen twee vectoren is de hoek tussen hun staarten en deze hoek kan eenvoudig worden gevonden met behulp van het kruisproduct en het puntproduct van vectorformules. De hoek tussen twee vectoren ligt altijd tussen 0° en 180°.
In dit artikel zullen we in detail leren over de hoek tussen twee vectoren, definitie, formules en voorbeelden.
Wat is de hoek tussen twee vectoren?
De hoek tussen twee vectoren is de hoek gevormd op het snijpunt van hun staarten. De hoek tussen twee vectoren kan acuut, rechts of stomp zijn, afhankelijk van de richting van de vectoren.
De hoek tussen twee vectoren wordt gevonden met behulp van twee formules:
- Met behulp van het puntproduct van vectoren
- Kruisproduct van vectoren gebruiken
Dit wordt uitgelegd in onderstaande formule.
Hoek tussen twee vectorformules
Hoek tussen twee vectoren wordt gemakkelijk en meestal gevonden met behulp van scalair product van vectoren.

Twee vectoren A en B
Punt product van A en B wordt gegeven door,
vec{A}.vec{B} = |EEN| |B| cosθ.
Speciale gevallen
- Wanneer de hoek tussen vectoren 0 graden is.
Dat is θ = 0°
⇒ |A| |B| cosθ
⇒ |A| |B| cos0°
⇒ |A| |B| [cos0° = 1]
- Wanneer de hoek tussen vectoren 180 graden is.
⇒ |A| |B| cosθ
⇒ |A| |B| cos180°
⇒ – |A| |B| [cos180° = -1]
- Wanneer de hoek tussen vectoren 90 graden is.
⇒ |A| |B| cosθ
⇒ |A| |B| cos90°
⇒ |A| |B| × 0 [cos90° = 0]
⇒ 0
Formule voor hoek tussen twee vectoren
De cosinus van de hoek tussen twee vectoren is gelijk aan de som van het product van de individuele bestanddelen van de twee vectoren, gedeeld door het product van de grootte van de twee vectoren.
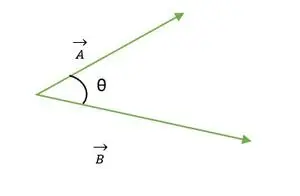
Twee vectoren A en B
cosθ=
θ= cos-1
In cartesiaanse vorm,
EEN = EENXik + AEnj+AMetk
B=BXik + BEnj + BMetk
cos θ =
frac{(Ax.Bx+Ay.By+Az.Bz)}{(sqrt{Ax^2+Ay^2+Az^2}×sqrt{Bx^2+By^2+Bz^2})}
Eigenschappen van Dot-product
- Het puntproduct is commutatief
vec{A}.vec{B}=vec{B}.vec{A}
- Dot-product is distributief
vec{A}.(vec{B}+vec{C})=(vec{A}.vec{B}+vec{A}.vec{C})
De hoek tussen twee vectoren ligt tussen 0 ≤ θ ≤ 180. Wanneer de staarten of koppen van beide vectoren samenvallen, wordt de hoek tussen vectoren berekend.
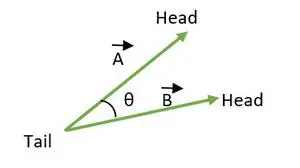
Staart valt samen
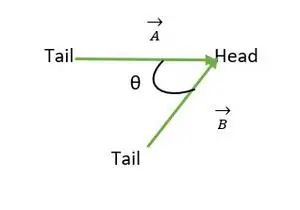
Hoofd samenvallen
Voorbeeldproblemen Hoek tussen formule voor twee vectoren
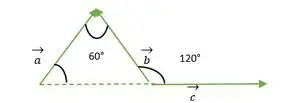
Probleem 1: Vind de hoek tussen vectoren (als ze een gelijkzijdige driehoek vormen)
- a- en b-vectoren
- b- en c-vectoren
- a- en c-vectoren
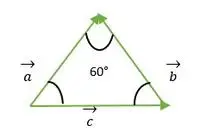
Gelijkzijdige driehoek gevormd door a, b, c vector
Oplossing:
- a- en b-vectoren
Voor vector a en b valt de kop van beide vectoren met elkaar samen, dus de hoek tussen de vector a en b is hetzelfde als de hoek tussen twee zijden van een gelijkzijdige driehoek = 60 °.
- b- en c-vectoren:
Uit de bovenstaande figuur zien we dat kop of staart van de b- en c-vector niet met elkaar samenvallen.
Dus door de eigenschap te gebruiken: Een vector blijft ongewijzigd als deze parallel aan zichzelf wordt verzonden.
Vector c wordt evenwijdig aan zichzelf verschoven
Nu zien we dat de staart van vectoren b en c met elkaar samenvallen, en daarom hetzelfde is als de buitenhoek bij een gelijkzijdige driehoek = 120°.
- a- en c-vectoren
De staart van a en c vallen samen
Voor vectoren a en c valt de staart van beide vectoren met elkaar samen, daarom is de hoek tussen de vectoren a en c hetzelfde als de hoek tussen twee zijden van de gelijkzijdige driehoek = 60°.
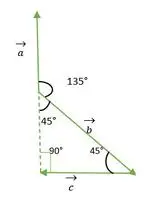
Probleem 2: Vind hoeken tussen vectoren als ze een gelijkbenige rechthoekige driehoek vormen.
Python-padinstelling
- a en b-vector
- b en c-vector
- a- en c-vectoren
Oplossing:
- a en b-vector
Rechte hoek Gelijkbenige driehoek
Uit de bovenstaande figuur zien we dat de kop of de staart van de vectoren a en b niet met elkaar samenvallen. Dus door de eigenschap te gebruiken: Een vector blijft ongewijzigd als deze parallel aan zichzelf wordt verzonden.
een vector wordt evenwijdig aan zichzelf verschoven
Nu vallen de staarten van a- en b-vectoren met elkaar samen en maken een hoek die hetzelfde is als de buitenhoek van een rechthoekige gelijkbenige driehoek = 135°.
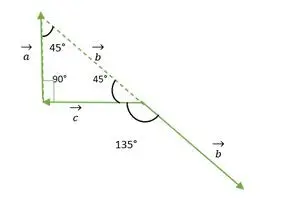
- b en c-vector
Rechte hoek Gelijkbenige driehoek
Uit de bovenstaande figuur valt de vectorkop of -staart van b en c niet met elkaar samen. Door deze eigenschap te gebruiken, blijft een vector dus ongewijzigd als deze parallel aan zichzelf wordt verzonden.
b-vector wordt parallel aan zichzelf verschoven
Nu vallen de staarten van de b- en c-vectoren met elkaar samen en maken een hoek die gelijk is aan de buitenhoek van een rechthoekige gelijkbenige driehoek = 135°.
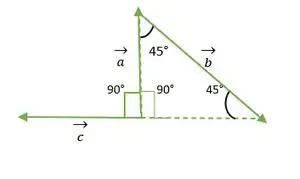
- a- en c-vectoren
Rechte hoek Gelijkbenige driehoek
Uit de bovenstaande figuur vallen de vectorkop of -staarten van a en c niet met elkaar samen. Dus door de eigenschap te gebruiken: Een vector blijft ongewijzigd als deze parallel aan zichzelf wordt verzonden.
c-vector wordt parallel aan zichzelf verplaatst
Nu vallen de staarten van de vectoren a en c met elkaar samen en maken een hoek die hetzelfde is als de rechte hoek van een gelijkbenige driehoek = 90°.
Opgave 3: Vind de hoek tussen de vectoren A = i + j + k en vector B = -2i – 2j – 2k.
Oplossing:
Uit de formule,
EEN = EENXik + AEnj+AMetk
B=BXik + BEnj + BMetk
cosθ=
frac{(Ax.Bx+Ay.By+Az.Bz)}{(sqrt{Ax^2+Ay^2+Az^2}×sqrt{Bx^2+By^2+Bz^2})} Hier in de gegeven vraag,
A= ik + j + k
B= -2i -2j -2k
De waarden in de formule vervangen
⇒ cosθ =
frac{(1.(-2)+1.(-2)+1.(-2))}{(sqrt{1^2+1^2+1^2}×sqrt{(-2)^2+(-2)^2+(-2)^2})} ⇒ cosθ =
frac{(-2-2-2)}{(sqrt{1+1+1}×sqrt{4+4+4})} ⇒ cosθ =
frac{-6}{(sqrt{3}×sqrt{12})} ⇒ cosθ =
frac{-6}{(sqrt{36})} ⇒ cosθ = -6/6
⇒ cosθ= -1
⇒ θ = 180°
Opgave 4: Vind de hoek tussen vector A = 3i + 4j en B = 2i + j
Oplossing:
soorten binaire bomen
EEN = EENXik + AEnj+AMetk
B = BXik + BEnj + BMetk
cosθ =
frac{(Ax.Bx+Ay.By+Az.Bz)}{(sqrt{Ax^2+Ay^2+Az^2}×sqrt{Bx^2+By^2+Bz^2})} Hier gegeven,
A= 3i + 4j + 0k
B= 2i + j + 0k
Vervanging van de waarden in de formule,
⇒ cosθ =
frac{(3.2+4.1+0.0)}{(sqrt{3^2+4^2+0^2}×sqrt{2^2+1^2+0^2})} ⇒ cosθ =
frac{(6+4+0)}{(sqrt{9+16+0}×sqrt{4+1+0})} ⇒ cosθ =
frac{(10)}{(sqrt{25}×sqrt{5})} ⇒ cosθ =
frac{(10)}{(sqrt{125})} ⇒ θ = cos-1(
frac{(10)}{5.(sqrt{5})} )⇒ θ = cos-1(
frac{2}{(sqrt{5})} )
Opgave 5: Vind de hoek tussen vector A = i + j en vector B = j + k.
Oplossing:
Uit de formule,
EEN = EENXik + AEnj+AMetk
B = BXik + BEnj + BMetk
cosθ =
frac{(Ax.Bx+Ay.By+Az.Bz)}{(sqrt{Ax^2+Ay^2+Az^2}×sqrt{Bx^2+By^2+Bz^2})} Hier in de gegeven vraag,
⇒ EEN = ik + j
⇒ B = j + k
⇒ cosθ =
frac{(1.0+1.1+0.1)}{(sqrt{1^2+1^2+0^2}×sqrt{0^2+1^2+1^2})} ⇒ cosθ =
frac{(1)}{(sqrt{1+1+0}×sqrt{0+1+1})} ⇒ cosθ =
frac{1}{(sqrt{2}×sqrt{2})} ⇒ θ = cos-1(1/2)
⇒ θ = 60°