Gegeven twee snaren, S1 En S2 , is het de taak om de lengte van de langste gemeenschappelijke deelreeks te vinden, d.w.z. de langste deelreeks die in beide strings aanwezig is.
A langste gemeenschappelijke deelreeks (LCS) wordt gedefinieerd als de langste deelreeks die gemeenschappelijk is in alle gegeven invoerreeksen.
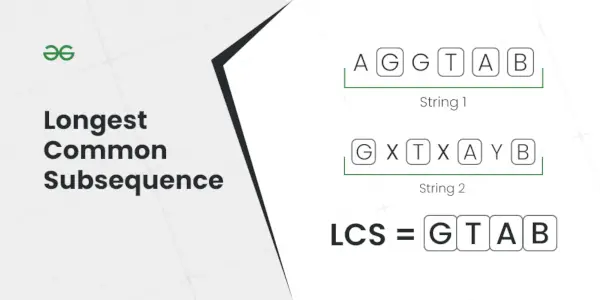
Langste gemeenschappelijke vervolgreeks
Voorbeelden:
Aanbevolen praktijk Langste gebruikelijke vervolgreeks Probeer het!Invoer: S1 = ABC, S2 = ACD
Uitgang: 2
Uitleg: De langste deelreeks die in beide strings aanwezig is, is AC.Invoer: S1 = AGGTAB, S2 = GXTXAYB
Uitgang: 4
Uitleg: De langste veel voorkomende deelreeks is GTAB.Invoer: S1 = ABC, S2 = KBA
Uitgang: 1
Uitleg: Er zijn drie gemeenschappelijke deelreeksen met een lengte van 1, A, B en C, en geen gemeenschappelijke deelreeks met een lengte van meer dan 1.Invoer: S1 = XYZW, S2 = XYWZ
Uitgang: 3
Uitleg: Er zijn twee gemeenschappelijke deelreeksen met lengte 3, XYZ en XYW, en geen gemeenschappelijke deelreeks. met een lengte van meer dan 3.
Langste gemeenschappelijke subreeks (LCS) met behulp van recursie:
Genereer alle mogelijke subreeksen en vind de langste daarvan die in beide strings aanwezig is met behulp van Volg de onderstaande stappen om het idee te implementeren:
- Maak een recursieve functie [zeg lcs() ].
- Controleer de relatie tussen de eerste tekens van de strings die nog niet zijn verwerkt.
- Afhankelijk van de relatie roept u de volgende recursieve functie op zoals hierboven vermeld.
- Retourneer de lengte van de ontvangen LCS als antwoord.
Hieronder vindt u de implementatie van de recursieve benadering:
C++C// A Naive recursive implementation of LCS problem #include using namespace std; // Returns length of LCS for X[0..m-1], Y[0..n-1] int lcs(string X, string Y, int m, int n) // Driver code int main() { string S1 = 'AGGTAB'; string S2 = 'GXTXAYB'; int m = S1.size(); int n = S2.size(); cout << 'Length of LCS is ' << lcs(S1, S2, m, n); return 0; } // This code is contributed by rathbhupendra>Java// A Naive recursive implementation // of LCS problem #include int max(int a, int b); // Returns length of LCS for X[0..m-1], // Y[0..n-1] int lcs(char* X, char* Y, int i, int j) // Utility function to get max of // 2 integers int max(int a, int b) { return (a>B) ? a: b; } // Stuurprogrammacode int main() { char S1[] = 'BD'; char S2[] = 'ABCD'; int m = strlen(S1); int n = strlen(S2); int ik = 0, j = 0; // Functieaanroep printf('Lengte van LCS is%d', lcs(S1, S2, i, j)); retour 0; }>Python// A Naive recursive implementation of LCS problem in java import java.io.*; import java.util.*; public class LongestCommonSubsequence { // Returns length of LCS for X[0..m-1], Y[0..n-1] int lcs(String X, String Y, int m, int n) n == 0) return 0; if (X.charAt(m - 1) == Y.charAt(n - 1)) return 1 + lcs(X, Y, m - 1, n - 1); else return max(lcs(X, Y, m, n - 1), lcs(X, Y, m - 1, n)); // Utility function to get max of 2 integers int max(int a, int b) { return (a>B) ? a: b; } // Stuurprogrammacode public static void main(String[] args) { LongestCommonSubsequence lcs = new LongestCommonSubsequence(); Tekenreeks S1 = 'AGGTAB'; Tekenreeks S2 = 'GXTXAYB'; int m = S1.lengte(); int n = S2.lengte(); System.out.println('Lengte van LCS is' + ' ' + lcs.lcs(S1, S2, m, n)); } } // Deze code is bijgedragen door Saket Kumar>C## A Naive recursive Python implementation of LCS problem def lcs(X, Y, m, n): if m == 0 or n == 0: return 0 elif X[m-1] == Y[n-1]: return 1 + lcs(X, Y, m-1, n-1) else: return max(lcs(X, Y, m, n-1), lcs(X, Y, m-1, n)) # Driver code if __name__ == '__main__': S1 = 'AGGTAB' S2 = 'GXTXAYB' print('Length of LCS is', lcs(S1, S2, len(S1), len(S2)))>Javascript// C# Naive recursive implementation of LCS problem using System; class GFG { // Returns length of LCS for X[0..m-1], Y[0..n-1] static int lcs(String X, String Y, int m, int n) if (m == 0 // Utility function to get max of 2 integers static int max(int a, int b) { return (a>B) ? a: b; } // Stuurprogrammacode public static void Main() { String S1 = 'AGGTAB'; Tekenreeks S2 = 'GXTXAYB'; int m = S1.Lengte; int n = S2.Lengte; Console.Write('Lengte van LCS is' + ' ' + lcs(S1, S2, m, n)); } } // Deze code is bijgedragen door Sam007>PHP>
UitvoerLength of LCS is 4>Tijdcomplexiteit: O(2m+n)
Hulpruimte: O(1)Langste gemeenschappelijke subreeks (LCS) gebruikt Memoriseren :
1. Optimale onderbouw:
Voor het oplossen van de structuur van L(X[0, 1, . ., m-1], Y[0, 1, . . , n-1]) gebruiken we de hulp van de substructuren van X[0 , 1, …, m-2], Y[0, 1,…, n-2], afhankelijk van de situatie (dus optimaal gebruiken) om de oplossing van het geheel te vinden.
2. Overlappende deelproblemen:
Als we de bovenstaande recursieve benadering voor tekenreeksen gebruiken BD En ABCD , krijgen we een gedeeltelijke recursieboom zoals hieronder weergegeven. Hier kunnen we zien dat het deelprobleem L(BD, ABCD) meer dan eens wordt berekend. Als de totale boom in ogenschouw wordt genomen, zullen er meerdere van dergelijke overlappende deelproblemen zijn.
L(AXYT, AYZX)
/
L(AXY, AYZX) L(AXYT, AYZ)
/ /
L(AX, AYZX) L(AXY, AYZ) L(AXY, AYZ) L(AXYT, AY)Benadering: Vanwege de aanwezigheid van deze twee eigenschappen kunnen we dynamisch programmeren of onthouden gebruiken om het probleem op te lossen. Hieronder ziet u de aanpak voor de oplossing met behulp van recursie.
- Maak een recursieve functie. Maak ook een 2D-array om het resultaat van een unieke status op te slaan.
- Als dezelfde status tijdens de recursieoproep meerdere keren wordt aangeroepen, kunnen we direct het voor die status opgeslagen antwoord retourneren in plaats van opnieuw te berekenen.
Hieronder vindt u de implementatie van de bovenstaande aanpak:
C++Java// A Top-Down DP implementation // of LCS problem #include using namespace std; // Returns length of LCS for X[0..m-1], // Y[0..n-1] int lcs(char* X, char* Y, int m, int n, vector>& dp) { als (m == 0 || n == 0) retourneert 0; als (X[m - 1] == Y[n - 1]) retourneert dp[m][n] = 1 + lcs(X, Y, m - 1, n - 1, dp); als (dp[m][n] != -1) { return dp[m][n]; } return dp[m][n] = max(lcs(X, Y, m, n - 1, dp), lcs(X, Y, m - 1, n, dp)); } // Stuurprogrammacode int main() { char X[] = 'AGGTAB'; char Y[] = 'GXTXAYB'; int m = strlen(X); int n = strlen(Y); vector > dp(m + 1, vector (n+1, -1)); uit<< 'Length of LCS is ' << lcs(X, Y, m, n, dp); return 0; }> Python/*package whatever //do not write package name here */ import java.io.*; class GFG { // A Top-Down DP implementation of LCS problem // Returns length of LCS for X[0..m-1], Y[0..n-1] static int lcs(String X, String Y, int m, int n, int[][] dp) { if (m == 0 || n == 0) return 0; if (dp[m][n] != -1) return dp[m][n]; if (X.charAt(m - 1) == Y.charAt(n - 1)) { dp[m][n] = 1 + lcs(X, Y, m - 1, n - 1, dp); return dp[m][n]; } dp[m][n] = Math.max(lcs(X, Y, m, n - 1, dp), lcs(X, Y, m - 1, n, dp)); return dp[m][n]; } // Drivers code public static void main(String args[]) { String X = 'AGGTAB'; String Y = 'GXTXAYB'; int m = X.length(); int n = Y.length(); int[][] dp = new int[m + 1][n + 1]; for (int i = 0; i < m + 1; i++) { for (int j = 0; j < n + 1; j++) { dp[i][j] = -1; } } System.out.println('Length of LCS is ' + lcs(X, Y, m, n, dp)); } } // This code is contributed by shinjanpatra>C## A Top-Down DP implementation of LCS problem # Returns length of LCS for X[0..m-1], Y[0..n-1] def lcs(X, Y, m, n, dp): if (m == 0 or n == 0): return 0 if (dp[m][n] != -1): return dp[m][n] if X[m - 1] == Y[n - 1]: dp[m][n] = 1 + lcs(X, Y, m - 1, n - 1, dp) return dp[m][n] dp[m][n] = max(lcs(X, Y, m, n - 1, dp), lcs(X, Y, m - 1, n, dp)) return dp[m][n] # Driver code X = 'AGGTAB' Y = 'GXTXAYB' m = len(X) n = len(Y) dp = [[-1 for i in range(n + 1)]for j in range(m + 1)] print(f'Length of LCS is {lcs(X, Y, m, n, dp)}') # This code is contributed by shinjanpatra>Javascript/* C# Naive recursive implementation of LCS problem */ using System; class GFG { /* Returns length of LCS for X[0..m-1], Y[0..n-1] */ static int lcs(char[] X, char[] Y, int m, int n, int[, ] L) { if (m == 0 || n == 0) return 0; if (L[m, n] != -1) return L[m, n]; if (X[m - 1] == Y[n - 1]) { L[m, n] = 1 + lcs(X, Y, m - 1, n - 1, L); return L[m, n]; } L[m, n] = max(lcs(X, Y, m, n - 1, L), lcs(X, Y, m - 1, n, L)); return L[m, n]; } /* Utility function to get max of 2 integers */ static int max(int a, int b) { return (a>B) ? a: b; } public static void Main() { String s1 = 'AGGTAB'; Tekenreeks s2 = 'GXTXAYB'; char[] X = s1.ToCharArray(); char[] Y = s2.ToCharArray(); int m = X.Lengte; int n = Y.Lengte; int[, ] L = nieuwe int[m + 1, n + 1]; voor (int i = 0; ik<= m; i++) { for (int j = 0; j <= n; j++) { L[i, j] = -1; } } Console.Write('Length of LCS is' + ' ' + lcs(X, Y, m, n, L)); } } // This code is contributed by akshitsaxenaa09>/* A Top-Down DP implementation of LCS problem */ /* Returns length of LCS for X[0..m-1], Y[0..n-1] */ function lcs(X, Y, m, n, dp) { if (m == 0 || n == 0) return 0; if (X[m - 1] == Y[n - 1]) return dp[m][n] = 1 + lcs(X, Y, m - 1, n - 1, dp); if (dp[m][n] != -1) { return dp[m][n]; } return dp[m][n] = Math.max(lcs(X, Y, m, n - 1, dp), lcs(X, Y, m - 1, n, dp)); } /* Driver code */ let X = 'AGGTAB'; let Y = 'GXTXAYB'; let m = X.length; let n = Y.length; let dp = new Array(m + 1); for(let i = 0; i < m + 1; i++) { dp[i] = new Array(n + 1).fill(-1); } console.log('Length of LCS is ' + lcs(X, Y, m, n, dp)); // This code is contributed by shinjanpatra>
UitvoerLength of LCS is 4>Tijdcomplexiteit: O(m * n) waarbij m en n de snaarlengtes zijn.
Hulpruimte: O(m * n) Hier wordt de recursieve stapelruimte genegeerd.Langste gemeenschappelijke subreeks (LCS) met behulp van bottom-up (tabellering):
We kunnen de volgende stappen gebruiken om de dynamische programmeeraanpak voor LCS te implementeren.
json van Java-object
- Maak een 2D-array dp[][] met rijen en kolommen gelijk aan de lengte van elke invoerreeks plus 1 [het aantal rijen geeft de indices aan van S1 en de kolommen geven de indices aan van S2 ].
- Initialiseer de eerste rij en kolom van de dp-array naar 0.
- Herhaal de rijen van de dp-array, beginnend bij 1 (bijvoorbeeld met behulp van iterator i ).
- Voor elk i , itereer alle kolommen van j = 1 tot n :
- Als S1[i-1] is gelijk aan S2[j-1] , stel het huidige element van de dp-array in op de waarde van het element ( dp[i-1][j-1] + 1 ).
- Stel anders het huidige element van de dp-array in op de maximale waarde van dp[i-1][j] En dp[i][j-1] .
- Na de geneste lussen bevat het laatste element van de dp-array de lengte van de LCS.
Zie de onderstaande afbeelding voor een beter begrip:
Illustratie:
Zeg dat de snaren dat zijn S1 = AGGTAB En S2 = GXTXAYB .
Eerste stap: Maak in eerste instantie een 2D-matrix (zeg dp[][]) met de grootte 8 x 7, waarvan de eerste rij en eerste kolom zijn gevuld met 0.
Het maken van de dp-tabel
Tweede stap: Beweeg voor i = 1. Wanneer j 5 wordt, zijn S1[0] en S2[4] gelijk. Dus de dp[][] is bijgewerkt. Voor de overige elementen geldt het maximum van dp[i-1][j] en dp[i][j-1]. (In dit geval, als beide waarden gelijk zijn, hebben we pijlen naar de vorige rijen gebruikt).
Het invullen van rij nr. 1
Derde stap: Hoewel ze worden doorlopen voor i = 2, zijn S1[1] en S2[0] hetzelfde (beide zijn ‘G’). De dp-waarde in die cel wordt dus bijgewerkt. De overige elementen worden bijgewerkt volgens de voorwaarden.
Het invullen van rij nr. 2
Vierde stap: Voor i = 3 zijn S1[2] en S2[0] opnieuw hetzelfde. De updates zijn als volgt.
Vulrij nr. 3
Vijfde stap: Voor i = 4 kunnen we zien dat S1[3] en S2[2] hetzelfde zijn. Dus dp[4][3] bijgewerkt als dp[3][2] + 1 = 2.
Vulrij 4
Zesde stap: Hier kunnen we zien dat voor i = 5 en j = 5 de waarden van S1[4] en S2[4] hetzelfde zijn (dat wil zeggen, beide zijn ‘A’). Dus dp[5][5] wordt dienovereenkomstig bijgewerkt en wordt 3.
Vulrij 5
Laatste stap: Voor i = 6: zie dat de laatste tekens van beide strings hetzelfde zijn (ze zijn ‘B’). Daarom wordt de waarde van dp[6][7] 4.
Het vullen van de laatste rij
We krijgen dus de maximale lengte van een gemeenschappelijke deelreeks als 4 .
Hieronder volgt een tabel met een implementatie voor het LCS-probleem.
maat lettertype latexC++Java// Dynamic Programming C++ implementation // of LCS problem #include using namespace std; // Returns length of LCS for X[0..m-1], // Y[0..n-1] int lcs(string X, string Y, int m, int n) { // Initializing a matrix of size // (m+1)*(n+1) int L[m + 1][n + 1]; // Following steps build L[m+1][n+1] // in bottom up fashion. Note that // L[i][j] contains length of LCS of // X[0..i-1] and Y[0..j-1] for (int i = 0; i <= m; i++) { for (int j = 0; j <= n; j++) if (i == 0 } // L[m][n] contains length of LCS // for X[0..n-1] and Y[0..m-1] return L[m][n]; } // Driver code int main() { string S1 = 'AGGTAB'; string S2 = 'GXTXAYB'; int m = S1.size(); int n = S2.size(); // Function call cout << 'Length of LCS is ' << lcs(S1, S2, m, n); return 0; }>Python// Dynamic Programming Java implementation of LCS problem import java.util.*; public class LongestCommonSubsequence { // Returns length of LCS for X[0..m-1], Y[0..n-1] int lcs(String X, String Y, int m, int n) { int L[][] = new int[m + 1][n + 1]; // Following steps build L[m+1][n+1] in bottom up // fashion. Note that L[i][j] contains length of LCS // of X[0..i-1] and Y[0..j-1] for (int i = 0; i <= m; i++) { for (int j = 0; j <= n; j++) j == 0) L[i][j] = 0; else if (X.charAt(i - 1) == Y.charAt(j - 1)) L[i][j] = L[i - 1][j - 1] + 1; else L[i][j] = max(L[i - 1][j], L[i][j - 1]); } return L[m][n]; } // Utility function to get max of 2 integers int max(int a, int b) { return (a>B) ? a: b; } public static void main(String[] args) {LongestCommonSubsequence lcs = new LongestCommonSubsequence(); Tekenreeks S1 = 'AGGTAB'; Tekenreeks S2 = 'GXTXAYB'; int m = S1.lengte(); int n = S2.lengte(); System.out.println('Lengte van LCS is' + ' ' + lcs.lcs(S1, S2, m, n)); } } // Deze code is bijgedragen door Saket Kumar>C## Dynamic Programming implementation of LCS problem def lcs(X, Y, m, n): # Declaring the array for storing the dp values L = [[None]*(n+1) for i in range(m+1)] # Following steps build L[m+1][n+1] in bottom up fashion # Note: L[i][j] contains length of LCS of X[0..i-1] # and Y[0..j-1] for i in range(m+1): for j in range(n+1): if i == 0 or j == 0: L[i][j] = 0 elif X[i-1] == Y[j-1]: L[i][j] = L[i-1][j-1]+1 else: L[i][j] = max(L[i-1][j], L[i][j-1]) # L[m][n] contains the length of LCS of X[0..n-1] & Y[0..m-1] return L[m][n] # Driver code if __name__ == '__main__': S1 = 'AGGTAB' S2 = 'GXTXAYB' m = len(S1) n = len(S2) print('Length of LCS is', lcs(S1, S2, m, n)) # This code is contributed by Nikhil Kumar Singh(nickzuck_007)>Javascript// Dynamic Programming implementation of LCS problem using System; class GFG { // Returns length of LCS for X[0..m-1], Y[0..n-1] static int lcs(String X, String Y, int m, int n) { int[, ] L = new int[m + 1, n + 1]; // Following steps build L[m+1][n+1] // in bottom up fashion. // Note that L[i][j] contains length of // LCS of X[0..i-1] and Y[0..j-1] for (int i = 0; i <= m; i++) { for (int j = 0; j <= n; j++) j == 0) L[i, j] = 0; else if (X[i - 1] == Y[j - 1]) L[i, j] = L[i - 1, j - 1] + 1; else L[i, j] = max(L[i - 1, j], L[i, j - 1]); } return L[m, n]; } // Utility function to get max of 2 integers static int max(int a, int b) { return (a>B) ? a: b; } // Stuurprogrammacode public static void Main() { String S1 = 'AGGTAB'; Tekenreeks S2 = 'GXTXAYB'; int m = S1.Lengte; int n = S2.Lengte; Console.Write('Lengte van LCS is' + ' ' + lcs(S1, S2, m, n)); } } // Deze code is bijgedragen door Sam007>PHP// Dynamic Programming Java implementation of LCS problem // Utility function to get max of 2 integers function max(a, b) { if (a>b) retourneer a; anders terug b; } // Retourneert de lengte van LCS voor X[0..m-1], Y[0..n-1] functie lcs(X, Y, m, n) { var L = new Array(m + 1); for(var i = 0; ik< L.length; i++) { L[i] = new Array(n + 1); } var i, j; /* Following steps build L[m+1][n+1] in bottom up fashion. Note that L[i][j] contains length of LCS of X[0..i-1] and Y[0..j-1] */ for(i = 0; i <= m; i++) { for(j = 0; j <= n; j++) j == 0) L[i][j] = 0; else if (X[i - 1] == Y[j - 1]) L[i][j] = L[i - 1][j - 1] + 1; else L[i][j] = max(L[i - 1][j], L[i][j - 1]); } /* L[m][n] contains length of LCS for X[0..n-1] and Y[0..m-1] */ return L[m][n]; } // Driver code var S1 = 'AGGTAB'; var S2 = 'GXTXAYB'; var m = S1.length; var n = S2.length; console.log('Length of LCS is ' + lcs(S1, S2, m, n)); // This code is contributed by akshitsaxenaa09>// Dynamic Programming C# // implementation of LCS problem function lcs($X , $Y, $m, $n) { // Following steps build L[m+1][n+1] // in bottom up fashion . // Note: L[i][j] contains length of // LCS of X[0..i-1] and Y[0..j-1] for ($i = 0; $i <= $m; $i++) { for ($j = 0; $j <= $n; $j++) if ($i == 0 } // L[m][n] contains the length of // LCS of X[0..n-1] & Y[0..m-1] return $L[$m][$n]; } // Driver Code $S1 = 'AGGTAB'; $S2 = 'GXTXAYB'; $m = strlen($S1); $n = strlen($S2) ; echo 'Length of LCS is '; echo lcs($S1, $S2, $m, $n); // This code is contributed // by Shivi_Aggarwal ?>>
UitvoerLength of LCS is 4>Tijdcomplexiteit: O(m * n), wat veel beter is dan de tijdscomplexiteit in het slechtste geval van de naïeve recursieve implementatie.
Hulpruimte: O(m * n) omdat het algoritme een array van grootte (m+1)*(n+1) gebruikt om de lengte van de gemeenschappelijke substrings op te slaan.Langste gemeenschappelijke subreeks (LCS) met behulp van bottom-up (ruimte-optimalisatie):
- In de bovenstaande tabelleringsbenadering gebruiken we L[i-1][j] en L[i][j] enz., hier verwijst de L[i-1] naar de vorige rij van de matrix L en verwijst L[i] naar de huidige rij.
- We kunnen ruimte-optimalisatie uitvoeren door twee vectoren te gebruiken, de ene is de vorige en de andere is de huidige.
- Wanneer de binnenste for-lus verlaat, initialiseren we de vorige gelijk aan de huidige.
Hieronder vindt u de implementatie:
C++Java// Dynamic Programming C++ implementation // of LCS problem #include using namespace std; int longestCommonSubsequence(string& text1, string& text2) { int n = text1.size(); int m = text2.size(); // initializing 2 vectors of size m vectorvorige(m + 1, 0), cur(m + 1, 0); voor (int idx2 = 0; idx2< m + 1; idx2++) cur[idx2] = 0; for (int idx1 = 1; idx1 < n + 1; idx1++) { for (int idx2 = 1; idx2 < m + 1; idx2++) { // if matching if (text1[idx1 - 1] == text2[idx2 - 1]) cur[idx2] = 1 + prev[idx2 - 1]; // not matching else cur[idx2] = 0 + max(cur[idx2 - 1], prev[idx2]); } prev = cur; } return cur[m]; } int main() { string S1 = 'AGGTAB'; string S2 = 'GXTXAYB'; // Function call cout << 'Length of LCS is ' << longestCommonSubsequence(S1, S2); return 0; }> Python// Dynamic Programming Java implementation of LCS problem import java.util.Arrays; public class GFG { public static int longestCommonSubsequence(String text1, String text2) { int n = text1.length(); int m = text2.length(); // Initializing 2 arrays of size m int[] prev = new int[m + 1]; int[] cur = new int[m + 1]; for (int idx1 = 1; idx1 < n + 1; idx1++) { for (int idx2 = 1; idx2 < m + 1; idx2++) { // If matching if (text1.charAt(idx1 - 1) == text2.charAt(idx2 - 1)) cur[idx2] = 1 + prev[idx2 - 1]; // Not matching else cur[idx2] = Math.max(cur[idx2 - 1], prev[idx2]); } prev = Arrays.copyOf(cur, m + 1); } return cur[m]; } public static void main(String[] args) { String S1 = 'AGGTAB'; String S2 = 'GXTXAYB'; // Function call System.out.println('Length of LCS is ' + longestCommonSubsequence(S1, S2)); } }>C#def longestCommonSubsequence(text1, text2): n = len(text1) m = len(text2) # Initializing two lists of size m prev = [0] * (m + 1) cur = [0] * (m + 1) for idx1 in range(1, n + 1): for idx2 in range(1, m + 1): # If characters are matching if text1[idx1 - 1] == text2[idx2 - 1]: cur[idx2] = 1 + prev[idx2 - 1] else: # If characters are not matching cur[idx2] = max(cur[idx2 - 1], prev[idx2]) prev = cur.copy() return cur[m] if __name__ == '__main__': S1 = 'AGGTAB' S2 = 'GXTXAYB' # Function call print('Length of LCS is', longestCommonSubsequence(S1, S2)) # This code is contributed by Rishabh Mathur>Javascriptusing System; class Program { static int LongestCommonSubsequence(string text1, string text2) { int n = text1.Length; int m = text2.Length; // initializing 2 arrays of size m int[] prev = new int[m + 1]; int[] cur = new int[m + 1]; for (int idx2 = 0; idx2 < m + 1; idx2++) cur[idx2] = 0; for (int idx1 = 1; idx1 < n + 1; idx1++) { for (int idx2 = 1; idx2 < m + 1; idx2++) { // if matching if (text1[idx1 - 1] == text2[idx2 - 1]) cur[idx2] = 1 + prev[idx2 - 1]; // not matching else cur[idx2] = 0 + Math.Max(cur[idx2 - 1], prev[idx2]); } prev = cur; } return cur[m]; } static void Main() { string S1 = 'AGGTAB'; string S2 = 'GXTXAYB'; // Function call Console.WriteLine('Length of LCS is ' + LongestCommonSubsequence(S1, S2)); } }>function longestCommonSubsequence(text1, text2) { const n = text1.length; const m = text2.length; // Initializing two arrays of size m let prev = new Array(m + 1).fill(0); let cur = new Array(m + 1).fill(0); for (let idx2 = 0; idx2 < m + 1; idx2++) { cur[idx2] = 0; } for (let idx1 = 1; idx1 < n + 1; idx1++) { for (let idx2 = 1; idx2 < m + 1; idx2++) { // If characters match if (text1[idx1 - 1] === text2[idx2 - 1]) { cur[idx2] = 1 + prev[idx2 - 1]; } // If characters don't match else { cur[idx2] = Math.max(cur[idx2 - 1], prev[idx2]); } } // Update the 'prev' array prev = [...cur]; } return cur[m]; } // Main function function main() { const S1 = 'AGGTAB'; const S2 = 'GXTXAYB'; // Function call console.log('Length of LCS is ' + longestCommonSubsequence(S1, S2)); } // Call the main function main();>
UitvoerLength of LCS is 4>Tijdcomplexiteit: O(m * n), wat hetzelfde blijft.
Hulpruimte: O(m) omdat het algoritme twee arrays met de grootte m gebruikt.







