Logistieke regressie in R-programmering is een classificatiealgoritme dat wordt gebruikt om de waarschijnlijkheid van het succes en het mislukken van gebeurtenissen te bepalen. Logistieke regressie wordt gebruikt wanneer de afhankelijke variabele binair (0/1, Waar/Onwaar, Ja/Nee) van aard is. De logitfunctie wordt gebruikt als linkfunctie in een binominale verdeling.
De waarschijnlijkheid van een binaire uitkomstvariabele kan worden voorspeld met behulp van de statistische modelleringstechniek die bekend staat als logistische regressie. Het wordt op grote schaal gebruikt in veel verschillende industrieën, waaronder marketing, financiën, sociale wetenschappen en medisch onderzoek.
De logistieke functie, gewoonlijk de sigmoïdefunctie genoemd, is het basisidee dat ten grondslag ligt aan logistieke regressie. Deze sigmoïdefunctie wordt gebruikt bij logistische regressie om de correlatie tussen de voorspellende variabelen en de waarschijnlijkheid van de binaire uitkomst te beschrijven.

Logistieke regressie in R-programmering
Logistieke regressie wordt ook wel genoemd Binomiale logistieke regressie . Het is gebaseerd op de sigmoïdefunctie waarbij de uitvoer de waarschijnlijkheid is en de invoer van -oneindig tot +oneindig kan zijn.
Theorie
Logistieke regressie wordt ook wel een gegeneraliseerd lineair model genoemd. Omdat het wordt gebruikt als classificatietechniek om een kwalitatief antwoord te voorspellen, varieert de waarde van y van 0 tot 1 en kan deze worden weergegeven door de volgende vergelijking:

Logistieke regressie in R-programmering
P is de waarschijnlijkheid van een kenmerk van interesse. De odds ratio wordt gedefinieerd als de kans op succes in vergelijking met de kans op falen. Het is een belangrijke weergave van logistieke regressiecoëfficiënten en kan waarden aannemen tussen 0 en oneindig. De odds ratio van 1 is wanneer de kans op succes gelijk is aan de kans op mislukking. De odds ratio van 2 is wanneer de kans op succes tweemaal zo groot is als de kans op falen. De odds ratio van 0,5 is wanneer de kans op falen tweemaal zo groot is als de kans op succes.
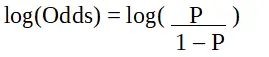
Logistieke regressie in R-programmering
Omdat we met een binomiale verdeling (afhankelijke variabele) werken, moeten we een linkfunctie kiezen die het meest geschikt is voor deze verdeling.
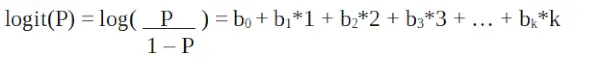
Logistieke regressie in R-programmering
Het is een logit-functie . In de bovenstaande vergelijking is het haakje gekozen om de waarschijnlijkheid van het waarnemen van de steekproefwaarden te maximaliseren in plaats van de som van de kwadratische fouten te minimaliseren (zoals bij gewone regressie). De logit wordt ook wel een log of odds genoemd. De logitfunctie moet lineair gerelateerd zijn aan de onafhankelijke variabelen. Dit komt uit vergelijking A, waarbij de linkerkant een lineaire combinatie van x is. Dit is vergelijkbaar met de OLS-aanname dat y lineair gerelateerd is aan x. Variabelen b0, b1, b2 … enz. zijn onbekend en moeten worden geschat op basis van beschikbare trainingsgegevens. In een logistisch regressiemodel verandert het vermenigvuldigen van b1 met één eenheid de logit met b0. De P-veranderingen als gevolg van een verandering van één eenheid zijn afhankelijk van de vermenigvuldigde waarde. Als b1 positief is, zal P toenemen en als b1 negatief is, zal P afnemen.
De gegevensset
mtcars (motor trend car road test) omvat brandstofverbruik, prestaties en 10 aspecten van auto-ontwerp voor 32 auto's. Het wordt vooraf geïnstalleerd geleverd dplyr pakket in r.
R
1 miljoen nummer
# Installing the package> install.packages>(>'dplyr'>)> # Loading package> library>(dplyr)> # Summary of dataset in package> summary>(mtcars)> |
>
>
Logistieke regressie uitvoeren op een dataset
Logistieke regressie wordt geïmplementeerd in R met behulp van glm() door het model te trainen met behulp van functies of variabelen in de dataset.
R
# Installing the package> # For Logistic regression> install.packages>(>'caTools'>)> # For ROC curve to evaluate model> install.packages>(>'ROCR'>)> > # Loading package> library>(caTools)> library>(ROCR)> |
>
>
Het splitsen van de gegevens
R
# Splitting dataset> split <->sample.split>(mtcars, SplitRatio = 0.8)> split> train_reg <->subset>(mtcars, split ==>'TRUE'>)> test_reg <->subset>(mtcars, split ==>'FALSE'>)> # Training model> logistic_model <->glm>(vs ~ wt + disp,> >data = train_reg,> >family =>'binomial'>)> logistic_model> # Summary> summary>(logistic_model)> |
>
>
Uitgang:
Call: glm(formula = vs ~ wt + disp, family = 'binomial', data = train_reg) Deviance Residuals: Min 1Q Median 3Q Max -1.6552 -0.4051 0.4446 0.6180 1.9191 Coefficients: Estimate Std. Error z value Pr(>|z|) (Interceptie) 1,58781 2,60087 0,610 0,5415 wt 1,36958 1,60524 0,853 0,3936 disp -0,02969 0,01577 -1,882 0,0598 . --- Betekenis. codes: 0 '***' 0,001 '**' 0,01 '*' 0,05 '.' 0,1 ' ' 1 (Dispersieparameter voor binominale familie wordt als 1 beschouwd) Nulafwijking: 34,617 op 24 vrijheidsgraden Residuele afwijking: 20,212 op 22 vrijheidsgraden AIC: 26.212 Aantal Fisher Scoring-iteraties: 6>
- Oproep: de functieaanroep die wordt gebruikt om in het logistische regressiemodel te passen, wordt weergegeven, samen met informatie over de familie, formule en gegevens. Deviantieresiduen: Dit zijn de deviantieresiduen, die de mate van goodness-of-fit van het model meten. Ze duiden op discrepanties tussen feitelijke reacties en de waarschijnlijkheid voorspeld door het logistische regressiemodel. Coëfficiënten: Deze coëfficiënten in logistische regressie vertegenwoordigen de log odds of logit van de responsvariabele. De standaardfouten gerelateerd aan de geschatte coëfficiënten worden weergegeven in de Std. Foutkolom. Significantiecodes: Het significantieniveau van elke voorspellende variabele wordt aangegeven door de significantiecodes. Dispersieparameter: Bij logistische regressie dient de dispersieparameter als schaalparameter voor de binominale verdeling. In dit geval is deze ingesteld op 1, wat aangeeft dat de veronderstelde spreiding 1 is. Nulafwijking: De nulafwijking berekent de afwijking van het model wanneer alleen rekening wordt gehouden met het snijpunt. Het symboliseert de afwijking die zou voortvloeien uit een model zonder voorspellers. Residuele afwijking: De resterende afwijking berekent de afwijking van het model nadat de voorspellers zijn aangepast. Het staat voor de resterende afwijking nadat rekening is gehouden met de voorspellers. AIC: Het Akaike Information Criterion (AIC), dat rekening houdt met het aantal voorspellers, is een maatstaf voor de geschiktheid van een model. Het bestraft meer ingewikkelde modellen om overfitting te voorkomen. Beter passende modellen worden aangegeven door lagere AIC-waarden. Aantal Fisher Scoring-iteraties: Het aantal iteraties dat nodig is voor de Fisher-scoreprocedure om de modelparameters te schatten, wordt aangegeven door het aantal iteraties.
Voorspel testgegevens op basis van model
R
microservices-tutorial
predict_reg <->predict>(logistic_model,> >test_reg, type =>'response'>)> predict_reg> |
>
>
Uitgang:
Hornet Sportabout Merc 280C Merc 450SE Chrysler Imperial 0.01226166 0.78972164 0.26380531 0.01544309 AMC Javelin Camaro Z28 Ford Pantera L 0.06104267 0.02807992 0.01107943>
R
# Changing probabilities> predict_reg <->ifelse>(predict_reg>0,5, 1, 0)> # Evaluating model accuracy> # using confusion matrix> table>(test_reg$vs, predict_reg)> missing_classerr <->mean>(predict_reg != test_reg$vs)> print>(>paste>(>'Accuracy ='>, 1 - missing_classerr))> # ROC-AUC Curve> ROCPred <->prediction>(predict_reg, test_reg$vs)> ROCPer <->performance>(ROCPred, measure =>'tpr'>,> >x.measure =>'fpr'>)> auc <->performance>(ROCPred, measure =>'auc'>)> auc <- [email protected][[1]]> auc> # Plotting curve> plot>(ROCPer)> plot>(ROCPer, colorize =>TRUE>,> >print.cutoffs.at =>seq>(0.1, by = 0.1),> >main =>'ROC CURVE'>)> abline>(a = 0, b = 1)> auc <->round>(auc, 4)> legend>(.6, .4, auc, title =>'AUC'>, cex = 1)> |
>
>
Uitgang:
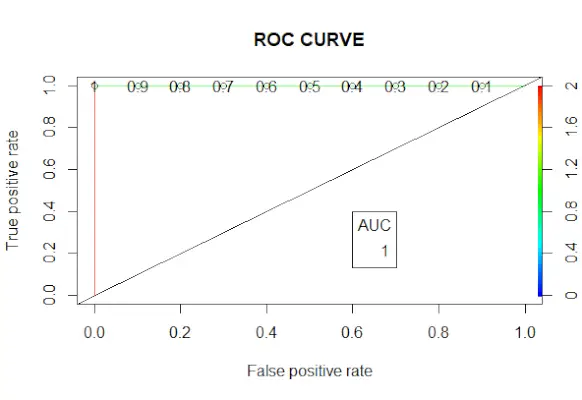
ROC-curve
Voorbeeld 2:
We kunnen een logistisch regressiemodel uitvoeren Titanic Data set in R.
R
# Load the dataset> data>(Titanic)> # Convert the table to a data frame> data <->as.data.frame>(Titanic)> # Fit the logistic regression model> model <->glm>(Survived ~ Class + Sex + Age, family = binomial, data = data)> # View the summary of the model> summary>(model)> |
>
>
Uitgang:
Call: glm(formula = Survived ~ Class + Sex + Age, family = binomial, data = data) Deviance Residuals: Min 1Q Median 3Q Max -1.177 -1.177 0.000 1.177 1.177 Coefficients: Estimate Std. Error z value Pr(>|z|) (Onderschepping) 4.022e-16 8.660e-01 0 1 Klasse2e -9.762e-16 1.000e+00 0 1 Klasse3e -4.699e-16 1.000e+00 0 1 KlasseBemanning -5.551e-16 1.000e+ 00 0 1 GeslachtVrouw -3.140e-16 7.071e-01 0 1 LeeftijdVolwassene 5.103e-16 7.071e-01 0 1 (Verspreidingsparameter voor binomiale familie is 1) Nulafwijking: 44.361 op 31 vrijheidsgraden Residuele afwijking: 44.361 op 26 vrijheidsgraden AIC: 56.361 Aantal Fisher Scoring-iteraties: 2>
Teken de ROC-curve voor de Titanic-gegevensset
R
# Install and load the required packages> install.packages>(>'ROCR'>)> library>(ROCR)> # Fit the logistic regression model> model <->glm>(Survived ~ Class + Sex + Age, family = binomial, data = data)> # Make predictions on the dataset> predictions <->predict>(model, type =>'response'>)> # Create a prediction object for ROCR> prediction_objects <->prediction>(predictions, titanic_df$Survived)> # Create an ROC curve object> roc_object <->performance>(prediction_obj, measure =>'tpr'>, x.measure =>'fpr'>)> # Plot the ROC curve> plot>(roc_object, main =>'ROC Curve'>, col =>'blue'>, lwd = 2)> # Add labels and a legend to the plot> legend>(>'bottomright'>, legend => >paste>(>'AUC ='>,>round>(>performance>(prediction_objects, measure =>'auc'>)> >@y.values[[1]], 2)), col =>'blue'>, lwd = 2)> |
tijger leeuw verschil
>
>
Uitgang:
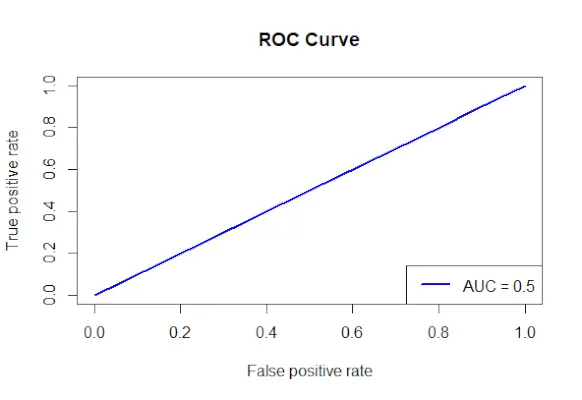
ROC-curve
- De factoren die worden gebruikt om Overleefd te voorspellen zijn gespecificeerd, en de formule Overleefde klasse + Geslacht + Leeftijd wordt gebruikt om een logistisch regressiemodel te creëren.
- Met behulp van de functie voorspellen() worden voorspellingen gedaan over de dataset met behulp van het aangepaste model.
- De geprojecteerde kansen worden gecombineerd met de werkelijke uitkomstwaarden om een voorspellingsobject te bouwen met behulp van de voorspelling() methode uit het ROCR-pakket.
- De maatstaf van de werkelijk positieve snelheid (tpr) en de x-asmaat van de vals-positieve snelheid (fpr) worden gespecificeerd, en er wordt een ROC-curveobject gemaakt met behulp van de functie performance() uit het ROCR-pakket.
- Het ROC-curveobject (roc_obj), dat de hoofdtitel, kleur en lijndikte specificeert, wordt geplot met behulp van de functie plot().
- Het gebruikt de functie performance() met Measure = auc om de AUC-waarde (gebied onder de curve) te bepalen en voegt labels en een legenda aan de plot toe.
