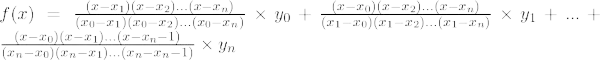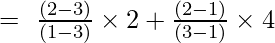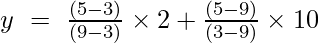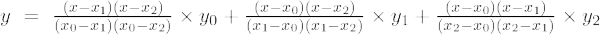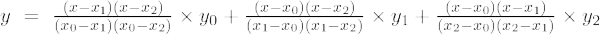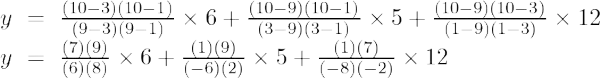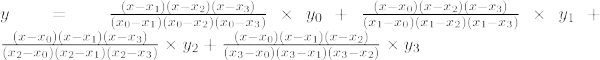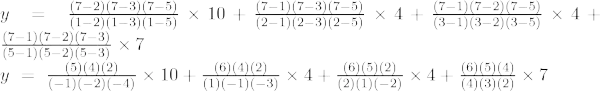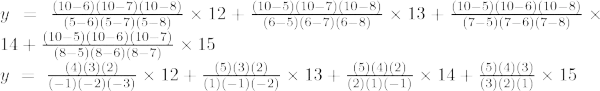logo

TechCodeview

Lagrange-interpolatieformule

Lagrange-interpolatieformule vindt een polynoom met de naam Lagrange-polynoom dat op een willekeurig punt bepaalde waarden aanneemt. Het is een n-de graad polynoomuitdrukking van de functie f(x). De interpolatiemethode wordt gebruikt om de nieuwe datapunten te vinden binnen het bereik van een discrete set bekende datapunten.

In dit artikel zullen we in detail leren over Lagrange-interpolatie, Lagrange-interpolatieformule, bewijs voor Lagrange-interpolatieformule, voorbeelden gebaseerd op Lagrange-interpolatieformule en andere.



Wat is Lagrange-interpolatie?

Lagrange-interpolatie is een manier om de waarde van een functie op een bepaald punt te vinden wanneer de functie niet is opgegeven. We gebruiken andere punten op de functie om de waarde van de functie op elk gewenst punt te bepalen.

Stel dat we een functie y = f(x) hebben waarin het vervangen van de waarden van x verschillende waarden van y oplevert. En we krijgen twee punten (x1, En1) en (x2, En2) op de curve, dan wordt de waarde van y bij x = a(constant) berekend met behulp van de Lagrange-interpolatieformule.

Lagrange-interpolatieformule

Gegeven enkele reële waarden x1, X2, X3, …, XNen j1, En2, En3, …, EnNen er zal een polynoom P zijn met reële coëfficiënten die voldoen aan de voorwaarden P(xi) = eni, ∀ i = {1, 2, 3, …, n} en de graad van polynoom P moet kleiner zijn dan het aantal reële waarden, dat wil zeggen graad (P)



Lagrange-interpolatieformule voor n-de volgorde

De Lagrange-interpolatieformule voor negradenpolynoom wordt hieronder gegeven:

Lagrange-interpolatieformule voor de n e bestelling is,

f(x)=frac{(x-x_1)(x-x_2)...(x-x_n)}{(x_0-x_1)(x_0-x_2)...(x_0-x_n)}maal y_0+ frac{(x-x_0)(x-x_2)...(x-x_n)}{(x_1-x_0)(x_1-x_2)...(x_1-x_n)} imes y_1+...+ frac{(x-x_0)(x-x_1)...(x-x_n-1)}{(x_n-x_0)(x_n-x_1)...(x_n-x_n-1)}maal y_n



Lagrange-interpolatieformule van de eerste orde

Als de De graad van de polynoom is 1 en wordt dan de eerste orde polynoom genoemd. Lagrange-interpolatieformule voor 1stordepolynomen is,

f(x)~=~frac{(x-x_1)}{(x_0-x_1)} ijden y_0+frac{(x-x_0)}{(x_1-x_0)} ijden y_1

Lagrange tweede orde interpolatieformule

Als de graad van het polynoom 2 is, wordt het tweede orde polynoom genoemd. Lagrange-interpolatieformule voor polynomen van de 2e orde is:

f(x)~=~frac{(x-x_1)(x-x_2)}{(x_0-x_1)(x_0-x_2)} imes y_0+frac{(x-x_0)(x-x_2)} {(x_1-x_0)(x_1-x_2)}maal y_1+frac{(x-x_0)(x-x_1)}{(x_2-x_0)(x_2-x_1)}maal y_2

Bewijs van de stelling van Lagrange

Laten we een polynoom van de gegeven vorm bekijken,

f(x) = A0(x-x1)(x – x2)(x – x3)…(x – xN) + EEN1(x-x1)(x – x2)(x – x3)…(x – xN) + … + A(n-1)(x-x1)(x – x2)(x – x3)…(x – xN)

Vervang observaties xiom A te krijgeni

Stel x = x0dan krijgen we A0

f(x0) = en0= EEN0(X0- X1)(X0- X2)(X0- X3)…(X0- XN)

A 0 = en 0 /(X 0 - X 1 )(X 0 - X 2 )(X 0 - X 3 )…(X 0 - X N )

Door x = x te vervangen1wij krijgen A1

f(x1) = en1= EEN1(X1- X0)(X1- X2)(X1- X3)…(X1- XN)

A 1 = en 1 /(X 1 - X 0 )(X 1 - X 2 )(X 1 - X 3 )…(X 1 - X N )

Op dezelfde manier, door x = x te vervangenNwij krijgen AN

f(xN) = enN= EENN(XN- X0)(XN- X1)(XN- X2)…(XN- Xn-1)

A N = en N /(X N - X 0 )(X N - X 1 )(X N - X 2 )…(X N - X n-1 )

Als we alle waarden van A vervangeniin functie f(x) waarbij i = 1, 2, 3, ...n dan krijgen we de Lagrange-interpolatieformule als,

hoe oud is pete davidson

f(x)~=~frac{(x-x_1)(x-x_2)...(x-x_n)}{(x_0-x_1)(x_0-x_2)...(x_0-x_n)} keer y_0+frac{(x-x_0)(x-x_2)...(x-x_n)}{(x_1-x_0)(x_1-x_2)...(x_1-x_n)} ijden y_1+... +frac{(x-x_0)(x-x_1)...(x-x_n-1)}{(x_n-x_0)(x_n-x_1)...(x_n-x_n-1)}maal y_n

Eigenschappen van Lagrange-interpolatieformule

Verschillende eigenschappen van de Lagrange-interpolatieformule worden hieronder besproken,

  • Deze formule wordt gebruikt om de waarde van de functie op elk moment te vinden, zelfs als de functie zelf niet is opgegeven.
  • Het wordt zelfs gebruikt als de gegeven punten niet gelijkmatig verdeeld zijn.
  • Het geeft de waarde van de afhankelijke variabele voor elke onafhankelijke variabele die tot een functie behoort en wordt dus gebruikt in numeraciale analyse voor het vinden van de waarden van de functie, enz.

Gebruik van Lagrange-interpolatieformule

Hieronder worden verschillende toepassingen van de Lagrange-interpolatieformule besproken,

  • Het wordt gebruikt om de waarde van de afhankelijke variabele bij een bepaalde onafhankelijke variabele te vinden, zelfs als de functie zelf niet is gegeven.
  • Het wordt gebruikt bij het schalen van afbeeldingen.
  • Het wordt gebruikt bij AI-modellering.
  • Het wordt gebruikt om NLP's te onderwijzen, enz.

Lees verder,

  • Interpolatieformule
  • Lineaire interpolatieformule

Voorbeelden waarbij de Lagrange-interpolatieformule wordt gebruikt

Laten we eens kijken naar enkele voorbeeldvragen over de Lagrange-interpolatieformule.

Voorbeeld 1: Vind de waarde van y bij x = 2 voor de gegeven reeks punten (1, 2),(3, 4)

Oplossing:

Gegeven,

  • (X0, En0) = (1, 2)
  • (X1, En1) = (3, 4)

De Lagrange-interpolatieformule van de eerste orde is:

y~=~frac{(x-x_1)}{(x_0-x_1)} ijden y_0+frac{(x-x_0)}{(x_1-x_0)} ijden y_1

Bij x = 2

En =~frac{(2-3)}{(1-3)} ijden 2+frac{(2-1)}{(3-1)} ijden 4

y = (-2/-2) + (4/2)

j = 1 + 2 = 3

De waarde van y bij x = 2 is 3

Voorbeeld 2: Vind de waarde van y bij x = 5 voor de gegeven reeks punten (9, 2), (3, 10)

Oplossing:

Gegeven,

  • (X0, En0) = (9, 2)
  • (X1, En1) = (3, 10)

De Lagrange-interpolatieformule van de eerste orde is:

y~=~frac{(x-x_1)}{(x_0-x_1)} ijden y_0+frac{(x-x_0)}{(x_1-x_0)} ijden y_1

Bij x = 5

y~=~frac{(5-3)}{(9-3)}maal 2+frac{(5-9)}{(3-9)}maal 10

j = (4/6) + (-40/-6)

j = (2/3) + (20/3)

j = 22/3 = 7,33

De waarde van y bij x = 5 is 7,33

Voorbeeld 3: Vind de waarde van y bij x = 1 voor de gegeven reeks punten (1, 6), (3, 4), (2, 5)

Oplossing:

Gegeven,

  • (X0, En0) = (1, 6)
  • (X1, En1) = (3, 4)
  • (X2, En2) = (2, 5)

Lagrange-interpolatieformule van de tweede orde is:

y~=~frac{(x-x_1)(x-x_2)}{(x_0-x_1)(x_0-x_2)} imes y_0+frac{(x-x_0)(x-x_2)}{(x_1 -x_0)(x_1-x_2)} ijden y_1+frac{(x-x_0)(x-x_1)}{(x_2-x_0)(x_2-x_1)} ijden y_2

Bij x = 1

y~=~frac{(1-3)(1-2)}{(1-3)(1-2)} imes 6+frac{(1-1)(1-2)}{( 3-1)(3-2)}maal 4+frac{(1-1)(1-3)}{(2-1)(2-3)}maal 5 y~=~ frac{(-2)(-1)}{(-2)(-1)}maal 6+frac{(0)(-1)}{(2)(1)}maal 4+frac {(0)(-2)}{(1)(-1)}maal 5

j = (12/2) + 0 + 0

j = 6

De waarde van y bij x = 1 is 6

Voorbeeld 4: Vind de waarde van y bij x = 10 voor de gegeven reeks punten (9, 6), (3, 5), (1, 12)

Oplossing:

Gegeven,

  • (X0, En0) = (9, 6)
  • (X1, En1) = (3, 5)
  • (X2, En2) = (1, 12)

Lagrange-interpolatieformule van de tweede orde is:

y~=~frac{(x-x_1)(x-x_2)}{(x_0-x_1)(x_0-x_2)} imes y_0+frac{(x-x_0)(x-x_2)}{(x_1 -x_0)(x_1-x_2)} ijden y_1+frac{(x-x_0)(x-x_1)}{(x_2-x_0)(x_2-x_1)} ijden y_2

Bij x = 10

y~=~frac{(10-3)(10-1)}{(9-3)(9-1)} imes 6+frac{(10-9)(10-1)}{( 3-9)(3-1)}maal 5+frac{(10-9)(10-3)}{(1-9)(1-3)}maal 12 y~=~ frac{(7)(9)}{(6)(8)}maal 6+frac{(1)(9)}{(-6)(2)}maal 5+frac{(1) (7)}{(-8)(-2)}maal 12

j = (63/8) + (-15/4) + (21/4)

y = (63-30 + 42)/8

j = 75/8 = 9,375

De waarde van y bij x = 10 is 9,375

reis maar

Voorbeeld 5: Vind de waarde van y bij x = 7 voor de gegeven reeks punten (1, 10), (2, 4), (3, 4), (5, 7)

Oplossing:

Gegeven,

  • (X0, En0) = (1, 10)
  • (X1, En1) = (2, 4)
  • (X2, En2) = (3, 4)
  • (X3, En3) = (5, 7)

Lagrange-interpolatieformule van de derde orde is:

y~=~frac{(x-x_1)(x-x_2)(x-x_3)}{(x_0-x_1)(x_0-x_2)(x_0-x_3)} ijden y_0+frac{(x-x_0 )(x-x_2)(x-x_3)}{(x_1-x_0)(x_1-x_2)(x_1-x_3)}maal y_1+frac{(x-x_0)(x-x_1)(x-x_3) }{(x_2-x_0)(x_2-x_1)(x_2-x_3)} imes y_2+frac{(x-x_0)(x-x_1)(x-x_2)}{(x_3-x_0)(x_3-x_1 )(x_3-x_2)}maal y_3

Bij x = 7

y~=~frac{(7-2)(7-3)(7-5)}{(1-2)(1-3)(1-5)}maal 10+frac{(7- 1)(7-3)(7-5)}{(2-1)(2-3)(2-5)} imes 4+frac{(7-1)(7-2)(7- 5)}{(3-1)(3-2)(3-5)}maal 4+frac{(7-1)(7-2)(7-3)}{(5-1)( 5-2)(5-3)}maal 7 y~=~frac{(5)(4)(2)}{(-1)(-2)(-4)}maal 10+ frac{(6)(4)(2)}{(1)(-1)(-3)} imes 4+frac{(6)(5)(2)}{(2)(1) (-2)}maal 4+frac{(6)(5)(4)}{(4)(3)(2)}maal 7

j = -50 + 64 – 60 + 35

j = 99 – 110 = -elf

De waarde van y bij x = 7 is -11

Voorbeeld 6: Vind de waarde van y bij x = 10 voor de gegeven reeks punten (5, 12), (6, 13), (7, 14), (8, 15)

Oplossing:

Gegeven,

  • (X0, En0) = (5, 12)
  • (X1, En1) = (6, 13)
  • (X2, En2) = (7, 14)
  • (X3, En3) = (8, 15)

Lagrange-interpolatieformule van de derde orde is:

y~=~frac{(x-x_1)(x-x_2)(x-x_3)}{(x_0-x_1)(x_0-x_2)(x_0-x_3)} ijden y_0+frac{(x-x_0 )(x-x_2)(x-x_3)}{(x_1-x_0)(x_1-x_2)(x_1-x_3)}maal y_1+frac{(x-x_0)(x-x_1)(x-x_3) }{(x_2-x_0)(x_2-x_1)(x_2-x_3)} imes y_2+frac{(x-x_0)(x-x_1)(x-x_2)}{(x_3-x_0)(x_3-x_1 )(x_3-x_2)}maal y_3

Bij x = 10,

y~=~frac{(10-6)(10-7)(10-8)}{(5-6)(5-7)(5-8)} imes 12+frac{(10- 5)(10-7)(10-8)}{(6-5)(6-7)(6-8)} imes 13+frac{(10-5)(10-6)(10- 8)}{(7-5)(7-6)(7-8)}maal 14+frac{(10-5)(10-6)(10-7)}{(8-5)( 8-6)(8-7)}maal 15 y~=~frac{(4)(3)(2)}{(-1)(-2)(-3)}maal 12+ frac{(5)(3)(2)}{(1)(-1)(-2)} imes 13+frac{(5)(4)(2)}{(2)(1) (-1)}maal 14+frac{(5)(4)(3)}{(3)(2)(1)}maal 15

j = -48 + 195 – 280 + 150

j = 17

De waarde van y bij x = 10 is 17

Voorbeeld 7: Vind de waarde van y bij x = 0 voor de gegeven reeks punten (-2, 5),(1, 7)

Oplossing:

Gegeven,

  • (X0, En0) = (-2, 5)
  • (X1, En1) = (1, 7)

Lagrange-interpolatieformule van de eerste orde is:

y~=~frac{(x-x_1)}{(x_0-x_1)} ijden y_0+frac{(x-x_0)}{(x_1-x_0)} ijden y_1

Bij x = 0,

y~=~frac{(0-1)}{(-2-1)}maal 5+frac{(0+2)}{(1+2)}maal 7

j = (5/3) + (14/3)

j = 19/3 = 6,33

De waarde van y bij x = 0 is 6,33

Veelgestelde vragen over de Lagrange-interpolatieformule

1. Wat is de Lagrange-interpolatieformule?

Lagrange-interpolatieformule is een formule die wordt gebruikt om de waarde van de afhankelijke variabele van de functie voor elke onafhankelijke variabele te vinden, ook al is de functie zelf niet gegeven.

2. Wat zijn de toepassingen van de Lagrange-interpolatieformule?

Lagranges Formula heeft verschillende toepassingen in de moderne wiskunde en datawetenschappen,

stad in uas
  • Het wordt gebruikt voor AI-model Traning.
  • Het wordt gebruikt bij beeldverwerking.
  • Het wordt gebruikt bij het tekenen van 3D- en hogere curven, enz.

3. Wat is de Lagrange-interpolatieformule van de eerste orde?

De Lagranges-interpolatieformule van de eerste orde is:

f(x) = (x – x 1 )/(X 0 - X 1 )×v 0 + (x – x 0 )/(X 1 - X 0 )×v 1

4. Wat is de Lagrange-interpolatieformule van de tweede orde?

De Lagranges-interpolatieformule van de tweede orde is:

f(x) = [(x – x 1 )(x – x 2 )/(X 0 - X 1 )(X 0 - X 2 )]×v 0 + [(x – x 0 )(x – x 2 )/(X 1 - X 0 )(X 1 - X 2 )]×v 1 + [(x – x 0 )(x – x 1 )/(X 2 - X 0 )(X 2 - X 2 )]×v 0