De verwijderfunctie wordt gebruikt om het opgegeven knooppunt uit een binaire zoekboom te verwijderen. We moeten echter een knooppunt uit een binaire zoekboom op zo'n manier verwijderen dat de eigenschap van de binaire zoekboom niet wordt geschonden. Er zijn drie situaties waarin een knooppunt uit de binaire zoekboom wordt verwijderd.
Het knooppunt dat moet worden verwijderd, is een bladknooppunt
Het is het eenvoudigste geval. In dit geval vervangt u het bladknooppunt door de NULL en maakt u eenvoudigweg de toegewezen ruimte vrij.
math.random java
In de volgende afbeelding verwijderen we knooppunt 85, omdat het knooppunt een bladknooppunt is. Daarom wordt het knooppunt vervangen door NULL en wordt de toegewezen ruimte vrijgemaakt.
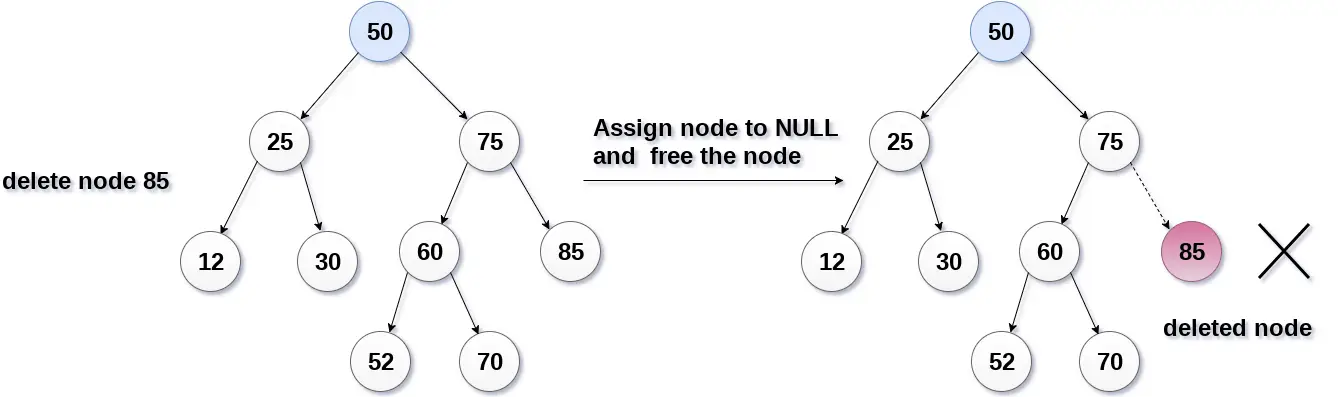
Het knooppunt dat moet worden verwijderd, heeft slechts één kind.
Vervang in dit geval het knooppunt door het onderliggende knooppunt en verwijder het onderliggende knooppunt, dat nu de waarde bevat die moet worden verwijderd. Vervang het eenvoudig door de NULL en maak de toegewezen ruimte vrij.
In de volgende afbeelding moet knooppunt 12 worden verwijderd. Het heeft slechts één kind. Het knooppunt wordt vervangen door het onderliggende knooppunt en het vervangen knooppunt 12 (dat nu het bladknooppunt is) wordt eenvoudigweg verwijderd.

Het te verwijderen knooppunt heeft twee kinderen.
Het is een beetje ingewikkelde zaak vergeleken met de andere twee gevallen. Het knooppunt dat moet worden verwijderd, wordt echter recursief vervangen door zijn opvolger of voorganger in de juiste volgorde totdat de knooppuntwaarde (die moet worden verwijderd) op het blad van de boom wordt geplaatst. Vervang na de procedure het knooppunt door NULL en maak de toegewezen ruimte vrij.
In de volgende afbeelding moet knooppunt 50 worden verwijderd, wat het hoofdknooppunt van de boom is. De onderstaande doorloop van de boom in volgorde.
6, 25, 30, 50, 52, 60, 70, 75.
doorhaling van de afwaardering
vervang 50 door zijn opvolger 52 in de juiste volgorde. Nu wordt 50 verplaatst naar het blad van de boom, dat eenvoudigweg wordt verwijderd.

Algoritme
Verwijderen (BOOM, ITEM)
Schrijf 'item niet gevonden in de boom' ANDERS ALS ITEM DATA
Verwijderen(BOOM->LINKS, ITEM)
ANDERS ALS ITEM > BOOM -> GEGEVENS
Verwijderen(BOOM -> RECHTS, ITEM)
ANDERS ALS BOOM -> LINKS EN BOOM -> RECHTS
SET TEMP = findLargestNode(BOOM -> LINKS)
STEL BOOM IN -> DATA = TEMP -> DATA
Verwijderen(BOOM -> LINKS, TEMP -> DATA)
ANDERS
SET TEMP = BOOM
ALS BOOM -> LINKS = NULL EN BOOM -> RECHTS = NULL
BOOM INSTELLEN = NUL
ANDERS ALS BOOM -> LINKS != NULL
ZET BOOM = BOOM -> LINKS
ANDERS
ZET BOOM = BOOM -> RECHTS
[EIND VAN ALS]
VRIJE TEMP
[EIND VAN ALS]
Functie:
void deletion(Node*& root, int item) { Node* parent = NULL; Node* cur = root; search(cur, item, parent); if (cur == NULL) return; if (cur->left == NULL && cur->right == NULL) { if (cur != root) { if (parent->left == cur) parent->left = NULL; else parent->right = NULL; } else root = NULL; free(cur); } else if (cur->left && cur->right) { Node* succ = findMinimum(cur- >right); int val = succ->data; deletion(root, succ->data); cur->data = val; } else { Node* child = (cur->left)? Cur- >left: cur->right; if (cur != root) { if (cur == parent->left) parent->left = child; else parent->right = child; } else root = child; free(cur); } } Node* findMinimum(Node* cur) { while(cur->left != NULL) { cur = cur->left; } return cur; } 