A Min-hoop wordt gedefinieerd als een soort De heap-gegevensstructuur is een soort binaire boom die in de informatica vaak wordt gebruikt voor verschillende doeleinden, waaronder het sorteren, zoeken en organiseren van gegevens.
Inleiding tot Min-Heap – Tutorials voor gegevensstructuur en algoritmen
Doel en gebruiksscenario's van Min-Heap:
- Prioriteitswachtrij implementeren: Een van de belangrijkste toepassingen van de heap-gegevensstructuur is het implementeren van prioriteitswachtrijen.
- Het algoritme van Dijkstra : Het algoritme van Dijkstra is een kortste-pad-algoritme dat het kortste pad tussen twee knooppunten in een grafiek vindt. Een min heap kan worden gebruikt om de niet-bezochte knooppunten met de kleinste afstand tot het bronknooppunt bij te houden.
- Sorteren: Een min heap kan worden gebruikt als sorteeralgoritme om een verzameling elementen efficiënt in oplopende volgorde te sorteren.
- Mediane bevinding: Een min-heap kan worden gebruikt om efficiënt de mediaan van een stroom getallen te vinden. We kunnen één minimale heap gebruiken om de grotere helft van de getallen op te slaan en één maximale heap om de kleinere helft op te slaan. De mediaan is de wortel van de min-heap.
Min-Heap-gegevensstructuur in verschillende talen:
1. Min-heap in C++
Een min-heap kan worden geïmplementeerd met behulp van de prioriteits-rij container uit de standaardsjabloonbibliotheek (STL). De prioriteits-rij container is een type containeradapter die een manier biedt om elementen op te slaan in een wachtrij-achtige gegevensstructuur waarin aan elk element een prioriteit is gekoppeld.
Syntaxis :
C++ priority_queue < int, vector , groter > minH;>
2. Min-heap op Java
In Java kan een min-heap worden geïmplementeerd met behulp van de Prioriteits-rij klasse uit java.util-pakket . De PriorityQueue-klasse is een prioriteitswachtrij die een manier biedt om elementen op te slaan in een wachtrij-achtige gegevensstructuur waarin aan elk element een prioriteit is gekoppeld.
Syntaxis :
Java PriorityQueue minHeap = nieuwe PriorityQueue ();>
3. Min-Heap in Python
In Python kan een min-heap worden geïmplementeerd met behulp van de hoopq module, die functies biedt voor het implementeren van heaps. In het bijzonder de hoopq module biedt een manier om heap-datastructuren te creëren en te manipuleren.
Syntaxis:
tostring-methodePython
heap = [] heapify(heap)>
4. Min-heap in C#
In C# kan een min-heap worden geïmplementeerd met behulp van de PriorityQueue-klasse uit de System.Collections.Generieke naamruimte . De PriorityQueue-klasse is een prioriteitswachtrij die een manier biedt om elementen op te slaan in een wachtrij-achtige gegevensstructuur waarin aan elk element een prioriteit is gekoppeld.
Syntaxis:
C# var minHeap = new PriorityQueue ();>
5. Min-heap in JavaScript
Een min heap is een binaire boom waarin elk knooppunt een waarde heeft die kleiner is dan of gelijk is aan zijn kinderen. In JavaScript kun je een min-heap implementeren met behulp van een array, waarbij het eerste element het hoofdknooppunt vertegenwoordigt, en de onderliggende elementen van een knooppunt op de index i bevinden zich op indices 2i+1 En 2i+2.
Syntaxis:
JavaScript const minHeap = new MinHeap();>
Verschil tussen Min Heap en Max Heap:
|
| Min hoop | Max Hoop |
|---|---|---|
| 1. | In een Min-Heap moet de sleutel die aanwezig is op het hoofdknooppunt kleiner zijn dan of gelijk zijn aan de sleutels die aanwezig zijn op alle onderliggende knooppunten. | In een Max-Heap moet de sleutel die aanwezig is op het hoofdknooppunt groter zijn dan of gelijk zijn aan de sleutels die aanwezig zijn op alle onderliggende knooppunten. |
| 2. | In een Min-Heap is het minimale sleutelelement aanwezig in de root. | In een Max-Heap is het maximale sleutelelement aanwezig in de root. |
| 3. | Een Min-Heap gebruikt de oplopende prioriteit. | Een Max-Heap gebruikt de aflopende prioriteit. |
| 4. | Bij de constructie van een Min-Heap heeft het kleinste element prioriteit. | Bij de constructie van een Max-Heap heeft het grootste element prioriteit. |
| 5. java probeer te vangen | In een Min-Heap wordt het kleinste element als eerste uit de hoop gehaald. | In een Max-Heap wordt het grootste element als eerste uit de hoop gehaald. |
Interne implementatie van Min-Heap-gegevensstructuur:
A Min heap wordt doorgaans weergegeven als een array .
- Het hoofdelement bevindt zich op Arr[0] .
- Voor elk it-knooppunt Arr[ik] :
- Arr[(i -1) / 2] retourneert het bovenliggende knooppunt.
- Arr[(2 * ik) + 1] retourneert het linker kindknooppunt.
- Arr[(2 * ik) + 2] retourneert het rechter onderliggende knooppunt.
De interne implementatie van de Min-Heap vereist 3 belangrijke stappen:
actress zeenat aman
- Plaatsing : Om een element in de min heap in te voegen, voegen we het element eerst aan het einde van de array toe en passen vervolgens de heap-eigenschap aan door het element herhaaldelijk met zijn ouder te verwisselen totdat het op de juiste positie staat.
- Verwijdering : Om het minimumelement uit de min heap te verwijderen, verwisselen we eerst het rootknooppunt met het laatste element in de array, verwijderen we het laatste element en passen we vervolgens de heap-eigenschap aan door het element herhaaldelijk met zijn kleinste kind te verwisselen totdat het in de juiste positie.
- Heapify : Een heapify-bewerking kan worden gebruikt om een min-heap te maken van een ongesorteerde array.
Bewerkingen op de Min-heap-gegevensstructuur en hun implementatie:
Hier zijn enkele algemene bewerkingen die kunnen worden uitgevoerd op een heap-gegevensstructuur:
1. Invoeging in Min-Heap-gegevensstructuur :
Elementen kunnen in de heap worden ingevoegd volgens een vergelijkbare aanpak als hierboven besproken voor verwijdering. Het idee is om:
- De invoegbewerking in een min-heap omvat de volgende stappen:
- Voeg het nieuwe element toe aan het einde van de hoop, op de volgende beschikbare positie in het laatste niveau van de boom.
- Vergelijk het nieuwe element met het bovenliggende element. Als het bovenliggende element groter is dan het nieuwe element, verwisselt u deze.
- Herhaal stap 2 totdat het bovenliggende element kleiner is dan of gelijk is aan het nieuwe element, of totdat het nieuwe element de wortel van de boom bereikt.
- Het nieuwe element bevindt zich nu op de juiste positie in de min heap en er is voldaan aan de heap-eigenschap.
Illustratie:
Stel dat de heap een min-heap is, als:
Inbrengen in Min-Heap
Implementatie van invoegoperatie in Min-Heap:
C++ #include #include using namespace std; // Function to insert a new element into the min-heap void insert_min_heap(vector & heap, int value) {// Voeg het nieuwe element toe aan het einde van de heap heap.push_back(value); // Haal de index van het laatste element op int index = heap.size() - 1; // Vergelijk het nieuwe element met zijn ouder en wissel indien // nodig while (index> 0 && heap[(index - 1) / 2]> heap[index]) { swap(heap[index], heap[(index - 1) / 2]); // Ga omhoog in de boom naar de ouder van de huidige // elementindex = (index - 1) / 2; } } // Hoofdfunctie om de functie insert_min_heap int main() { vector hoop; int-waarden[] = { 10, 7, 11, 5, 4, 13 }; int n = groottevan(waarden) / groottevan(waarden[0]); voor (int i = 0; ik< n; i++) { insert_min_heap(heap, values[i]); cout << 'Inserted ' << values[i] << ' into the min-heap: '; for (int j = 0; j < heap.size(); j++) { cout << heap[j] << ' '; } cout << endl; } return 0; }>
Java import java.util.*; public class GFG { // Function to insert a new element into the min-heap public static void insertMinHeap(int[] heap, int size, int value) { // Add the new element to the end of the heap heap[size] = value; // Get the index of the last element int index = size; // Compare the new element with its parent and swap // if necessary while (index>0 && heap[(index - 1) / 2]> heap[index]) { swap(heap, index, (index - 1) / 2); // Ga omhoog in de boom naar de ouder van de huidige // elementindex = (index - 1) / 2; } } // Functie om twee elementen in een array te verwisselen public static void swap(int[] arr, int i, int j) { int temp = arr[i]; arr[i] = arr[j]; arr[j] = temperatuur; } // Hoofdfunctie om de functie insertMinHeap te testen public static void main(String[] args) { int[] heap = new int[6]; int[] waarden = { 10, 7, 11, 5, 4, 13 }; int-grootte = 0; voor (int i = 0; ik< values.length; i++) { insertMinHeap(heap, size, values[i]); size++; System.out.print('Inserted ' + values[i] + ' into the min-heap: '); for (int j = 0; j < size; j++) { System.out.print(heap[j] + ' '); } System.out.println(); } } }> Python3 def insert_min_heap(heap, value): # Add the new element to the end of the heap heap.append(value) # Get the index of the last element index = len(heap) - 1 # Compare the new element with its parent and swap if necessary while index>0 en heap[(index - 1) // 2]> heap[index]: heap[index], heap[(index - 1) // 2] = heap[(index - 1) // 2], heap[ index] # Ga omhoog in de boomstructuur naar het bovenliggende element van het huidige element index = (index - 1) // 2 heap = [] waarden = [10, 7, 11, 5, 4, 13] voor waarde in waarden: insert_min_heap( heap, waarde) print(f'Ingevoegde {waarde} in de min-heap: {heap}')> C# using System; using System.Collections.Generic; public class Program { // Function to insert a new element into the min-heap static void InsertMinHeap(List heap, int value) {// Voeg het nieuwe element toe aan het einde van de heap heap.Add(value); // Haal de index van het laatste element op int index = heap.Count - 1; // Vergelijk het nieuwe element met zijn ouder en wissel // indien nodig while (index> 0 && heap[(index - 1) / 2]> heap[index]) { int temp = heap[index]; heap[index] = heap[(index - 1) / 2]; heap[(index - 1) / 2] = temperatuur; // Ga omhoog in de boom naar de ouder van het huidige // element index = (index - 1) / 2; } } // Hoofdfunctie om de InsertMinHeap-functie te testen public static void Main() { List heap = nieuwe lijst (); int[] waarden = { 10, 7, 11, 5, 4, 13 }; foreach(int-waarde in waarden) { InsertMinHeap(heap, waarde); Console.Write('Ingevoegd' + waarde + ' in de min-heap: '); foreach(int-element in heap) { Console.Write(element + ' '); } Console.WriteLine(); } } }> Javascript function insertMinHeap(heap, value) { heap.push(value); let index = heap.length - 1; let parentIndex = Math.floor((index - 1) / 2); while (index>0 && heap[parentIndex]> heap[index]) { [heap[index], heap[parentIndex]] = [heap[parentIndex], heap[index]]; index = ouderIndex; parentIndex = Math.floor((index - 1) / 2); } } // Voorbeeldgebruik const heap = []; const-waarden = [10, 7, 11, 5, 4, 13]; for (const waarde van waarden) { insertMinHeap(heap, waarde); console.log(`${value} ingevoegd in de min-heap: ${heap}`); }> Uitvoer
Inserted 10 into the min-heap: 10 Inserted 7 into the min-heap: 7 10 Inserted 11 into the min-heap: 7 10 11 Inserted 5 into the min-heap: 5 7 11 10 Inserted 4 into the min-heap: 4 5 11 10 7 Inser...>
Tijdcomplexiteit: O(log(n)) ( waarbij n het aantal elementen in de heap is )
Hulpruimte: Op)
2. Verwijdering in Min-Heap-gegevensstructuur :
Het kleinste element (de root) verwijderen uit de min-heap. De root wordt vervangen door het laatste element in de heap, en vervolgens wordt de heap-eigenschap hersteld door de nieuwe root te verwisselen met het kleinste kind totdat de ouder kleiner is dan beide kinderen of totdat de nieuwe root een bladknooppunt bereikt.
- Vervang de root of het element dat moet worden verwijderd door het laatste element.
- Verwijder het laatste element uit de heap.
- Omdat het laatste element nu op de positie van het rootknooppunt wordt geplaatst. Het volgt dus mogelijk niet de heap-eigenschap. Heap daarom het laatste knooppunt op dat op de positie van de wortel is geplaatst.
Illustratie :
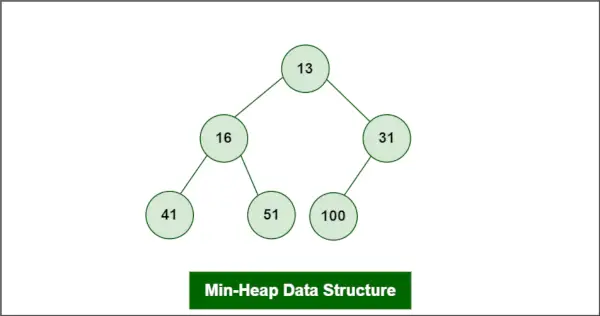
Stel dat de heap een min-heap is, als:
Min-Heap-gegevensstructuur
Het te verwijderen element is root, d.w.z. 13.
Proces :
Het laatste element is 100.
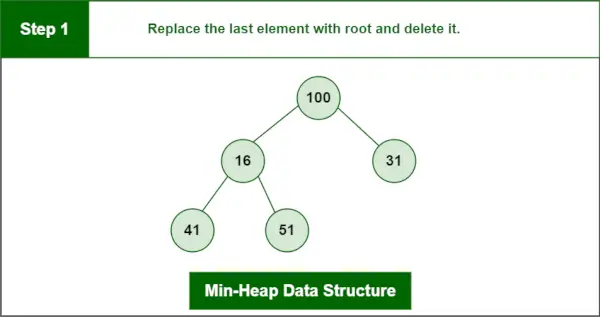
Stap 1: Vervang het laatste element door root en verwijder het.
Min-Heap-gegevensstructuur
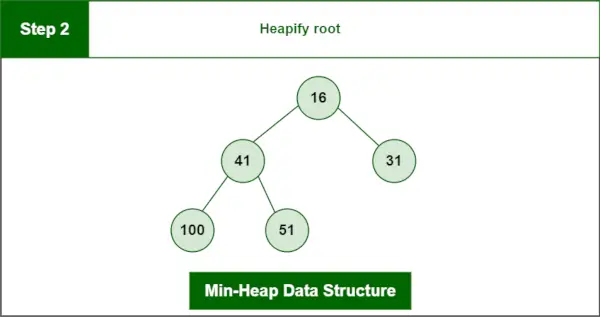
Stap 2 : Heapify-wortel.
Laatste hoop:
Min-Heap-gegevensstructuur
Implementatie van verwijderingsbewerking in Min-Heap:
C++ #include #include using namespace std; // Function to insert a new element into the min-heap void insert_min_heap(vector & heap, int value) {// Voeg het nieuwe element toe aan het einde van de heap heap.push_back(value); // Haal de index van het laatste element op int index = heap.size() - 1; // Vergelijk het nieuwe element met zijn ouder en wissel indien // nodig while (index> 0 && heap[(index - 1) / 2]> heap[index]) { swap(heap[index], heap[(index - 1) / 2]); // Ga omhoog in de boom naar de ouder van de huidige // elementindex = (index - 1) / 2; } } // Functie om een knooppunt uit de min-heap void delete_min_heap(vector & heap, int value) {// Zoek de index van het element dat moet worden verwijderd int index = -1; voor (int i = 0; ik< heap.size(); i++) { if (heap[i] == value) { index = i; break; } } // If the element is not found, return if (index == -1) { return; } // Replace the element to be deleted with the last // element heap[index] = heap[heap.size() - 1]; // Remove the last element heap.pop_back(); // Heapify the tree starting from the element at the // deleted index while (true) { int left_child = 2 * index + 1; int right_child = 2 * index + 2; int smallest = index; if (left_child < heap.size() && heap[left_child] < heap[smallest]) { smallest = left_child; } if (right_child < heap.size() && heap[right_child] < heap[smallest]) { smallest = right_child; } if (smallest != index) { swap(heap[index], heap[smallest]); index = smallest; } else { break; } } } // Main function to test the insert_min_heap and // delete_min_heap functions int main() { vector hoop; int-waarden[] = { 13, 16, 31, 41, 51, 100 }; int n = groottevan(waarden) / groottevan(waarden[0]); voor (int i = 0; ik< n; i++) { insert_min_heap(heap, values[i]); } cout << 'Initial heap: '; for (int j = 0; j < heap.size(); j++) { cout << heap[j] << ' '; } cout << endl; delete_min_heap(heap, 13); cout << 'Heap after deleting 13: '; for (int j = 0; j < heap.size(); j++) { cout << heap[j] << ' '; } cout << endl; return 0; }>
Java import java.util.*; public class GFG { // Function to insert a new element into the min-heap public static void insertMinHeap(List heap, int value) {// Voeg het nieuwe element toe aan het einde van de heap heap.add(value); // Haal de index van het laatste element op int index = heap.size() - 1; // Vergelijk het nieuwe element met zijn ouder en ruil // indien nodig while (index> 0 && heap.get((index - 1) / 2)> heap.get(index)) { Collections.swap(heap, index, (index - 1) / 2); // Ga omhoog in de boom naar de ouder van de huidige // elementindex = (index - 1) / 2; } } // Functie om een knooppunt te verwijderen uit de min-heap public static void deleteMinHeap(List heap, int value) {// Zoek de index van het element dat moet worden verwijderd int index = -1; voor (int i = 0; ik< heap.size(); i++) { if (heap.get(i) == value) { index = i; break; } } // If the element is not found, return if (index == -1) { return; } // Replace the element to be deleted with the last // element heap.set(index, heap.get(heap.size() - 1)); // Remove the last element heap.remove(heap.size() - 1); // Heapify the tree starting from the element at the // deleted index while (true) { int leftChild = 2 * index + 1; int rightChild = 2 * index + 2; int smallest = index; if (leftChild < heap.size() && heap.get(leftChild) < heap.get(smallest)) { smallest = leftChild; } if (rightChild < heap.size() && heap.get(rightChild) < heap.get(smallest)) { smallest = rightChild; } if (smallest != index) { Collections.swap(heap, index, smallest); index = smallest; } else { break; } } } // Main function to test the insertMinHeap and // deleteMinHeap functions public static void main(String[] args) { List heap = nieuwe ArrayList (); int[] waarden = { 13, 16, 31, 41, 51, 100 }; int n = waarden.lengte; voor (int i = 0; ik< n; i++) { insertMinHeap(heap, values[i]); } System.out.print('Initial heap: '); for (int j = 0; j < heap.size(); j++) { System.out.print(heap.get(j) + ' '); } System.out.println(); deleteMinHeap(heap, 13); System.out.print('Heap after deleting 13: '); for (int j = 0; j < heap.size(); j++) { System.out.print(heap.get(j) + ' '); } System.out.println(); } }> Python3 def insert_min_heap(heap, value): heap.append(value) index = len(heap) - 1 while index>0 en heap[(index - 1) // 2]> heap[index]: heap[index], heap[(index - 1) // 2] = heap[(index - 1) // 2], heap[ index] index = (index - 1) // 2 def delete_min_heap(heap, waarde): index = -1 voor i in bereik(len(heap)): if heap[i] == waarde: index = ik break if index == -1: return heap[index] = heap[-1] heap.pop() while True: left_child = 2 * index + 1 right_child = 2 * index + 2 kleinste = index indien left_child< len(heap) and heap[left_child] < heap[smallest]: smallest = left_child if right_child < len(heap) and heap[right_child] < heap[smallest]: smallest = right_child if smallest != index: heap[index], heap[smallest] = heap[smallest], heap[index] index = smallest else: break heap = [] values = [13, 16, 31, 41, 51, 100] for value in values: insert_min_heap(heap, value) print('Initial heap:', heap) delete_min_heap(heap, 13) print('Heap after deleting 13:', heap)> C# using System; using System.Collections.Generic; class MinHeap { private List heap = nieuwe lijst (); public void Insert(int-waarde) { heap.Add(waarde); int index = heap.Count - 1; while (index> 0 && heap[(index - 1) / 2]> heap[index]) { Swap(index, (index - 1) / 2); index = (index - 1) / 2; } } public void Verwijderen(int waarde) { int index = heap.IndexOf(waarde); als (index == -1) { return; } heap[index] = heap[heap.Count - 1]; heap.RemoveAt(heap.Count - 1); terwijl (waar) { int leftChild = 2 * index + 1; int rechtsKind = 2 * index + 2; int kleinste = index; if (linkskind< heap.Count && heap[leftChild] < heap[smallest]) { smallest = leftChild; } if (rightChild < heap.Count && heap[rightChild] < heap[smallest]) { smallest = rightChild; } if (smallest != index) { Swap(index, smallest); index = smallest; } else { break; } } } private void Swap(int i, int j) { int temp = heap[i]; heap[i] = heap[j]; heap[j] = temp; } public void Print() { for (int i = 0; i < heap.Count; i++) { Console.Write(heap[i] + ' '); } Console.WriteLine(); } } class Program { static void Main(string[] args) { MinHeap heap = new MinHeap(); int[] values = { 13, 16, 31, 41, 51, 100 }; for (int i = 0; i < values.Length; i++) { heap.Insert(values[i]); } Console.Write('Initial heap: '); heap.Print(); heap.Delete(13); Console.Write('Heap after deleting 13: '); heap.Print(); } }> Javascript function insertMinHeap(heap, value) { // Add the new element to the end of the heap heap.push(value); // Get the index of the last element let index = heap.length - 1; // Compare the new element with its parent and swap if necessary for (let flr = Math.floor((index - 1) / 2); index>0 && heap[flr]> heap[index]; flr = Math.floor((index - 1) / 2)) { [heap[index], heap[flr]] = [heap[flr], heap[index], ]; // Ga omhoog in de boomstructuur naar het bovenliggende element van de huidige elementindex = Math.floor((index - 1) / 2); } } function deleteMinHeap(heap, value) {// Zoek de index van het element dat moet worden verwijderd, let index = -1; voor (laat i = 0; i< heap.length; i++) { if (heap[i] == value) { index = i; break; } } // If the element is not found, return if (index == -1) { return; } // Replace the element to be deleted with the last element heap[index] = heap[heap.length - 1]; // Remove the last element heap.pop(); // Heapify the tree starting from the element at the deleted index while (true) { let left_child = 2 * index + 1; let right_child = 2 * index + 2; let smallest = index; if (left_child < heap.length && heap[left_child] < heap[smallest]) { smallest = left_child; } if (right_child < heap.length && heap[right_child] < heap[smallest]) { smallest = right_child; } if (smallest != index) { [heap[index], heap[smallest]] = [heap[smallest], heap[index]]; index = smallest; } else { break; } } } // Main function to test the insertMinHeap and deleteMinHeap functions let heap = []; let values = [13, 16, 31, 41, 51, 100]; for (let i = 0; i < values.length; i++) { insertMinHeap(heap, values[i]); } console.log('Initial heap: ' + heap.join(' ')); deleteMinHeap(heap, 13); console.log('Heap after deleting 13: ' + heap.join(' '));> Uitvoer
Initial heap: 13 16 31 41 51 100 Heap after deleting 13: 16 41 31 100 51>
Tijdcomplexiteit : O(log n) waarbij n het aantal elementen in de heap is
Hulpruimte: Op)
3. Kijkoperatie op Min-Heap-gegevensstructuur:
Om toegang te krijgen tot het minimumelement (d.w.z. de root van de heap), wordt de waarde van het rootknooppunt geretourneerd. De tijdscomplexiteit van kijkje in een min-heap is O(1).
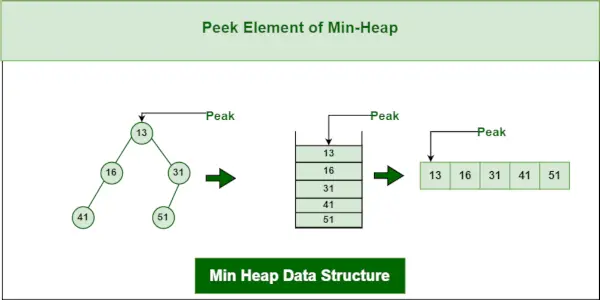
Min Heap-gegevensstructuur
Implementatie van Peek-bewerking in Min-Heap:
C++ #include #include #include using namespace std; int main() { // Create a max heap with some elements using a // priority_queue priority_queue , groter > minHeap; minHeap.push(9); minHeap.push(8); minHeap.push(7); minHeap.push(6); minHeap.push(5); minHeap.push(4); minHeap.push(3); minHeap.push(2); minHeap.push(1); // Haal het peak-element op (d.w.z. het grootste element) int peakElement = minHeap.top(); // Druk het piekelement af<< 'Peak element: ' << peakElement << std::endl; return 0; }> Java import java.util.PriorityQueue; public class GFG { public static void main(String[] args) { // Create a max heap with some elements using a // PriorityQueue PriorityQueue minHeap = nieuwe PriorityQueue(); minHeap.add(9); minHeap.add(8); minHeap.add(7); minHeap.add(6); minHeap.add(5); minHeap.add(4); minHeap.add(3); minHeap.add(2); minHeap.add(1); // Haal het peak-element op (d.w.z. het grootste element) int peakElement = minHeap.peek(); // Druk het peak-element System.out.println('Peak element: ' + peakElement) af; } }> Python3 import heapq # Create a min heap with some elements using a list min_heap = [9, 8, 7, 6, 5, 4, 3, 2, 1] heapq.heapify(min_heap) # Get the peak element (i.e., the smallest element) peak_element = heapq.nsmallest(1, min_heap)[0] # Print the peak element print('Peak element:', peak_element)> C# using System; using System.Collections.Generic; public class GFG { public static void Main() { // Create a min heap with some elements using a // PriorityQueue var minHeap = new PriorityQueue (); minHeap.Enqueue(9); minHeap.Enqueue(8); minHeap.Enqueue(7); minHeap.Enqueue(6); minHeap.Enqueue(5); minHeap.Enqueue(4); minHeap.Enqueue(3); minHeap.Enqueue(2); minHeap.Enqueue(1); // Haal het peak-element op (d.w.z. het kleinste element) int peakElement = minHeap.Peek(); // Druk het peak-element Console.WriteLine('Peak element: ' + peakElement) af; } }> Javascript const PriorityQueue = require('fast-priority-queue'); // Create a min heap with some elements using a PriorityQueue const minHeap = new PriorityQueue((a, b) =>a - b); minHeap.add(9); minHeap.add(8); minHeap.add(7); minHeap.add(6); minHeap.add(5); minHeap.add(4); minHeap.add(3); minHeap.add(2); minHeap.add(1); // Haal het peak-element op (d.w.z. het kleinste element) const peakElement = minHeap.peek(); // Druk het peak-element console.log(`Peak element: ${peakElement}`) af;> Uitvoer
Peak element: 1>
Tijdcomplexiteit : In een min-heap die is geïmplementeerd met behulp van een array of een lijst, is het peak-element in constante tijd toegankelijk, O(1), omdat het zich altijd in de root van de heap bevindt.
In een min heap die is geïmplementeerd met behulp van een binaire boom, is het peak-element ook toegankelijk in O(1) tijd, omdat het zich altijd aan de wortel van de boom bevindt.
Hulpruimte: Op)
4. Heapify-bewerking op Min-Heap-gegevensstructuur:
Een heapify-bewerking kan worden gebruikt om een min-heap te maken van een ongesorteerde array. Dit wordt gedaan door te beginnen bij het laatste niet-bladknooppunt en herhaaldelijk de bubble-down-operatie uit te voeren totdat alle knooppunten voldoen aan de heap-eigenschap.
Heapify-bewerking in Min Heap
Implementatie van Heapify-bewerking in Min-Heap:
C++ #include #include using namespace std; void minHeapify(vector &arr, int i, int n) { int kleinste = i; int l = 2*i + 1; int r = 2*i + 2; als (l< n && arr[l] < arr[smallest]) smallest = l; if (r < n && arr[r] < arr[smallest]) smallest = r; if (smallest != i) { swap(arr[i], arr[smallest]); minHeapify(arr, smallest, n); } } int main() { vector arr = {10, 5, 15, 2, 20, 30}; uit<< 'Original array: '; for (int i = 0; i < arr.size(); i++) cout << arr[i] << ' '; // Perform heapify operation on min-heap for (int i = arr.size()/2 - 1; i>= 0; i--) minHeapify(arr, i, arr.size()); uit<< '
Min-Heap after heapify operation: '; for (int i = 0; i < arr.size(); i++) cout << arr[i] << ' '; return 0; }>
Java // Java code of Heapify operation in Min-Heap import java.util.Arrays; import java.util.List; public class Main { // Function to maintain the min-heap property of the heap rooted at index 'i' public static void minHeapify(List arr, int i, int n) {// Stel dat de wortel het kleinste element is, aanvankelijk int kleinste = i; // Bereken de indices van het linker- en rechterkind van het huidige knooppunt int l = 2 * i + 1; int r = 2 * ik + 2; // Vergelijk het linkerkind met het huidige kleinste als (l< n && arr.get(l) < arr.get(smallest)) smallest = l; // Compare the right child with the current smallest if (r < n && arr.get(r) < arr.get(smallest)) smallest = r; // If the current node is not the smallest, swap it with the smallest child if (smallest != i) { int temp = arr.get(i); arr.set(i, arr.get(smallest)); arr.set(smallest, temp); // Recursively heapify the subtree rooted at the smallest child minHeapify(arr, smallest, n); } } public static void main(String[] args) { // Create a list representing the array List arr = Arrays.asList(10, 5, 15, 2, 20, 30); System.out.print('Originele array: '); // Druk de originele array af voor (int i = 0; i< arr.size(); i++) System.out.print(arr.get(i) + ' '); // Perform heapify operation on the min-heap // Start from the last non-leaf node and go up to the root of the tree for (int i = arr.size() / 2 - 1; i>= 0; i--) minHeapify(arr, i, arr.size()); System.out.print('
Min-Heap na heapify-bewerking: '); // Druk de min-heap af na heapify-bewerking voor (int i = 0; i< arr.size(); i++) System.out.print(arr.get(i) + ' '); } }> Python def minHeapify(arr, i, n): smallest = i left = 2 * i + 1 right = 2 * i + 2 if left < n and arr[left] < arr[smallest]: smallest = left if right < n and arr[right] < arr[smallest]: smallest = right if smallest != i: arr[i], arr[smallest] = arr[smallest], arr[i] minHeapify(arr, smallest, n) if __name__ == '__main__': arr = [10, 5, 15, 2, 20, 30] print('Original array:', arr) # Perform heapify operation on a min-heap for i in range(len(arr) // 2 - 1, -1, -1): minHeapify(arr, i, len(arr)) print('Min-Heap after heapify operation:', arr)> C# using System; using System.Collections.Generic; class GFG { // Function to perform the minHeapify operation on a min-heap. static void MinHeapify(List arr, int i, int n) { int kleinste = i; int links = 2 * ik + 1; int rechts = 2 * ik + 2; // Vergelijk het linkerkind met het huidige kleinste knooppunt. als (links< n && arr[left] < arr[smallest]) smallest = left; // Compare the right child with the current smallest node. if (right < n && arr[right] < arr[smallest]) smallest = right; // If the current node is not the smallest // swap it with the smallest child. if (smallest != i) { int temp = arr[i]; arr[i] = arr[smallest]; arr[smallest] = temp; // Recursively call minHeapify on the affected subtree. MinHeapify(arr, smallest, n); } } static void Main(string[] args) { List arr = nieuwe lijst { 10, 5, 15, 2, 20, 30 }; Console.Write('Originele array: '); foreach (int num in arr) Console.Write(num + ' '); // Voer een heapify-bewerking uit op de min-heap. for (int i = arr.Count / 2 - 1; i>= 0; i--) MinHeapify(arr, i, arr.Count); Console.Write('
Min-Heap na heapify-bewerking: '); foreach (int num in arr) Console.Write(num + ' '); } }> Javascript // Define a function to perform min-heapify operation on an array function minHeapify(arr, i, n) { let smallest = i; let l = 2 * i + 1; let r = 2 * i + 2; // Check if left child is smaller than the current smallest element if (l < n && arr[l] < arr[smallest]) smallest = l; // Check if right child is smaller than the current smallest element if (r < n && arr[r] < arr[smallest]) smallest = r; // If the smallest element is not the current element, swap them if (smallest !== i) { [arr[i], arr[smallest]] = [arr[smallest], arr[i]]; minHeapify(arr, smallest, n); } } // Main function function main() { const arr = [10, 5, 15, 2, 20, 30]; // Print the original array console.log('Original array: ' + arr.join(' ')); // Perform heapify operation on the min-heap for (let i = Math.floor(arr.length / 2) - 1; i>= 0; i--) minHeapify(arr, i, arr.lengte); // Druk de min-heap af na heapify-bewerking console.log('Min-Heap na heapify-bewerking: ' + arr.join(' ')); } // Roep de hoofdfunctie aan om het proces main();> Uitvoer
Original array: 10 5 15 2 20 30 Min-Heap after heapify operation: 2 5 15 10 20 30>
De tijdscomplexiteit van heapify in een min-heap is O(n).
priemgetal in Java
5. Zoekoperatie op Min-Heap-gegevensstructuur:
Om naar een element in de min-heap te zoeken, kan een lineaire zoekopdracht worden uitgevoerd over de array die de heap vertegenwoordigt. De tijdscomplexiteit van een lineaire zoekopdracht is echter O(n), wat niet efficiënt is. Daarom is zoeken geen veelgebruikte bewerking in een min-heap.
Hier is een voorbeeldcode die laat zien hoe u naar een element in een min-heap kunt zoeken met behulp van std::vind() :
C++ #include using namespace std; int main() { priority_queue , groter > min_heap; // voorbeeld max heap min_heap.push(10); min_heap.push(9); min_heap.push(8); min_heap.push(6); min_heap.push(4); int-element = 6; // element om te zoeken naar bool gevonden = false; // Kopieer de min heap naar een tijdelijke wachtrij en zoek naar // het element std::priority_queue , groter > temp = min_heap; while (!temp.empty()) { if (temp.top() == element) { gevonden = waar; pauze; } temp.pop(); } if (gevonden) { std::cout<< 'Element found in the min heap.' << std::endl; } else { std::cout << 'Element not found in the min heap.' << std::endl; } return 0; }> Java import java.util.PriorityQueue; public class GFG { public static void main(String[] args) { PriorityQueue min_heap = nieuwe PriorityQueue(); min_heap.add(3); // voeg elementen in de prioriteitswachtrij min_heap.offer(1); min_heap.offer(4); min_heap.aanbieding(1); min_heap.offer(6); int-element = 6; // element om te zoeken naar boolean gevonden = false; // Kopieer de min heap naar een tijdelijke wachtrij en zoek // naar het element PriorityQueue temp = nieuwe PriorityQueue(min_heap); while (!temp.isEmpty()) { if (temp.poll() == element) { gevonden = waar; pauze; } } if (gevonden) { System.out.println( 'Element gevonden in de min heap.'); } else { System.out.println( 'Element niet gevonden in de minimale heap.'); } } }> Python3 import heapq min_heap = [1, 2, 3, 5, 6, 7, 8, 10] # example min heap heapq.heapify(min_heap) element = 6 # element to search for found = False # Copy the min heap to a temporary list and search for the element temp = list(min_heap) while temp: if heapq.heappop(temp) == element: found = True break if found: print('Element found in the min heap.') else: print('Element not found in the min heap.')> C# using System; using System.Collections.Generic; public class GFG { public static void Main() { var minHeap = new PriorityQueue (); // voorbeeld min heap minHeap.Enqueue(4); minHeap.Enqueue(6); minHeap.Enqueue(8); minHeap.Enqueue(9); minHeap.Enqueue(10); int-element = 6; // element om te zoeken naar bool gevonden = false; // Kopieer de min heap naar een tijdelijke wachtrij en zoek // naar het element var temp = new PriorityQueue (minHeap); while (temp.Count> 0) { if (temp.Peek() == element) { gevonden = waar; pauze; } temp.Dequeue(); } if (gevonden) { Console.WriteLine( 'Element gevonden in de minimale heap.'); } else { Console.WriteLine( 'Element niet gevonden in de minimale heap.'); } } }> Javascript // Example min heap let minHeap = new PriorityQueue(); minHeap.enqueue(4); minHeap.enqueue(6); minHeap.enqueue(8); minHeap.enqueue(9); minHeap.enqueue(10); let element = 6; // Element to search for let found = false; // Copy the min heap to a temporary queue and search for the element let temp = new PriorityQueue(minHeap); while (temp.size()>0) { if (temp.peek() == element) { gevonden = waar; pauze; } temp.dequeue(); } if (gevonden) { console.log('Element gevonden in de min heap.'); } else { console.log('Element niet gevonden in de minimale heap.'); }> Uitvoer
Element found in the min heap.>
Complexiteitsanalyse :
De tijd complexiteit van dit programma is O(n logboek n) , waar N is het aantal elementen in de prioriteitswachtrij.
De invoegoperatie heeft een tijdscomplexiteit van O(logboek n) in het ergste geval omdat de heap-eigenschap behouden moet blijven. De zoekbewerking omvat het kopiëren van de prioriteitswachtrij naar een tijdelijke wachtrij en het vervolgens doorkruisen van de tijdelijke wachtrij O(n logboek n) In het ergste geval duurt het langer, omdat elk element moet worden gekopieerd en uit de wachtrij moet worden gehaald, en de prioriteitswachtrij voor elke bewerking opnieuw moet worden opgebouwd.
De complexiteit van de ruimte van het programma is Op) omdat het opslaat N elementen in de prioriteitswachtrij en creëert een tijdelijke wachtrij N elementen.
Toepassingen van Min-Heap-gegevensstructuur:
- Heap-sortering: Min heap wordt gebruikt als een sleutelcomponent in het heap sorteeralgoritme, een efficiënt sorteeralgoritme met een tijdscomplexiteit van O(nlogn).
- Prioriteits-rij: Een prioriteitswachtrij kan worden geïmplementeerd met behulp van een min-heap-gegevensstructuur waarbij het element met de minimumwaarde altijd in de root staat.
- Dijkstra’s algoritme: In het algoritme van Dijkstra wordt een min heap gebruikt om de hoekpunten van de grafiek op te slaan met de minimale afstand tot het startpunt. Het hoekpunt met de minimale afstand bevindt zich altijd aan de wortel van de hoop.
- Huffman-codering: Bij Huffman-codering wordt een min-heap gebruikt om een prioriteitswachtrij te implementeren om een optimale prefixcode voor een gegeven set tekens te bouwen.
- K-gesorteerde arrays samenvoegen: Gegeven K-gesorteerde arrays, kunnen we ze efficiënt samenvoegen tot een enkele gesorteerde array met behulp van een min-heap-gegevensstructuur.
Voordelen van Min-heap-gegevensstructuur:
- Efficiënt inbrengen en verwijderen : Min heap maakt het snel invoegen en verwijderen van elementen mogelijk met een tijdscomplexiteit van O(log n), waarbij n het aantal elementen in de heap is.
- Efficiënt ophalen van minimaal element: Het minimumelement in een min-heap bevindt zich altijd in de root van de heap, en kan in O(1)-tijd worden opgehaald.
- Ruimtebesparend: Min heap is een compacte datastructuur die kan worden geïmplementeerd met behulp van een array of een binaire boom, waardoor deze ruimte-efficiënt is.
- Sorteren: Min heap kan worden gebruikt om een efficiënt sorteeralgoritme te implementeren, zoals heap sort met een tijdscomplexiteit van O(n log n).
- Prioriteits-rij: Min heap kan worden gebruikt om een prioriteitswachtrij te implementeren, waarbij het element met de minimale prioriteit efficiënt in O(1) tijd kan worden opgehaald.
- Veelzijdigheid: Min heap heeft verschillende toepassingen in de informatica, waaronder grafiekalgoritmen, datacompressie en databasesystemen.
Over het geheel genomen is min heap een nuttige en veelzijdige datastructuur die efficiënte werking en ruimte-efficiëntie biedt en verschillende toepassingen heeft in de informatica.